Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Gebruiker:Franciscus/kladblok
Deelonderwerp
Deze pagina gebruik ik om nieuwe artikelen even op te bergen en te bewerken, vóórdat ik ze als bijdrage op Wikisage zet. Ook kan ik hier enkele geheugensteuntjes kwijt.
Franciscus 4 feb 2009 14:55 (UTC)
Das Glasperlenspiel
Das Glasperlenspiel (nl) (Het kralenspel) is een roman uit 1943 van de Zwitserse schrijver Herman Hesse. Deze roman vormt binnen zijn oeuvre een hoogtepunt, en kan worden beschouwd als zijn magnum opus,waarin het gevecht van de mens tegen de machtswellust wordt weergegeven en wordt afgerekend met dictaturen. Het gaat over de strijd van de mens tegen ideologieën.
Inhoud
Het Kralenspel behoort tot die veelomvattende epische werken, die de problematiek van de Europese beschaving samenvatten. Dit wordt door de schrijver Hermann Hesse tot uitdrukking gebracht in een fictieve biografie van de hoofdpersoon Josef Knecht, die we volgen in zijn opleiding, carrière en intellectuele ontwikkeling in de denkbeeldige staat Kastalië.
Jozef Knecht ( nomen est omen ), die uit een eenvoudige familie stamt, - maar zeer begaafd is - brengt het in deze elite-orde tot een van de hoogste posten, tot Magister Ludi.
Het Kralenspel speelt een belangrijke rol in het leven van de ingezetenen die uit voornamelijk jonge, erudiete mensen bestaat. Waarover het Kralenspel gaat wordt niet precies duidelijk gemaakt. De regels van het spel zijn zo ingewikkeld, dat ze bijna niet zijn uit te leggen. Het spelen vergt dan ook jaren van gedisciplineerde studie van muziek, wiskunde en cultuurgeschiedenis. Het is eigenlijk te beschouwen als een synthese van alle kunsten en studies.
In de inleiding van het boek wordt wel een beschouwing gegeven over de regels, de tekentaal en de grammatica van het Spel. Uitgelegd wordt ook, dat deze geheimtaal in staat is de inhouden en uitkomsten van nagenoeg alle wetenschappen en hun onderlinge relaties tot uitdrukking te brengen. Belangrijk bij het spel is, dat de spelers verbanden vinden tussen onderwerpen die op het eerste gezicht niets met elkaar te maken lijken te hebben.
Eschholz
In de elitescholen van Katalië wordt het contact met de buitenwereld zoveel mogelijk buitengesloten, in het bijzonder politieke kwesties. Deze tegenstrijdigheden zijn het die cruciaal zijn voor het leven van de held, Josef Knecht zijn.
Als jongen wordt hij door de plaatselijke Latijnse school met behulp van de Muziekmeester - één van de hoge oversten - als flos juventutis - ofwel Schuingedrukte tekstelecti1) genoemd - toegewezen en geplaatst op de eliteschool in de staat Kastalia. Het wordt de school van Eschholz: het grootste en het modernste scholencomplex van Kastalië. De school omsloot een rechthoekig plein met vijf bomen in de vorm van een dobbelsteen. Het gebouw zelf werd gedragen door vijf zuilen.
Het getal 5 is hierbij niet geheel toevallig: het symboliseert namelijk:zich een doel stellen, geduld en trouw ontwikkelen.
In Eschholz verandert Josef Knecht wezenlijk door de goede verstandhouding met de muziekmeester, en schikt hij zich volledig in de regels van de Orde.
Meer en meer maakt hij zich de vaardigheden eigen die behoren bij de diepgaande kennis van de wetenschap en de muziek. Na enkele jaren van studie in Eschholz wordt hij met enkele medestudenten overgeplaatst naar Waldzell; het hoogste niveau in de Orde.
Waldzell
1)Uitverkorene
Das Glasperlenspiel (nl) ( Het kralenspel ) is een novelle uit 1943 van de Zwitserse schrijver Herman Hesse. Deze novelle vormt binnen zijn oeuvre een hoogtepunt, en kan worden beschouwd als zijn magnum opus.
Inhoud
Das Glasperlenspiel
Das Glasperlenspiel (nl) (Het kralenspel) is een roman uit 1943 van de Zwitserse schrijver Herman Hesse. Deze roman vormt binnen zijn oeuvre een hoogtepunt, en kan worden beschouwd als zijn magnum opus, waarin het gevecht van de mens tegen de machtswellust wordt weergegeven en wordt afgerekend met dictaturen. Het gaat over de strijd van de mens tegen ideologieën.
Inhoud
Het Kralenspel behoort tot die veelomvattende epische werken, die de problematiek van de Europese beschaving samenvatten. Dit wordt door de schrijver Hermann Hesse tot uitdrukking gebracht in een fictieve biografie van de hoofdpersoon Josef Knecht, die we volgen in zijn opleiding, carrière en intellectuele ontwikkeling in de de denkbeeldige staat Kastalië.
Jozef Knecht (nomen est omen), die uit een eenvoudige familie stamt, - maar zeer begaafd is en nobel van inborst - brengt het in deze elite-orde tot een van de hoogste posten, tot Magister Ludi.
Het Kralenspel speelt een belangrijke rol in het leven van de ingezetenen die uit voornamelijk jonge, erudiete mensen bestaat. Waarover het Kralenspel gaat wordt niet precies duidelijk gemaakt. De regels van het spel zijn zo ingewikkeld, dat ze bijna niet zijn uit te leggen. Het spelen vergt dan ook jaren van gedisciplineerde studie van muziek, wiskunde en cultuurgeschiedenis. Het is eigenlijk te beschouwen als een synthese van alle kunsten en studies.
In de inleiding van het boek wordt hierover wel een beschouwing gegeven over de regels, de tekentaal en de grammatica van het Spel . Gezegd wordt ook, dat deze geheimtaal in staat is de inhouden en uitkomsten van nagenoeg alle wetenschappen en hun onderlinge relaties tot uitdrukking te brengen. Belangrijk bij het spel is, dat de spelers verbanden vinden tussen onderwerpen die op het eerste gezicht niets met elkaar te maken lijken te hebben.
Daarnaast wordt het contact met de buitenwereld zoveel mogelijk buitengesloten, in het bijzonder politieke kwasties. Deze tegenstrijdigheden zijn het die cruciaal zijn voor het leven van de held, Josef Knecht zijn. Als jongen wordt hij van de plaatselijke Latijnse school weggehaald en geplaatst op de eliteschool in de staat Kastalia..Wezenlijk verandert hij door de goede verstandhouding met de muziekmeester – een van de hoge oversten – schikt hij zich volledig in de regels van de Orde.
Meer en meer,maakt hij zich de vaardigheden eigen die behoren bij de diepgaande kennis van de wetenschap de muziek en de meditatie en ten slotte het Kralenspel. Hierdoor stijgt hij steeds hoger in de hiërarchie, totdat het uiteindelijk een van de hoogste rangen bereikt, namelijk die van Magister Ludi.
Het Kralenspel is een utopische roman die het gevecht van de mens tegen de machtswellust weergeeft en afrekent met dictaturen. Het gaat over de strijd van de mens tegen ideologieën.
Het Kralenspel is een utopische roman over een spel, dat alle wetenschap en kunst omvat.
De wereld van een soort monastieke orde speelt zich in de toekomst af in de denkbeeldige staat Kastalië.
Het kralenspel speelt een belangrijke rol in het leven van de ingezetenen die uit voornamelijk jonge mensen bestaat. Waarover het Kralenspel precies gaat wordt nooit geheel duidelijk. De regels van het spel zijn zo ingewikkeld, dat ze bijna niet uit te leggen zijn, laat staan te begrijpen. Het spelen vergt dan ook jaren van gedisciplineerde studie van muziek, wiskunde en cultuurgeschiedenis. Het is eigenlijk te beschouwen als een synthese van alle kunsten en studies. Het spel gaat over verschillende werelden en tijden.
Belangrijk bij het spel is, dat de spelers verbanden vinden tussen onderwerpen die op het eerste gezicht niets met elkaar te maken lijken te hebben.
De hoofdpersoon van deze novelle - Jozef Knecht - voert ons door de
{{Overline| (12)}}om ergens een lijntje boven te trekken{{Overline|24}}
12
24
12
--
24
Breuken
a b⁄c: a b/c (geheel getal, teller en noemer) a⁄b: a/b (teller en noemer) 1⁄a: 1/a (alleen noemer)
12
--
24
{{Overline|24}}
12
24
44
sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = sin 32,3122 0 = 0,5345
24
- <math>\tfrac {1}{10} = \tfrac {1}{10^1} = 0{,}1</math> (met 1 cijfer achter de komma)
- <math>\tfrac {1}{100} = \tfrac {1}{10^2} = 0{,}01</math> (met 2 cijfers achter de komma)
- <math>\tfrac {2}{100} = 0{,}02</math>
- <math>0{,}0123 = \tfrac {123}{10^4}= \tfrac {123}{10000}</math>
- <math>3{,}14159 = 3 \tfrac {14159}{100000}</math>
Schrijfwijze
Het hoofdtelwoord geeft de teller van een breuk weer, het rangtelwoord de noemer.
- 1 5 een vijfde, 7 10 zeven tiende, 1 2 6 een twee zesde.
- 11 1 5 elf en een vijfde, elf een vijfde, of elf gehelen en een vijfde.
Enkele breuken hebben een eigen naam:
Een derde lijkt een eigen naam te hebben. Het is als breuk een "gewone" combinatie (derde is het rangtelwoord van drie):
- 1 3 een derde (dus niet eenderde)
- 2 3 twee derde.
sina cosa
- 30-10 5
60 24/60
sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = 0 = 0,5345 24
sin a = sin 32 + 18 + 44 60/60 = sin 32,3122
Het eerste voorbeeld is ook als volgt toe te lichten: als men twee taarten elk in vier even grote stukken snijdt, resulteert dat in acht stukken. Ook het delen van breuken is zo te beschrijven: als men anderhalve (1 1⁄2 = 3⁄2) euro uitgeeft aan artikelen die een halve euro per stuk kosten, krijgt men drie van die artikelen, want 3 2 : 1 2 = 3 2 × 2 1 = 3 × 2 2 × 1 = 3.
Rekenvoorbeeld

Bronvermelding
Bronnen, noten en/of referenties:
Meetkunde ( Lichamen )
In het eerste deel van de Meetkunde – de vlakke meetkunde of planimetrie – wordt nagegaan hoe de lengte, de omtrek en het oppervlak van figuren in het tweedimensionale vlak kunnen worden berekend.
In het tweede en (voorlopig) afsluitende deel van de Meetkunde gaat het om het berekenen van het Oppervlak en de Inhoud van lichamen in de driedimensionale ruimte.
Het oppervlak A en de inhoud V van eenvoudige lichamen - zoals de Kubus of het Rechte Parallellepipedum - zijn zonder veel moeite te berekenen met de lengte de breedte en de hoogte van het lichaam. Bij de meer gecompliceerde lichamen - zoals de Kegel, de Piramide of het Prisma – is het berekenen van het oppervlak en de inhoud wat lastiger. De nog gecompliceerdere lichamen zoals als de Holle cilinder , de Afgeknotte kegel en de Afgeknotte piramide , geven nog iets ingewikkelder berekeningen.
Onderverdeling van de lichamen
Bij het onderwerp Lichamen wordt de volgende onderverdeling gemaakt:
- Kubus
- Parallellepipedum
- Prisma
- Cilinder en holle cilinder
- Kegel en afgeknotte kegel
- Piramide en afgeknotte piramide
- Bol
Bij de behandeling van de lichamen zal - waar nodig – met rekenvoorbeelden worden gewerkt!
Kubus
Een Kubus is het meest basale, regelmatige lichaam. Alle 6 vlakken zijn vierkanten die even groot zijn. Waar twee vlakken samenkomen, is een ribbe aanwezig. Een kubus bevat 12 ribben.
De berekening van het oppervlak A en de inhoud V van de kubus is vrij eenvoudig, zoals in het gele vlak duidelijk wordt.


Parallellepipedum
Een Parallellepipedum – ook wel Parallellopipedum of Balk genaamd – heeft net als de kubus 6 vlakken en 12 ribben. De vlakken bij een recht parallellepipedum zijn rechthoeken.
De berekening van het oppervlak en de inhoud van dit lichaam is – net als bij de kubus - vrij eenvoudig, zoals blijkt uit de formules in het gele vlak.


Prisma
Een recht Prisma is een lichaam, dat begrensd wordt door enige vlakken die elkaar volgens evenwijdige lijnen snijden. Verder wordt dit lichaam begrensd door twee evenwijdige vlakken waarin de verbindende ribben en zijvlakken loodrecht op de grondvlakken staan. Hierdoor zijn de verbindende zijvlakken rechthoekig.


Rekenvoorbeeld
Van een recht prisma – als gegeven in de figuur - met een grondvlak in de vorm van een regelmatige vijfhoek met zijden a = 15 cm en een hoogte h = 20 cm, worden het oppervlak A en de inhoud V in het gele kader berekend.
- In Meetkunde ( Veelhoeken ), wordt voor de regelmatige vijfhoek het oppervlak A = 1,721• a2 aangehouden.

Scheef prisma

Als de verbindende ribben en zijvlakken niet loodrecht op het grondvlak staan, dan spreken we van een Scheef Prisma. De berekening van het oppervlak 'A' en de inhoud V is gelijk aan die van een recht prisma.
- Het berekenen van het oppervlak en de inhoud van een scheef prisma zijn al betrekkelijk ingewikkeld, maar zijn toch goed uit te voeren.
Als het bovenvlak van een prisma niet evenwijdig loopt met het grondvlak, dan spreekt men van een Afgeknot Prisma. De berekening van het oppervlak A en de inhoud V is iets gecompliceerder dan van een recht prisma of een scheef prisma.
In de afbeelding is een afgeknot driezijdig prisma weergegeven, en in het gele vlak zijn de bijbehorende formules weergegeven.

Cilinder
Een Cilinder bestaat uit een gebogen oppervlak of cilindermantel, een grondvlak en een bovenvlak. Het bovenvlak is gelijk aan het grondvlak.
Bij de berekening van het oppervlak A en de inhoud V, komt het getal π aan de orde.
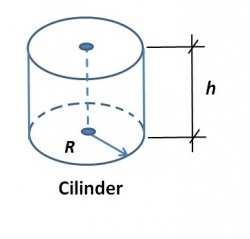

Rekenvoorbeeld
Gegeven een cilinder, als afgebeeld in de figuur. De straal R van de cilinder = 7 cm en de hoogte h bedraagt 18 cm. Het oppervlak A en de inhoud V volgen uit:

Holle cilinder
Een Holle Cilinder – ook wel buis genaamd - bestaat uit een cilinder met een straal R waaruit - als het ware - een cilinder met een straal r is wegenomen. Bij het berekenen van het oppervlak A en de inhoud V zullen om die reden de formules die bij de cilinder horen, moeten worden uitgebreid.
Het grondvlak van de ‘weggenomen’ cilinder wordt met Aw aangeduid. Het manteloppervlak Amw van de weggenomen cilinder is hetzelfde als het manteloppervlak van het achtergebleven cilindrische gedeelte.
Voor de inhoud V geldt, dat van de basiscilinder met straal R en een inhoud Vb een cilinder wordt weggenomen met een straal r en een inhoud Vw.


Rekenvoorbeeld
Een holle cilinder heeft een hoogte h = 10 cm en een straal R van 8 cm. De straal r van de binnencirkel = 4 cm.
Het oppervlak A en de inhoud V zijn met deze gegevens vast te stellen.

Kegel
Een Kegel is een ruimtelijke figuur, en bestaat uit een plat vlak en een gekromd vlak. Het platte vlak is de bodem in de vorm van een cirkel. Het gekromde vlak is de mantel van de kegel.


Afgeknotte kegel
Wordt van een kegel een gedeelte afgesneden - waarbij het snijvlak evenwijdig met het grondvlak loopt - dan vormt het overgebleven lichaam een Afgeknotte Kegel. Het oppervlak A kan worden berekend, door het manteloppervlak van het afgesneden gedeelte van het totale oppervlak af te trekken, en er het oppervlak van het snijvlak aan toe te voegen. Het volume V wordt berekend, door van de oorspronkelijke kegel het volume Va van de afgesneden kegel af te trekken.
Het oppervlak A kan ook rechtstreeks worden berekend, door grondvlak Ag + bovenvlak Ab + het manteloppervlak Am te berekenen.
De formules voor het oppervlak A en de inhoud V - via deze rechtstreekse benadering - zijn in het gele kader opgenomen.


Rekenvoorbeeld
Gegeven een afgeknotte kegel volgens de gegeven afbeelding. Het bovenvlak Ab heeft een straal r = 12 cm, het grondvlak Ag heeft een straal R = 20 cm. De hoogte h bedraagt 15 cm. Het oppervlak A en de inhoud V van de afgeknotte kegel worden in het gele kader berekend.

Piramide
Een Piramide is een ruimtelijk figuur, bestaande uit een grondvlak en een top. Het grondvlak van een piramide kan willekeurig zijn, of gevormd worden door een regelmatige veelhoek. Het oppervlak van een piramide wordt gevormd door het grondvlak Ag + het zijdelings oppervlak Az


Rekenvoorbeeld
Gegeven een regelmatige vierzijdige piramide, als afgebeeld in de figuur.
Het grondvlak van de piramide is een vierkant, waarvan zijde b = a = 20 cm, h = 24 cm. De zijden van de piramiden zijn dus gelijkbenige driehoeken.
De 4 zijden bezitten een oppervlak Ag dat in het gele kader is berekend. Ook de inhoud V wordt berekend.


Afgeknotte piramide

Net als bij een kegel kan van een piramide een gedeelte worden afgesneden. Als hierbij het snijvlak evenwijdig met het grondvlak loopt - dan vormt het overgebleven lichaam een Afgeknotte Piramide.
Het oppervlak A kan worden berekend, door het manteloppervlak van het afgesneden gedeelte van het totale oppervlak af te trekken, en er het oppervlak van het snijvlak aan toe te voegen. Het volume V wordt berekend, door van de oorspronkelijke piramide het volume van de afgesneden piramide af te trekken.
Het oppervlak A kan ook rechtstreeks worden berekend, door grondvlak Ag + bovenvlak Ab + het manteloppervlak Am te berekenen.
De formules voor het oppervlak A via de eerste werkwijze en de inhoud V zijn in het gele kader opgenomen.

Rekenvoorbeeld

Gegeven een afgeknotte vierzijdige piramide, als afgebeeld in de figuur. Het grondvlak van de afgeknotte piramide is een vierkant, waarvan zijde b = a = 30 cm, het bovenvlak heeft zijden d van 22 cm. De hoogte h = 10 cm. De 4 zijden bezitten een oppervlak A dat in het gele kader wordt berekend. Ook de inhoud V wordt berekend.

Bol

Een Bol is een driedimensionaal lichaam waarvan alle punten die het oppervlak vormen, zich op gelijke afstand van het middelpunt bevinden.
Deze gelijke afstand wordt aangegeven als de straal R.

Rekenvoorbeeld
De straal R van een bol = 15 cm.
Het oppervlak A en de inhoud V van de bol volgen uit:

Steradialen

In de verlichtingstechniek wordt - uitgaande van een bolvormige verspreiding van het licht - veelal met radialen gewerkt. In dit geval - waar het een ruimtelijk object betreft - geldt als SI-eenheid van ruimtehoek (ω) de Steradiaal met het symbool sr.
Op het oppervlak van een bol - met een straal R kan een willekeurig vlak - bijvoorbeeld een vierkant - met zijden R worden geprojecteerd. Als vanuit het middelpunt van de bol de straal R van de bol de omtrek van het vierkante vlak uitsnijdt, dan beschrijft deze straal een piramide, die een ruimtehoek ω van een steradiaal omvat.
Aangezien het oppervlak van een bol = 4πR2, is de
totale ruimtehoek ω van een bol dus 4π steradialen.
Rekenvoorbeeld
- De ruimtehoek ω van een halve bol berekenen
- De ruimtehoek ω van de hoekpunten in een kubus berekenen
- In het gele vlak is de berekening hiervan uitgevoerd.

Nawoord
Met het onderdeel Lichamen wordt de Wiskunde hier voorlopig afgesloten. Dat wil niet zeggen, dat er verder geen onderwerpen zijn die in de wiskunde thuishoren. Lichamen bijvoorbeeld kunnen nog verder worden aangevuld met Platonische en Archimedische lichamen.
Platonische lichamen
Platonische lichamen zijn lichamen die passen in een bol, en bevatten slechts één type veelhoek. De kubus en de piramide met een driehoekige basis zijn Platonische lichamen.
Een heel bekend Platonisch lichaam is bijvoorbeeld de Dodecaëder, die 12 (= Dodeca, Grieks) regelmatige vijfhoeken als vlakken bezit.
( Bij de graficus M.C.Escher is zo’n Dodecaëder op een prent van hem aanwezig. http://www.mcescher.nl/galerij/terug-in-nederland/reptielen/ )
Archimedische lichamen
Archimedische lichamen bestaan uit combinaties van regelmatige vlakken als driehoeken, vierkanten vijfhoeken, zeshoeken en achthoeken.
Een zeer bekend Archimedisch lichaam is de afgeknotte icosaëder, die uit 32 vlakken bestaat. De grondvorm – de icosaëder - bestaat uit 20 (= Eíkosi = Grieks) vlakken. Bij de afgeknotte icosaëder, zijn er 20 vlakken zeshoekig en zijn er 12 vijfhoekig.
De vlakverdeling van een voetbal is geheel gebaseerd op de opbouw van een icosaëder.
Verdere onderwerpen
De wiskunde kent verder nog onderwerpen, als:
- Analytische meetkunde
- Vergelijkingen en reeksen
- Functies
- Complexe rekenwijze
- Differentiaal – en integraalrekening
- Fourieranalyse en transformaties
- Lineaire algebra en matrixrekening
- Vectoralgebra en – analyse
- Numerieke wiskunde
Statistiek
Er is nog een belangrijk onderwerp, dat alleen met wiskunde kan worden begrepen, namelijk de Statistiek.
Statistiek is de wetenschap, de methodiek en de techniek van het verzamelen, bewerken, interpreteren en presenteren van gegevens. Het vormt een belangrijk onderdeel van de wiskunde. In de statistiek gaat het dikwijls om de kans dat iets ooit, meermalen of juist nooit gebeurt. Dit wordt ook wel Kansrekening of Waarschijnlijkheidsrekening genoemd.
De statistiek omvat een groot wiskundig gebied, namelijk:
- Combinatieleer
- Waarschijnlijkheidrekening
- Stochastische variabelen en kansverdeling
- Steekproeven en schattingen
- Regressie en correlatie
- Waarnemingsrekening
Bronvermelding
Bronnen, noten en/of referenties:
| a-b
a+b |
0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
|---|---|---|---|---|---|---|---|---|---|---|
| λ | 1,003 | 1,010 | 1,023 | 1,040 | 1,064 | 1,092 | 1,127 | 1,168 | 1,216 | 1,273 |
Radialen
Er is nog een manier om de diverse grootheden van een cirkel te berekenen, namelijk in radialen. In Rondom de cirkel wordt dit thema verder behandeld.
 |
ΔT = ΔT max ( 1 -e -t/τ )
- √3
|
√2,√3,10 log 5,π |
fff
=
Zoltan Kodaly: Zomeravond.
Als vervolgens diagonaal d2 vanuit de linkeronderhoek wordt omgecirkeld, dan is dus ook de onderste zwarte- + de oranje- + de groene lijn samen gelijk aan:
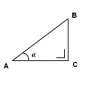
Als van een cirkel de straal r aan de buitenzijde wordt afgewikkeld, dan zal de middelpuntshoek ω een vaste waarde omvatten. De hoek ω wordt uitgedrukt in radialen.
Een radiaal is dus de hoek ω die gevormd wordt door de boog A-B van de cirkel waarbij die boog precies even lang is als de straal r van diezelfde cirkel.
De radiaal wordt ook aldus beschreven:
De radiaal ( rad ) is de vlakke hoek tussen twee stralen r van een cirkel die op de omtrek een boog afsnijden, waarvan de lengte gelijk is aan de straal r.
Een hoek in radialen is dus de verhouding van booglengte en straal.
Dit maakt de radiaal tot een een dimensieloos getal, wat zeer handig is in formules, die hierdoor een eenvoudiger gedaante hebben.
Als de boog A-B = r, en de omtrek van een cirkel is:
A = 2 π r
dan bevat dus de hele cirkel 2 π radialen, wat overeen komt met 360 graden. Omgekeerd == Bronvermelding ==
Bronnen, noten en/of referenties:
geldt ook, dat:
1t0PeWRD
1t0PeWRD
<
Italiano: Scaramuccia
Deutsch: Scaramuz
Datum 1860(1860)
Quelle SAND Maurice. Masques et bouffons (Comedie Italienne). Paris, Michel Levy Freres, 1860
Urheber Maurice Sand
- 2 2/ 9 + 5/ 9 = 2 7/ 9
12 3 • 3 : 9 - √ 36 + 5 - 3 =
128 4/ 7 0 achtenveertig achtenveertig
- P = U • I • cos φ
- P = 3U f • I f • cos φ
waarbij:
- U f = U fase en I f = I fase
- P = 3 U fase• I fase • cos φ
- Moon River, Goodnight Moon, Moon Cloud, Dark of the Moon
haiku (senryu, tanka, waka) en poëzie (met name haikus) waarin wordt gestreefd op impressionistische wijze de ware essentie te vangen.
Over de eindigheid van driehoeken
Inleiding
- Δ BCD ~ Δ ABC

Franciscus 7 feb 2015 12:31 (CET)

