Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Meetkunde ( De cirkel )
Meetkunde ( De cirkel )
- In Rondom de cirkel ( 1 ) wordt ingegaan op de herkomst van het getal π = 3,14159……, dat zo’n bijzondere rol speelt bij de berekening van de omtrek en het oppervlak van een cirkel. Het bijzondere van een cirkel is namelijk, dat er bij berekeningen een bijzonder getal aan te pas moet komen, namelijk de wiskundige constante π. Deze constante - een getal zonder einde - intrigeert al duizenden jaren menig wiskundige.
- Een cirkel kan in principe oneindig groot of oneindig klein zijn, maar zal in de praktijk meestal op gangbare maten uitkomen.
- Een hele cirkel bevat een hoek van 360 0.
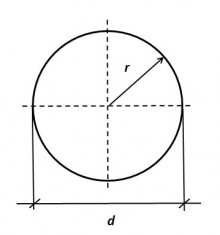
- De omtrek O en het oppervlak A kunnen met de straal r of met de diameter d worden berekend, zoals in het gele kader is aangegeven.
- Er is nog een manier om de diverse grootheden van een cirkel te berekenen, namelijk in radialen. In Rondom de cirkel ( 1 ) wordt dit thema verder behandeld.
Rekenvoorbeeld


Hoeken in een cirkel
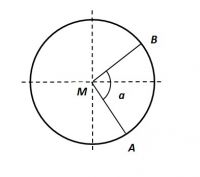
Middelpuntshoek
Een hoek waarvan het hoekpunt samenvalt met het middelpunt M van een cirkel, wordt middelpuntshoek genoemd.

Omtrekshoek
Een hoek waarvan het hoekpunt C op de omtrek van een cirkel ligt, wordt omtrekshoek genoemd.

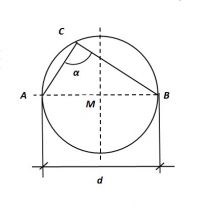

Een bijzondere omtrekshoek is een omtrekshoek met een basis AB = 2r = d.
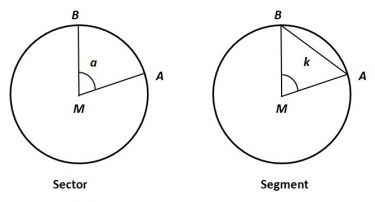
Sector en segment
Het deel van het cirkeloppervlak, ingesloten door een de cirkelboog AB en twee stralen, wordt sector genoemd. Het deel van het cirkeloppervlak, ingesloten door de koorde k en de cirkelboog AB, wordt segment genoemd.

Rekenvoorbeeld

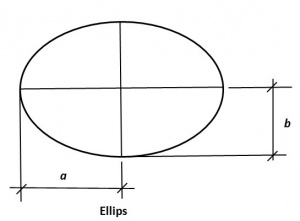
De ellips
De ellips is een bijzondere figuur, aangezien er wél een formule is voor het oppervlak A, maar voor de omtrek O bestaat er geen eensluidende formule.
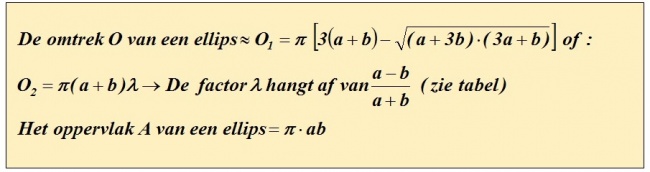

Rekenvoorbeeld

Bronvermelding
Bronnen, noten en/of referenties:
