Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Meetkunde ( Driehoeken )
Meetkunde ( Driehoeken )
Driehoeken (Δ) zijn fundamentele figuren in de meetkunde. Zoals onder meer bij de veelhoeken zal blijken, zijn veel meetkundige figuren opgebouwd uit Δ Δ.
In het vak Goniometrie zijn al enkele eigenschappen van de Δ behandeld, onder meer, dat de som van de hoeken van een Δ = 180 0 .
Soorten driehoeken
Er kunnen diverse driehoeken worden onderscheiden, namelijk:
- De scherphoekige Δ → Bij een scherphoekige Δ zijn alle zijden anders van lengte en zijn alle hoeken verschillend, maar < 90 0 .
- De rechthoekige Δ → Bij een rechthoekige Δ is één hoek altijd 90 0 en zijn de andere hoeken < 90 0 . De zijden kunnen verschillend van lengte zijn.
- De stomphoekige Δ → Bij een stomphoekige Δ is één hoek altijd 90 0 en zijn de andere hoeken < 90 0 en zal één zijde altijd groter zijn dan de andere zijden.
- De gelijkbenige Δ → Bij een gelijkbenige Δ – als bijzondere scherphoekige Δ – zijn twee zijden gelijk aan elkaar en zijn ook de aanliggende hoeken gelijk aan elkaar.
- De gelijkzijdige Δ → Bij een gelijkzijdige Δ – als bijzondere scherphoekige Δ – zijn alle zijden even groot en zijn alle hoeken 60 0.

Omtrek en oppervlak van de Δ
Voor elke Δ geldt, dat:

Voor een gelijkzijdige Δ geldt:

Rekenvoorbeeld
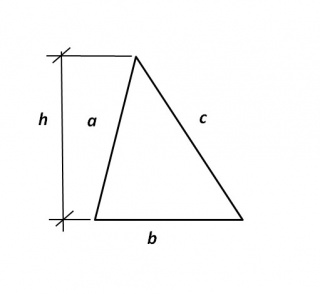
In de gegeven Δ is zijde a = 6 cm , b = 5 cm en c = 7 cm. De hoogte h = 6,5 cm.
De omtrek O en het oppervlak A van de Δ zijn in het gele kader uitgewerkt.
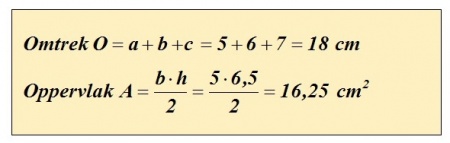
Rekenvoorbeeld als variant op de voorgaande berekening
Gevraagd wordt de omtrek O en het oppervlak A van de Δ, als de gegeven Δ een gelijkzijdige Δ is met zijden a = b = 6 = 6 cm.
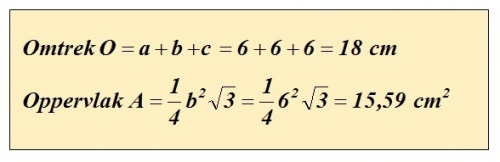
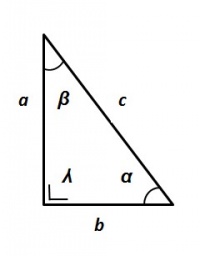
Hoeken van de Δ
Rekenvoorbeeld

Zijden van de rechthoekige Δ
In Algebra ( Machtsverheffen en Worteltrekken ) wordt de stelling van Pythagoras behandeld. Deze luidt:
In een rechthoekige driehoek is de som van de kwadraten van de rechthoekszijden gelijk aan het kwadraat van de schuine zijde.
De stelling kan met de rechthoekige driehoek en de bijbehorende rechthoekszijden
b en c in de vorm van een formule worden uitgedrukt, namelijk:

Rekenvoorbeeld

Bronvermelding
Bronnen, noten en/of referenties:
