Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Rondom de cirkel ( 2 )
In Rondom de cirkel ( 1 ) werd het bijzondere getal π afgeleid door de eigenschappen van een aantal regelmatige veelhoeken te betrekken op de cirkel.
In deze 2e verhandeling over de cirkel wordt eveneens via een aantal regelmatige veelhoeken een bijzondere eigenschap van de cirkel aangetoond.
Het blijkt namelijk, dat tussen het oppervlak en de omtrek van regelmatige veelhoeken een zeker verband aanwezig is. Als dit wordt betrokken op een cirkel, dan blijkt de cirkel de gunstigste verhouding tussen oppervlak en omtrek te bezitten.
Regelmatige veelhoeken
Regelmatige veelhoeken zijn tweedimensionale meetkundige figuren, bestaande uit een eindig aantal lijnstukken die alle dezelfde lengte hebben. Bekende voorbeelden van regelmatige veelhoeken zijn:
- ▪ de gelijkzijdige driehoek
- ▪ het vierkant
- ▪ de regelmatige vijfhoek
- ▪ de regelmatige zeshoek
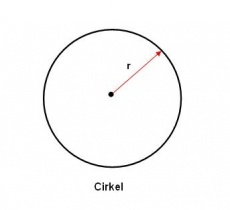
De cirkel - hoewel niet tot de regelmatige veelhoeken gerekend - hoort ook in dit rijtje thuis. De cirkel is in ieder geval ook een tweedimensionale meetkundige figuur met bijzondere eigenschappen, zoals ook al in Rondom de cirkel ( 1 ) is gebleken.
Oppervlakken en omtrekken
De cirkel blijkt van alle meetkundige figuren de figuur te zijn met de grootste
oppervlakte / omtrek- verhouding, of anders gezegd: de cirkel bezit bij een gegeven oppervlak ( A ) van alle meetkundige figuren de kleinste omtrek ( O ). Dit kan met eenvoudige berekeningen worden aangetoond, uitgaande van de formules die bij de oppervlakken en de omtrekken van de regelmatige veelhoeken horen, en die in elk handboek zijn te vinden.
Om het rekenen eenvoudig te houden, wordt uitgegaan van een oppervlak A van 1000 cm 2, waaruit dan weer de omtrek O kan worden afgeleid. In bijgaande tabel zijn de resultaten van deze berekeningen weergegeven.
| Regelmatige veelhoek | Omtrek O (cm) |
|---|---|
| Gelijkzijdige driehoek | 144 |
| Vierkant | 127 |
| Vijfhoek | 121 |
| Zeshoek | 118 |
| Achthoek | 115 |
| Tienhoek | 114 |
| Twaalfhoek | 113 |
| Zeventienhoek | 112,75 |
| Cirkel | 112 |
Verhouding tussen oppervlak en omtrek
Om de verhouding tussen het oppervlak A en de omtrek O in procenten te kunnen uitdrukken, worden de bij de figuren horende formules dimensieloos gemaakt, waarvoor enkele berekeningen nodig zijn. Hierbij wordt uitgegaan van de formules die bij de cirkel horen, waarbij het oppervlak A van een cirkel is:
- Acirkel = π r 2
en de omtrek O van de cirkel is:
- Ocirkel = 2 π r
De dimensie van de straal r is de lengte l, zodat dus r 2 de dimensie l 2 heeft.
Door nu het oppervlak A te delen door de omtrek O in het kwadraat, vallen de dimensies van de lengte l tegen elkaar weg. Verder is er door invoering van de getalwaarden 4π en 100% voor gezorgd, dat de verhouding tussen oppervlak en omtrek bij de cirkel op 100% uitkomt.
Voor alle regelmatige veelhoeken
- uitgezonderd de cirkel - geldt nu:
- 4 π A/O 2 · 100% = < 100%
De resultaten van de berekeningen voor de eerder gekozen regelmatige veelhoeken zijn ondergebracht in bijgaande tabel.
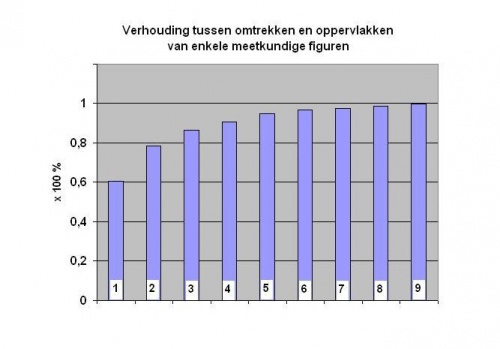
| Regelmatige veelhoek | 4 π A/O 2 · 100% |
|---|---|
| 1. Gelijkzijdige driehoek | 60,5 |
| 2. Vierkant | 78,5 |
| 3. Vijfhoek | 86,5 |
| 4. Zeshoek | 90,7 |
| 5. Achthoek | 94,8 |
| 6. Tienhoek | 96,7 |
| 7. Twaalfhoek | 97,7 |
| 8. Zeventienhoek | 98,8 |
| 9. Cirkel | 100 |
Om nog een beter inzicht te krijgen in de verhouding tussen het oppervlak A en de omtrek O van de berekende veelhoeken, zijn de in de tabel genoemde resultaten weergegeven in bijgaande grafiek.
De nummers in de grafiek komen overeen met de nummers in de tabel.
Samenvatting
Met de wetenschap, dat van alle meetkundige figuren de cirkel bij een gegeven oppevlak A de kleinste omtrek O bezit, is een vergelijking gemaakt met enkele regelmatige veelhoeken. Deze betrekking wordt in dit essay in percentages uitgedrukt, waarbij de cirkel op 100% wordt gesteld.
Zoals te verwachten is, stijgt - naarmate de veelhoek meer vlakken bezit - het percentage, maar zal altijd < 100% zijn.
Links
- In : Rondom de cirkel ( 1 ), nam de cirkel ook een bijzondere plaats in tussen een aantal regelmatige veelhoeken.
- In de oudheid was men al verrukt over de cirkel. Proclus ( 411 - 485 ), een Grieks Neo-Platonisch filosoof en wiskundige, had over de cirkel het volgende te zeggen: De cirkel is de eerste, de eenvoudigste en de meest volmaakte figuur.
- In : Essay: Kunst en Wiskunde I komt ook de cirkel ter sprake.
Zie ook de categorie met mediabestanden in verband met Unit circles op Wikimedia Commons.
Zie ook de categorie met mediabestanden in verband met Circle geometry op Wikimedia Commons.