Gebruiker:Franciscus/kladblok

Deelonderwerp

Deze pagina gebruik ik om nieuwe artikelen even op te bergen en te bewerken, vóórdat ik ze als bijdrage op Wikisage zet. Ook kan ik hier enkele geheugensteuntjes kwijt.
Franciscus 4 feb 2009 14:55 (UTC)

Das Glasperlenspiel

Das Glasperlenspiel (nl) ( Het kralenspel ) is een roman uit 1943 van de Zwitserse schrijver Herman Hesse. Deze roman vormt binnen zijn oeuvre een hoogtepunt, en kan worden beschouwd als zijn magnum opus. In de roman wordt het gevecht van de mens tegen de machtswellust weergegeven.Het gaat over de strijd van de mens tegen ideologieën.
Hermann Hesse kreeg in 1946, kort na het verschijnen van Het Kralenspel, de Nobelprijs voor literatuur en ook de Goetheprijs. Critici vonden dat niet terecht, omdat hij geen vormvernieuwer zou zijn. Maar zijn vele lezers beslissen daar - ook nu nog - anders over.

Inhoud

Het Kralenspel behoort tot die veelomvattende epische werken, die de problematiek van de Europese beschaving samenvatten. Dit wordt door de schrijver Hermann Hesse tot uitdrukking gebracht in een fictieve biografie van de hoofdpersoon Josef Knecht, die we volgen in zijn opleiding, carrière en intellectuele ontwikkeling in de denkbeeldige staat Kastalië.
Jozef Knecht ( nomen est omen ), die uit een eenvoudige familie stamt, - maar zeer begaafd is - brengt het in deze elite-orde tot een van de hoogste posten, namelijk tot Magister Ludi( Spelmeester ).

De officiële titel van het werk luidt als volgt:

HET KRALENSPEL Poging tot een levensbeschrijving van Magister Ludi Josef Knecht,gevolgd door Knechts nagelaten werken.

Het Kralenspel

Het Kralenspel ²⁾ speelt een belangrijke rol in het leven van de ingezetenen die voornamelijk uit erudiete jonge mannen bestaat.
Waarover het Kralenspel gaat wordt niet precies duidelijk gemaakt. De regels van het spel zijn zó ingewikkeld, dat ze bijna niet zijn uit te leggen. Het spelen vergt dan ook jaren van gedisciplineerde studie van muziek, wiskunde en cultuurgeschiedenis. Het is eigenlijk te beschouwen als een synthese van alle kunsten en studies.
In de inleiding van de roman wordt wel een beschouwing gegeven over de regels, de tekentaal en de grammatica van het Spel. Uitgelegd wordt ook, dat deze geheimtaal in staat is de inhouden en uitkomsten van nagenoeg alle wetenschappen en hun onderlinge relaties tot uitdrukking te brengen. Belangrijk bij het spel is, dat de spelers verbanden vinden tussen onderwerpen die op het eerste gezicht niets met elkaar te maken lijken te hebben. Het spel lijkt enigszins op het Japanse spel Go, maar dan zonder pionnen of symbolen.

Eschholz

In de elitescholen van Katalië wordt het contact met de buitenwereld zoveel mogelijk buitengesloten, in het bijzonder politieke kwesties. Deze tegenstrijdigheden zijn het die cruciaal zijn voor het leven van de held, Josef Knecht.
Als jongen wordt hij door de plaatselijke Latijnse school met behulp van de Muziekmeester - één van de hoge oversten - als flos juventutis - ook wel electi¹⁾ genoemd - toegewezen en geplaatst op een eliteschool in de staat Kastalia. Het wordt de school van Eschholz: het grootste en het modernste scholencomplex van Kastalië. De school omsluit een rechthoekig plein met vijf bomen in de vorm van een dobbelsteen. Het gebouw zelf wordt gedragen door vijf zuilen.
Het getal 5 is hierbij niet geheel toevallig: het symboliseert namelijk: zich een doel stellen, geduld en trouw ontwikkelen.
In Eschholz verandert Josef Knecht wezenlijk door de goede verstandhouding met de muziekmeester, die hem ook aanzet tot meditatie, waardoor hij zich volledig schikt in de regels van de Orde.
Meer en meer maakt hij zich de vaardigheden eigen die behoren bij de diepgaande kennis van de wetenschap en de muziek.
Na enkele jaren van studie in Eschholz wordt hij met enkele medestudenten overgeplaatst naar de Pedagogische Provincie Waldzell; het hoogste niveau in de Orde.

Waldzell

In Waldzell ontwikkelt Josef Knecht zich verder, maar komt af en toe ook in moeilijkheden met zijn omgeving. Dit draagt bij aan de vorming van zijn karakter, waardoor de schuchtere en wat verlegen jongen vrijer in de omgang wordt.
Als hij tenslotte klaar is met zijn studie, breekt voor hem - als 24-jarige - een periode van vrijheid aan, waarin hij ongehinderd verdere studies kan gaan maken van diverse wetenschappen, muziek, poëzie of andere richtingen.
Intussen legt hij zich ook toe op het Kralenspel, dat hij met een kameraad samen probeert te doorgronden. OP een gegeven moment meent hij dat hij de zin van het Spel dicht is genaderd, en meent dat hij dit niet tot zijn beroep moet maken. Het zal echter allemaal anders lopen.

De Oudere Broeder

Josef Knecht komt bij zijn vrije studies terecht bij de Chinese taal en gaat zich interesseren voor het orakelspel I Tjing, ook wel het Boek der Veranderingen genoemd.
Hij komt erachter, dat in een bamboebos een man woont die had gestudeerd en die de Oudere Broeder wordt genoemd.
Hij gaat naar het bamboebos en treft daar de man aan, en spreekt enkele Chinese begroetingswoorden tot hem:

• De jonge leerling verstout zich zijn opwachting te maken bij de Oudere Broeder.

De welopgevoede gast is welkom , zei de Oudere Broeder.
Knecht blijft en helpt brandhout te sprokkelen, penselen schoon te spoelen en de Chinese kalender bij te houden.
Elke keer als hij het gesprek op andere onderwerpen wil brengen, krijgt hij een koan³⁾ als antwoord:

• Zware wolken, geen regen.

Intussen bestudeert hij de I Tsjing en leert hij om te gaan met het orakelspel met de bamboestokjes en de bijbehorende vierenzestig hexagrammen. Op een dag legt de Oudere broeder het stokjesorakel voor Josef Knecht, waaruit een berekening volgt die naar het hexagram Meng ( Jeugddwaasheid ) verwijst en waarvan de uitslag luidt:

Jeugdzotternij heeft welslagen.

Niet ik zoek de jonge dwaas.

De jonge dwaas zoekt mij.

Bij het eerst orakel geef ik antwoord.

Twee, driemaal vragen is lastig vallen.

Wie mij lastig valt geef ik geen antwoord.

Bevorderlijk is standvastigheid.

Deze vermaning en aansporing blijft hij, ook in zijn verdere leven steeds overdenken.
Na maanden keert hij weer terug naar Waldzell, en krijgt steeds meer inzicht in Het Kralenspel. Hij blijft zich afvragen, of het Spel werkelijk het allerhoogste is van Kastalië. Lang hoeft hij hier niet over na te denken, want al spoedig wordt hem gevraagd een verzoek tot opname in de Orde in te dienen. Gelijk krijgt hij opdracht in een klooster te Mariafels als leraar te gaan fungeren en belangstellenden in te leiden in het Kralenspel.

Mariafels

In de eerste weken vraagt Knecht zich af, wat hij eigenlijk in Mariafels doet en beseft, dat zijn verblijf daar ook tot doel had zijn eigen inzicht te vergroten.
Al spoedig vraagt de abt of hij hem de beginselen van de I Tsjing wil bijbrengen en leert hij een invloedrijke historicus kennen met wie hij vele gesprekken heeft. Na twee jaar verblijf daar wordt hij teruggeroepen voor een 'korte' vakantie. In Waldzell krijgt hij de opdracht terug te keren naar Mariafels, met als geheime missie zich nog meer met de historicus bezig te houden en hem langzaam zien te winnen voor een overeenkomst tussen het Vaticaan en Katalië. Op een gegeven moment heeft de geleerde door wat de bedoelingen zijn van Josef Knecht, maar dat staat hun goede verhouding niet in de weg.
De goede samenwerking tussen deze twee mannen, leidt tenslotte tot een akkoord tussen Rome en Kastalië.

Magister Ludi

De terugkeer van Jozef Knecht naar Waldzell wordt overschaduwd door de dood van Magister Ludi Thomas, die tijdens het jaarlijkse Ludus Solemnis ( Feestelijk Spel ) overlijdt. Uit een aantal kandidaten wordt Josef Knecht met meerderheid van stemmen gekozen tot Magister Ludi en ontvangt hij het daarbij behorende ornaat en de sleutels. De Muziekmeester, die hem al die jaren met raad en daad heeft bijgestaan, geeft hem ook nu - bij de aanvaarding van het hoge ambt - weer allerlei raadgevingen mee.
Het lukte Knecht in zijn proeftijd de weerstand tegen hem te doorbreken en het volledige vertrouwen van de repetitoren te verwerven.
Samen met zijn studievriend en tegenpool Fritz Tegularius, ontwerpt hij een voor het jaarlijks Ludus Solemnis prachtig Spel van het Chinese huis, dat zeer succesvol is en waar nog lang daarna over gepraat en geschreven wordt.

Bezinning

Intussen blijkt de oude muziekmeester zich terug te trekken en langzaam afscheid van het leven te nemen. Jozef Knecht maakt nu een moeilijke tijd door en overweegt het volgende: Men denkt er niet graag aan, dat Kastalië en het Kralenspel eens weer moeten vergaan, en toch moet men eraan denken. Ondertussen slaan langzaam nog meer twijfels toe, die uiteindelijk leidden tot zijn afscheid van ambt en Provincie. In gedachten was hij zich reeds aan het bezighouden met weggaan uit Kastalië. Intussen heeft hij een lang gesprek met zijn studievriend Plinio Designori, die Kastalië destijds moest verlaten. De ontstane breuk wordt hierna weer hersteld. Zijn vriend geeft Knecht ook wat meer inzicht in het leven buiten de muren, waardoor hij zich op die manier beter los kon maken van Kastalië, en waardoor de wens om uit treden langzamerhand werd omgezet in een besluit. Na enige tijd bezoekt Knecht zijn vriend in de hoofdstad en maakt kennis met zijn vrouw en hun nogal eigengereid zoontje Tito, wiens opvoeding het echtpaar zorgen baart.

Ontslagaanvraag

Langzaam neemt het komende afscheid concrete vormen aan. Jozef Knecht wil natuurlijk als hij eenmaal buiten de muren zal zijn, zich daar verdienstelijk gaan maken. Het liefst wil hij zich als privéleraar gaan vestigen. Op een gegeven moment besluit hij de knoop door te hakken en schrijft hij aan de Dienst een verzoek, genaamd:

• Het schrijven van de Magister Ludi aan de Pedagogische Dienst

In een breedvoerig opgestelde verzoek tot ontheffing uit zijn ambt, gaat hij uitvoerig in op de overwegingen die hem tot deze stap hebben aangezet. Hij gaat eerst in op de rijke geschiedenis van Kastalië en gaat vervolgens over tot kritische opmerkingen omtrent de arrogantie van de Orde en het standsbewustzijn dat men meent te moeten bezitten. Ook maakt hij opmerkingen over het gebrek aan inzicht in het geheel der volkeren, in de wereld en de wereldgeschiedenis.
Hij merkt op, dat de buiten de muren werkzame docenten de enigen zijn die werkelijk aan het doel van Kastalië beantwoorden en iets terugdoen voor het vele dat ons wordt geschonken.
Als reden van zijn verzoek, geeft Knecht onder meer aan, dat hij al tekenen waarneemt, dat in de nabije toekomst Het Kralenspel als eerste verloren zal gaan. Hij betreurt dit, maar acht het niet zijn taak het einde van het Spel te verhinderen of uit te stellen. Als afsluiting verzoekt hij de Dienst hem van zijn ambt als Magister Ludi te ontheffen.

Zoals te verwachten viel, wordt het verzoek van Jozef Knecht afgewezen. Wel is men zeer ingenomen met het hartverwarmend en spiritueel rondschrijven. Zij menen echter ook, dat de brief in kwestie een niet geslaagde poging tot vernieuwing is, die zij moeten afwijzen. Als slot van het betoog, geven zij de Magister opdracht het eervolle ambt te blijven bekleden. Wel is er enige ongerustheid over de in Knecht's brief genoemde vermindering of bedreiging van zijn geschiktheid voor het hoge ambt.

Bronvermelding

Bronnen, noten en/of referenties:

• ¹⁾ (Latijn) Flos juventutis = Bloem van de jeugd, Electi = Uitverkorene.
• ²⁾ De vertaling uit het Duits van Das Glasperlenspiel naar de titel: Het Kralenspel, kan helaas aanleiding geven tot een wat verwarrende sfeer, alsof het om een kinderspelletje zou gaan.
• De Franse en Engelse vertaling van de titel komen wat dichter in de buurt van de oorspronkelijke bedoeling, namelijk: Le Jeux des perles verre en The glass bead game.
• In de vertaling naar het Frans van Das Glasperlenspiel, wordt - wat niet gebruikelijk is - de naam Josef Knecht omgezet in Joseph Valet ( Valet = dienaar, knecht ), hoewel in zijn omgeving ook enkele keren toespelingen op de naam Knecht worden gemaakt .
• ³⁾ Koans zijn zenraadsels zonder absolute antwoorden. Het is een uitspraak of onoplosbaar raadsel dat in het zenboeddhisme tot doel heeft de student te verwarren, door het denken met een zodanige paradox te confronteren, dat het op de achtergrond treedt ten opzichte van de directe waarneming. Het gaat bij een koan dus niet zozeer om het oplossen van het raadsel, maar meer om het inzicht.

Das Glasperlenspiel (nl) ( Het kralenspel ) is een novelle uit 1943 van de Zwitserse schrijver Herman Hesse. Deze novelle vormt binnen zijn oeuvre een hoogtepunt, en kan worden beschouwd als zijn magnum opus.

Das Glasperlenspiel

Das Glasperlenspiel (nl) (Het kralenspel) is een roman uit 1943 van de Zwitserse schrijver Herman Hesse. Deze roman vormt binnen zijn oeuvre een hoogtepunt, en kan worden beschouwd als zijn magnum opus, waarin het gevecht van de mens tegen de machtswellust wordt weergegeven en wordt afgerekend met dictaturen. Het gaat over de strijd van de mens tegen ideologieën.

Inhoud

Het Kralenspel behoort tot die veelomvattende epische werken, die de problematiek van de Europese beschaving samenvatten. Dit wordt door de schrijver Hermann Hesse tot uitdrukking gebracht in een fictieve biografie van de hoofdpersoon Josef Knecht, die we volgen in zijn opleiding, carrière en intellectuele ontwikkeling in de de denkbeeldige staat Kastalië.
Jozef Knecht (nomen est omen), die uit een eenvoudige familie stamt, - maar zeer begaafd is en nobel van inborst - brengt het in deze elite-orde tot een van de hoogste posten, tot Magister Ludi. Het Kralenspel speelt een belangrijke rol in het leven van de ingezetenen die uit voornamelijk jonge, erudiete mensen bestaat. Waarover het Kralenspel gaat wordt niet precies duidelijk gemaakt. De regels van het spel zijn zo ingewikkeld, dat ze bijna niet zijn uit te leggen. Het spelen vergt dan ook jaren van gedisciplineerde studie van muziek, wiskunde en cultuurgeschiedenis. Het is eigenlijk te beschouwen als een synthese van alle kunsten en studies.
In de inleiding van het boek wordt hierover wel een beschouwing gegeven over de regels, de tekentaal en de grammatica van het Spel . Gezegd wordt ook, dat deze geheimtaal in staat is de inhouden en uitkomsten van nagenoeg alle wetenschappen en hun onderlinge relaties tot uitdrukking te brengen. Belangrijk bij het spel is, dat de spelers verbanden vinden tussen onderwerpen die op het eerste gezicht niets met elkaar te maken lijken te hebben. Daarnaast wordt het contact met de buitenwereld zoveel mogelijk buitengesloten, in het bijzonder politieke kwasties. Deze tegenstrijdigheden zijn het die cruciaal zijn voor het leven van de held, Josef Knecht zijn. Als jongen wordt hij van de plaatselijke Latijnse school weggehaald en geplaatst op de eliteschool in de staat Kastalia..Wezenlijk verandert hij door de goede verstandhouding met de muziekmeester – een van de hoge oversten – schikt hij zich volledig in de regels van de Orde. Meer en meer,maakt hij zich de vaardigheden eigen die behoren bij de diepgaande kennis van de wetenschap de muziek en de meditatie en ten slotte het Kralenspel. Hierdoor stijgt hij steeds hoger in de hiërarchie, totdat het uiteindelijk een van de hoogste rangen bereikt, namelijk die van Magister Ludi.

Het Kralenspel is een utopische roman die het gevecht van de mens tegen de machtswellust weergeeft en afrekent met dictaturen. Het gaat over de strijd van de mens tegen ideologieën. Het Kralenspel is een utopische roman over een spel, dat alle wetenschap en kunst omvat.
De wereld van een soort monastieke orde speelt zich in de toekomst af in de denkbeeldige staat Kastalië.
Het kralenspel speelt een belangrijke rol in het leven van de ingezetenen die uit voornamelijk jonge mensen bestaat. Waarover het Kralenspel precies gaat wordt nooit geheel duidelijk. De regels van het spel zijn zo ingewikkeld, dat ze bijna niet uit te leggen zijn, laat staan te begrijpen. Het spelen vergt dan ook jaren van gedisciplineerde studie van muziek, wiskunde en cultuurgeschiedenis. Het is eigenlijk te beschouwen als een synthese van alle kunsten en studies. Het spel gaat over verschillende werelden en tijden.
Belangrijk bij het spel is, dat de spelers verbanden vinden tussen onderwerpen die op het eerste gezicht niets met elkaar te maken lijken te hebben.
De hoofdpersoon van deze novelle - Jozef Knecht - voert ons door de

{{Overline| (12)}} om ergens een lijntje boven te trekken

{{Overline|24}}

12
24
12
--
24

Breuken

a ^b⁄_c: a b/c (geheel getal, teller en noemer) ^a⁄_b: a/b (teller en noemer) ¹⁄_a: 1/a (alleen noemer)

12
--
24

{{Overline|24}}

12
24

---

 44 /

sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = sin 32,3122 0 = 0,5345 24

---

<math>\tfrac {1}{10} = \tfrac {1}{10^1} = 0{,}1</math> (met 1 cijfer achter de komma)

<math>\tfrac {1}{100} = \tfrac {1}{10^2} = 0{,}01</math> (met 2 cijfers achter de komma)

<math>\tfrac {2}{100} = 0{,}02</math>

<math>0{,}0123 = \tfrac {123}{10^4}= \tfrac {123}{10000}</math>

<math>3{,}14159 = 3 \tfrac {14159}{100000}</math>

Schrijfwijze

Het hoofdtelwoord geeft de teller van een breuk weer, het rangtelwoord de noemer.

•  1 / 5  een vijfde,  7 /10 zeven tiende, 1  2 /6 een twee zesde.
• 11  1 /5 elf en een vijfde, elf een vijfde, of elf gehelen en een vijfde.

---

Enkele breuken hebben een eigen naam:

•  1 / 2  half
•  1 / 4  kwart
•  3 /4 driekwart
• 1  1 /2 anderhalf

---

Een derde lijkt een eigen naam te hebben. Het is als breuk een "gewone" combinatie (derde is het rangtelwoord van drie):

•  1 / 3  een derde (dus niet eenderde)
•  2 /3 twee derde.

---

 sina /cosa

•  30-10 /5

 60 /24/60

sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = 0 = 0,5345 24

sin a = sin 32 + 18 +  44 /60/60 = sin 32,3122

Het eerste voorbeeld is ook als volgt toe te lichten: als men twee taarten elk in vier even grote stukken snijdt, resulteert dat in acht stukken. Ook het delen van breuken is zo te beschrijven: als men anderhalve (1 ¹⁄₂ = ³⁄₂) euro uitgeeft aan artikelen die een halve euro per stuk kosten, krijgt men drie van die artikelen, want  3 /2 :  1 / 2  =  3 /2 ×  2 /1 =  3 × 2 /2 × 1 = 3.

Rekenvoorbeeld

Bronvermelding

Bronnen, noten en/of referenties:

• Meetkunde ( Inleiding )
• Meetkunde ( Driehoeken )
• Meetkunde ( Veelhoeken )
• Meetkunde ( De cirkel )
• Rondom de cirkel ( 1 )
• Rondom de cirkel ( 2 )

Dit artikel valt onder beheer van Dorp:Luisterrijk.

a-b a+b	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
λ	1,003	1,010	1,023	1,040	1,064	1,092	1,127	1,168	1,216	1,273

Radialen

Er is nog een manier om de diverse grootheden van een cirkel te berekenen, namelijk in radialen. In Rondom de cirkel wordt dit thema verder behandeld.

• SEPTEMBER op YouTube

ΔT = ΔT _max ( 1 -e ^-t/τ )

√3

√2,√3,10 log 5,π

fff

=

Zoltan Kodaly: Zomeravond.

Als vervolgens diagonaal d₂ vanuit de linkeronderhoek wordt omgecirkeld, dan is dus ook de onderste zwarte- + de oranje- + de groene lijn samen gelijk aan:

Als van een cirkel de straal r aan de buitenzijde wordt afgewikkeld, dan zal de middelpuntshoek ω een vaste waarde omvatten. De hoek ω wordt uitgedrukt in radialen.
Een radiaal is dus de hoek ω die gevormd wordt door de boog A-B van de cirkel waarbij die boog precies even lang is als de straal r van diezelfde cirkel. De radiaal wordt ook aldus beschreven:
De radiaal ( rad ) is de vlakke hoek tussen twee stralen r van een cirkel die op de omtrek een boog afsnijden, waarvan de lengte gelijk is aan de straal r. Een hoek in radialen is dus de verhouding van booglengte en straal.
Dit maakt de radiaal tot een een dimensieloos getal, wat zeer handig is in formules, die hierdoor een eenvoudiger gedaante hebben.
Als de boog A-B = r, en de omtrek van een cirkel is:

A = 2 π r

dan bevat dus de hele cirkel 2 π radialen, wat overeen komt met 360 graden. Omgekeerd == Bronvermelding ==

Bronnen, noten en/of referenties:

• Meetkunde ( Inleiding )
• Meetkunde ( Driehoeken )
• Meetkunde ( Veelhoeken )
• Meetkunde ( De cirkel )
• Rondom de cirkel ( 1 )
• Rondom de cirkel ( 2 )

geldt ook, dat:

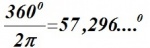
1t0PeWRD 1t0PeWRD

<

• Ungarischer Tanz nr.5 op YouTube

Italiano: Scaramuccia Deutsch: Scaramuz Datum 1860(1860)

Quelle SAND Maurice. Masques et bouffons (Comedie Italienne). Paris, Michel Levy Freres, 1860

Urheber Maurice Sand

2 ²/ ₉ + ⁵/ ₉ = 2 ⁷/ ₉

12 ³ • 3 : 9 - √ 36 + 5 - 3 =

128 ⁴/ ₇ ⁰ achtenveertig achtenveertig

• P = U • I • cos φ
• P = 3U _f • I _f • cos φ

waarbij:

• U _f = U _fase en I _f = I _fase
• P = 3 U _fase• I _fase • cos φ

Moon River, Goodnight Moon, Moon Cloud, Dark of the Moon

haiku (senryu, tanka, waka) en poëzie (met name haikus) waarin wordt gestreefd op impressionistische wijze de ware essentie te vangen.

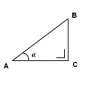
Over de eindigheid van driehoeken

Dit is een gebruikersessay geschreven door Franciscus 30 jan 2015 16:46 (CET)

Inleiding

Δ BCD ~ Δ ABC

Franciscus 7 feb 2015 12:31 (CET)