Wikisage, de vrije encyclopedie van de tweede generatie, is digitaal erfgoed
Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Meetkunde ( Vierhoeken ): verschil tussen versies
Naar navigatie springen
Naar zoeken springen
Geen bewerkingssamenvatting |
Geen bewerkingssamenvatting |
||
| (2 tussenliggende versies door dezelfde gebruiker niet weergegeven) | |||
| Regel 3: | Regel 3: | ||
* '''Het vierkant ''' → Bij een '''vierkant''' zijn ''alle zijden'' even ''groot'' en zijn ''alle'' hoeken '''''90<sup> 0</sup>''''' . | * '''Het vierkant ''' → Bij een '''vierkant''' zijn ''alle zijden'' even ''groot'' en zijn ''alle'' hoeken '''''90<sup> 0</sup>''''' . | ||
* '''De rechthoek ''' → Bij een '''rechthoek''' zijn de ''twee'' verticale zijden ''gelijk'' aan elkaar. Ook de twee ''horizontale'' zijden zijn ''gelijk'' aan elkaar. Alle hoeken zijn '''''90<sup> 0</sup>''''' . | * '''De rechthoek ''' → Bij een '''rechthoek''' zijn de ''twee'' verticale zijden ''gelijk'' aan elkaar. Ook de twee ''horizontale'' zijden zijn ''gelijk'' aan elkaar. Alle hoeken zijn '''''90<sup> 0</sup>''''' . | ||
* '''De ruit''' → Bij een '''ruit''' zijn ''alle'' zijden even groot en zijn ''twee'' hoeken altijd '''''> | * '''De ruit''' → Bij een '''ruit''' zijn ''alle'' zijden even groot en zijn ''twee'' hoeken altijd '''''> 90<sup> 0</sup>''''' . De andere ''twee'' hoeken zijn'' '''< 90<sup> 0</sup>''''' . | ||
* '''Het parallellogram ''' → Bij een '''parallellogram''' zijn de ''twee'' schuine zijden gelijk aan elkaar, even als de ''aanliggende'' hoeken. Ook de twee ''horizontale'' zijden zijn gelijk aan elkaar. Twee hoeken van het parallellogram zijn altijd '''''> 90<sup> 0</sup>''''' . De andere twee hoeken zijn '''''< 90<sup> 0</sup>''''' . | * '''Het parallellogram ''' → Bij een '''parallellogram''' zijn de ''twee'' schuine zijden gelijk aan elkaar, even als de ''aanliggende'' hoeken. Ook de twee ''horizontale'' zijden zijn gelijk aan elkaar. Twee hoeken van het parallellogram zijn altijd '''''> 90<sup> 0</sup>''''' . De andere twee hoeken zijn '''''< 90<sup> 0</sup>''''' . | ||
* '''Het trapezium ''' → Bij een '''trapezium''' ''kunnen'' de twee schuine zijden gelijk of ongelijk aan elkaar zijn. De twee horizontale zijden zijn ''altijd'' anders van lengte. De basishoeken zijn'''' altijd '''''< 90<sup> 0</sup>''''' . De andere twee hoeken zijn '''''> 90<sup> 0</sup>. | * '''Het trapezium ''' → Bij een '''trapezium''' ''kunnen'' de twee schuine zijden gelijk of ongelijk aan elkaar zijn. De twee horizontale zijden zijn ''altijd'' anders van lengte. De basishoeken zijn'''' altijd '''''< 90<sup> 0</sup>''''' . De andere twee hoeken zijn '''''> 90<sup> 0</sup>.''''''' | ||
'''''''* '''De vierhoek''' → Bij een '''vierhoek''''' kunnen alle zijden ''ongelijk'' van lengte zijn en er kunnen maximaal twee hoeken '''''> 90<sup> 0</sup>'' zijn'''. | * '''De vierhoek''' → Bij een '''vierhoek''''' kunnen alle zijden ''ongelijk'' van lengte zijn en er kunnen maximaal twee hoeken '''''> 90<sup> 0</sup>'' zijn'''. | ||
[[Afbeelding: | [[Afbeelding:VK-QQQ.jpg|550px|centre|]] | ||
==Omtrek, oppervlak en hoeken van vierhoeken== | ==Omtrek, oppervlak en hoeken van vierhoeken== | ||
===Vierkant=== | ===Vierkant=== | ||
Huidige versie van 21 jun 2014 om 11:46
Als algemene regel geldt, dat de som van de hoeken van een vierhoek = 360 0.
Er kunnen diverse vierhoeken worden onderscheiden, namelijk:
- Het vierkant → Bij een vierkant zijn alle zijden even groot en zijn alle hoeken 90 0 .
- De rechthoek → Bij een rechthoek zijn de twee verticale zijden gelijk aan elkaar. Ook de twee horizontale zijden zijn gelijk aan elkaar. Alle hoeken zijn 90 0 .
- De ruit → Bij een ruit zijn alle zijden even groot en zijn twee hoeken altijd > 90 0 . De andere twee hoeken zijn < 90 0 .
- Het parallellogram → Bij een parallellogram zijn de twee schuine zijden gelijk aan elkaar, even als de aanliggende hoeken. Ook de twee horizontale zijden zijn gelijk aan elkaar. Twee hoeken van het parallellogram zijn altijd > 90 0 . De andere twee hoeken zijn < 90 0 .
- Het trapezium → Bij een trapezium kunnen de twee schuine zijden gelijk of ongelijk aan elkaar zijn. De twee horizontale zijden zijn altijd anders van lengte. De basishoeken zijn' altijd < 90 0 . De andere twee hoeken zijn > 90 0.''
- De vierhoek → Bij een vierhoek kunnen alle zijden ongelijk van lengte zijn en er kunnen maximaal twee hoeken > 90 0 zijn.
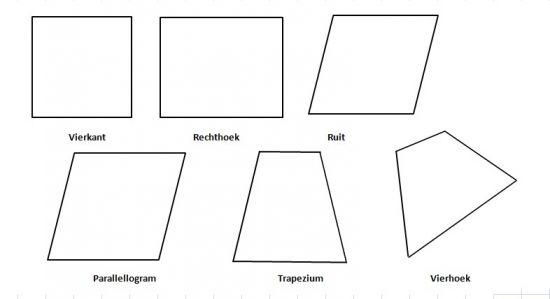
Omtrek, oppervlak en hoeken van vierhoeken
Vierkant
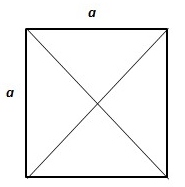
Rekenvoorbeeld
De de omtrek O van een vierkant = 24 cm. De omtrek O en de lengte van een diagonaal in dat vierkant zijn in het gele vlak berekend.
Rechthoek
Ruit
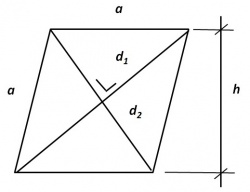
Rekenvoorbeeld
Van een ruit met zijde a = 5 cm, waarvan de scherpe hoeken = 60 0 zijn, wordt gevraagd het oppervlak A te berekenen.
Dit blijkt op drie manieren mogelijk te zijn:
Parallellogram
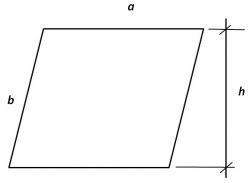
Trapezium
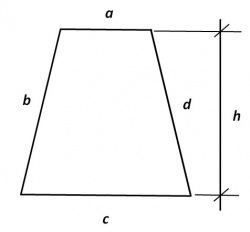
Vierhoek
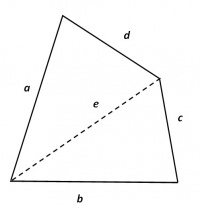
Rekenvoorbeeld
Van de gegeven vierhoek zijn de zijden a en b = 6 cm. De diagonaal e is eveneens 6 cm. Als de zijden d en e = 4 cm zijn, dan is met deze gegevens de omtrek O en het oppervlak A te berekenen.
Bronvermelding
Bronnen, noten en/of referenties: