Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Gebruiker:Franciscus/kladblok
Quadrivium
Quadrivium ( Latijn = viersprong,vier manieren ) was in de Middeleeuwen de tweede leergang van de universitaire opleiding, deel uitmakend van de zeven Artes Liberales, ( de vrije kunsten ), die de muziek, wiskunde, geometrie en astronomie omvatte. Nadat de student het Trivium ( drie manieren of wegen ) met goed gevolg had doorlopen, was hij baccalaureus en was hij in staat het vierjarig Quadrivium te gaan volgen 1).
Het trivium bestond uit de vakken:
- Grammatica
- Retorica
- Dialectiek.
Het quadrivium bestond uit de vakken
- Rekenkunde
- Meetkunde
- Muziek
- Astronomie
Na de voltooiing van deze vakken was de afgestudeerde klaar voor een geestelijke of ambtelijke functie.
Deze in onze ogen wellicht wat vreemde combinatie lag destijds voor de hand: al in de oudheid herleidde men de schoonheid van de muziek en de kosmos tot eenvoudige wiskundige principes.
Opbouw
Het quadrivium is opgebouwd uit de vier zogeheten vrije kunsten van getal, meetkunde, muziek en kosmologie. Dit viertal werd bestudeerd vanaf de oudheid tot de renaissance, in een poging om door te dringen tot de aard van de werkelijkheid.
Het quadrivium is een synthese van getal, ruimte en tijd:
- meetkunde is getal in de ruimte
- muziek is getal in de tijd
- kosmos is de uitdrukking in ruimte en tijd
Getal, muziek en meetkunde weerspiegelen de metafysische waarheid: de eenheid van het goede, het ware en het schone. Het universele onderzoek naar deze thema’s vormde een voorafspiegeling van de natuurwetenschappen.
Boek

Het Quadrivium is in 2010 in boekvorm verschenen bij Wooden books Limited in het Verenigd Koninkrijk. De Nederlandstalige editie verscheen in 2014 bij Librero 1)
Dit is het eerste boek sinds vele eeuwen waarin het klassieke quadrivium weer wordt verenigd, waardoor de basiskennis beschikbaar wordt voor iedereen. Dit meer dan 400 pagina’s tellende boek bundelt voor het eerst in honderden jaren deze verschillende disciplines. De opzet van het boek is simpel: links staat een korte tekst, en rechts een kleine afbeelding in zwart-wit.
Het boek beperkt zich niet tot het Quadrivium van de Middeleeuwen, maar laat ook de ontwikkelingen zien die daarna zijn gekomen.
Indeling
De vier onderwerpen van het quadrivium zijn in het boek Quadrivium ingedeeld in zes onderdelen, namelijk:
- Boek I ----- Heilige getallen
- Boek II ---- Gewijde meetkunde
- Boek III --- Platonische en archimedische lichamen
- Boek IV --- Harmonograaf
- Boek V ---- Muzikale elementen
- Boek VI --- Toeval in het zonnestelsel
In deze onderdelen zijn enkele afgeleide begrippen opgenomen, die in de Middeleeuwen nog niet bekend waren. Ze vormen een uitbreiding van de basisbegrippen en ................. .
Boek I - Heilige getallen
De ondertitel van Heilige getallen luidt:
- De geheime kwaliteiten van kwantiteiten
In het onderdeel Heilige getallen worden de getallen doorgenomen met alle bijbehorende symboliek.
De studie van het getal is een van de oudste studies ter wereld. Alle wetenschap heeft magie als oorsprong. Elke magiër was op de hoogte van de macht van het getal.
Er wordt in het boek ook aandacht besteed aan vroege telsystemen afkomstig uit Babylon, Soemerië of Oud-Azië, waarin bijvoorbeeld een zestallig systeem gold met totaal andere getalpatronen dan ons tientallige stelsel.
Via het Magisch vierkant belanden we bij de Moderne getallen.
In de laatste 400 jaar is ons getalbegrip sterk getransformeerd. Het getal 0 bijvoorbeeld is door wiskundigen pas na lange aarzeling aanvaard als noodzakelijk. Zelfs theologen huiverden voor dit bijzondere getal. Het is eigenlijk ook geen getal maar slechts een teken voor de afwezigheid van een getal.
Een andere stukje 'magie' was de introductie van de negatieve getallen. Negatieve getallen bleken nuttig te zijn maar creëerden ook een raadsel:
- Het kwadraat van een negatief getal is altijd positief, maar wat is de wortel van een negatief getal?
Wiskundigen beseften, dat er nog een gehele getallenlijn bestond van de wortels van negatieve getallen: de zogeheten imaginaire getallen. Een getal waarvan het kwadraat negatief is, heet imaginair. De wortel uit en imaginair getal is een complex getal, namelijk de som van een reëel getal en een imaginair getal, dat gewoonlijk wordt
weergegeven als de complexe grootheid: a + bi, waarbij:

- i = √-1
- i 2 = -1
- i 3 = -i
- i 4 = 1
- i 5 = i
- i 6 = -1.......
Complexe getallen worden in de wiskunde veelvuldig toegepast, maar ook voor het oplossen van ingewikkelde vraagstukken in bijvoorbeeld de elektrotechniek, zoals het berekenen van kortsluitstromen.
Boek II - Gewijde meetkunde
Dit deel - Boek 2 van het Quadrivium - bevat de elementen van de tweedimensionale meetkunde.
Het verschil met de 'gewone' meetkunde is voornamelijk, dat de bewegingen, concepten en producten symbolische waarde en betekenis worden toegedicht. Zo zouden de studie en de praktijk van de meetkunde de evolutie van de ziel mogelijk maken, net als goede muziek.
Als met een leeg vel papier wordt begonnen, dan is een punt - weergegeven als een rond stipje - het eerst mogelijke. De eerste dimensie - de lijn - ontstaat als het punt iets kiest buiten zichzelf →

Er zijn nu enkele manieren mogelijk om de lijn in het platte vlak te bewegen:
- Het ene deel eind van de lijn - de punt - blijft passief en het andere eind beschrijft een cirkel.
- De actieve punt kan naar een derde positie bewegen op gelijke afstand van de andere twee, waardoor een gelijkzijdige driehoek ontstaat.
- De lijn kan een andere lijn produceren, op een zodanige manier, dat er een vierkant ontstaat.
De basiselementen zijn nu geïntroduceerd.
Via de cirkel en veelvlakken wordt ingegaan op de diverse mogelijkheden, waarbij de gulden snede en de spiraal ook passeren. Ook kerkvensters, en bogen komen langs en de Keltische spiraal.
Boek III - Platonische en Archimedische lichamen
Er zijn vijf 'perfecte' vormen, die vanuit elk van hun hoekpunten dezelfde regelmatige vorm bezitten en waarvan elke ribbe identiek is. Deze veelvlakken of polyeders worden ook genoemd in Plato's Timaeus, waardoor ze vaak Platonische lichamen worden genoemd.
- Het Viervlak of Tetraëder bestaat uit vier gelijkzijdige driehoeken, waarvan er drie bij elk hoekpunt samenkomen
- Het Achtvlak of Octaëder bestaat uit acht gelijkzijdige driehoeken, waarvan er vier op elke hoek samenkomen
- Het Twintigvlak of Icosaëder bestaat uit twintig gelijkzijdige driehoekige vlakken, heeft twaalf hoekpunten en dertig ribben
- De Kubus of Hexaëder is een regelmatig veelvlak, een zesvlak waarvan de zijvlakken vierkanten zijn
- Het Twaalfvlak of Dodecaëder heeft twaalf regelmatige, vijfhoekige vlaken, waarvan en drie op elke hoek samenkomen.

Door combinaties van Platonische lichamen ontstaan weer diverse samengestelde veelvlakken, als Keplerlichamen en Poinsotlichamen.
Een andere groep van lichamen zijn de Archimedische lichamen. Deze halfregelmatige veelvlakken bezitten regelmatige vlakken van meer dan één type en identieke hoekpunten. Deze groep van dertien lichamen worden toegeschreven aan Archimedes, hoewel de beschrijving ervan door Johannes Kepler werd gedaan in zijn Harmonices Mundi. Uitbreidingen en variaties zijn ook bij de Archimedische lichamen aan de orde, waardoor een veelvoud van lichamen ontstaat.
Samen met de Platonische en Archimedische lichamen en de Kepler-Poinsotlichamen vormen ze een verzameling van zo'n 75 veelvlakken. Daaronder vallen veelvlakken met buitengewoon ingewikkelde namen als:
- Romboëdrische kuboctaëder
of:
- Dodecadodecaëder
Boek IV - Harmonograaf
Een op het eerste gezicht wat vreemde eend in het bijt, is de Harmonograaf. In de tijd van het Quadaravium bestond deze nog niet, aangezien deze pas veel later werd uitgevonden.
Een harmonograaf is een mechanisch instrument om twee onafhankelijke - maar op elkaar lijkende - trillingen op de x-as en de y-as van een grafiek uit te zetten. De figuren die zo ontstaan, worden Lissajousfiguren genoemd.
Het toestel werd in het midden van de 19e eeuw gelijktijdig ontwikkeld door verscheidene personen waaronder Jules Antoine Lissajous zelf. Meestal wordt Hugh Blackburn, een wiskundedocent aan de Universiteit van Glasgow, gezien als de ontwikkelaar van het toestel.
De harmonograaf werd gebruikt tot in de 20e eeuw, maar werd al snel verdrongen door de oscilloscoop. Tegenwoordig worden harmonografen enkel nog gebruikt door de echte liefhebbers of om demonstraties te geven. Technische toepassingen heeft het apparaat niet. Het heeft de wiskunde en de muziektheorie wel een breder inzicht gegeven.

Zeer bekend zijn de zogenaamde Lissajousfiguren, die ontstaan als een spiegel achter de punt van een stemvork wordt geplaatst en er een lichtstraal op wordt gericht. Als de stemvork wordt aangeslagen, komt er een verticale lijn tevoorschijn en door zijwaartse reflectie ontstaat dan een sinusgolf. Dit principe is verder uitgewerkt tot een toestel waarmee allerlei variaties mogelijk werden gemaakt.
Een enkelvoudige of laterale harmonograaf maakt gebruik van twee slingers. Eén slinger beweegt een pen heen en weer ten opzichte van een as. De andere slinger beweegt het volledige tekenoppervlak ten opzichte van de loodrechte as. Door het variëren van de frequentie van de slingers ten opzichte van elkaar worden verschillende patronen gecreëerd. Op die manier ontstaan ellipsen, spiralen of complexere Lissajousfiguren op het tekenoppervlak.
Boek V - Muzikale elementen
Muziek wordt door de oren - en ook wel door het lichaam - waargenomen en beleefd door de geest. In muziek structureren en fantaseren we. We rangschikken de elementen - melodie, ritme en harmonie in betekenisvolle vormen en patronen.
Veel van de theorie in Boek V is gebaseerd op de Europese klassieke traditie.
Er wordt in dit boek uitgegaan van de gelijkzwevende stemming, die al meer dan 300 jaar het gangbare stemsysteem vormt.
Verder wordt uitgegaan van de stemtoon of diapason. Dit is in de muziek theorie de toon a' uit het eengestreept octaaf, waarvan de toonhoogte in 1939 in Londen is vastgesteld op 440 Hz. De stemtoon wordt gebruikt voor het onderling op elkaar afstemmen van muziekinstrumenten en is van groot belang voor de bouwers van deze instrumenten en voor de musici die er op spelen.
| Wetenschap | Muziektheorie | Naam | Frequentie (Hertz) |
|---|---|---|---|
| A0 | A" | subcontra | 27,5 |
| A1 | A' | contra | 55 |
| A2 | A | groot | 110 |
| A3 | a | klein | 220 |
| A4 | a' | eengestreept | 440 |
| A5 | a" | tweegestreept | 880 |
| A6 | a"' | driegestreept | 1760 |
| A7 | a"" | viergestreept | 3520 |
| A8 | a""' | vijfgestreept | 7040 |
Een akoestische, piano heeft 88 toetsen, lopend van A" subcontra = 27,5 Hz tot C""' vijfgestreept = 7040 Hz. Van de toetsen zijn er 52 wit en 36 zwart. Hiermee is ook gelijk het hele bereik van alle instrumenten weergegeven, lopend van de Contrafagot tot de Piccolo
Via toonladders, intervallen en baisritmes, passeren instrumentatie en melodische elementen, om uiteindelijk uit te komen bij het bedenken, creëren en componeren van muziek.
Boek VI - Toeval in het zonnestelsel
- 1)De Nederlandse humaniste, theologe en dichteres Anna Maria van Schurman werd in 1636 als eerste vrouwelijke studente in Nederland toegelaten aan de universiteit. Ze moest apart zitten van de anderen, achter een gordijn in een nis, zodat de mannelijke studenten haar niet zagen.
Magisch vierkant
- Een magisch vierkant of tovervierkant is een is een ordening van getallen in een vierkant waarin getallen zodanig zijn ingevuld, dat de kolommen, de rijen en de diagonalen alle dezelfde som opleveren.
Diezelfde som – een constant getal dus – wordt ook wel de magische constante genoemd..
Magische vierkanten zijn een fascinerende manier om getallen te rangschikken, en zijn zeer in populariteit gegroeid, zeker sinds de opkomst van op wiskunde gebaseerde spelletjes als Sudoku.
Oorsprong
Magische vierkanten behoren tot de oudst bekende wiskundige objecten. Als voorbeeld dient het beroemde 3 x 3 magische vierkant, wat volgens legenden uit 2800 voor Christus stamt. Het Lo Shu vierkant - zoals het magische vierkant in China wordt genoemd - is het unieke magische vierkant, waarbij het cijfer 1 aan de onderkant en 2 aan de rechterbovenhoek werd geplaatst.
De magische constante van dit vierkant = 15. De som van alle getallen in het vierkant = 45.
Het Lo Shu vierkant wordt in astrologische kringen ook wel het Saturnesvierkant genoemd.
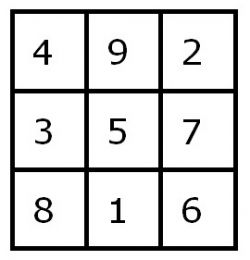
Dit vierkant heeft nog een hogere magische eigenschap, namelijk: 42 + 92 + 2 2 = 82+ 12 + 62 =101, en
42 + 32 + 82 = 22 + 72 + 62 = 89.
Variaties
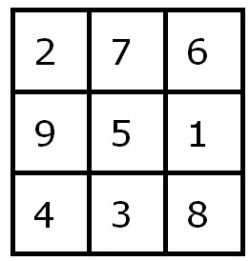
Elk magisch vierkant met drie velden kan worden verkregen uit het Lo Shu vierkant door rotatie of spiegeling. Er zijn namelijk op het Lo Shu vierkant enkele variaties mogelijk. Door kanteling van de rijen verschuiven deze, maar blijft de magische constante = 15 gelijk.
Middeleeuwen
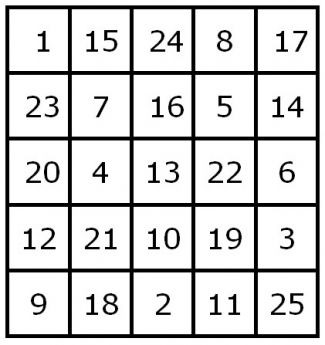
Magische vierkanten waren in de Middeleeuwen geliefkoosde onderwerpen van de rekenkunstenaars en wiskundigen. Gesteld werd, dat een magisch vierkant een vierkant is, dat als een dambord verdeeld is in n2 velden. In die n2 velden zet men de getallen 1, 2,... n2 zodanig, dat zij zowel horizontaal als verticaal, maar ook in de diagonalen steeds dezelfde som geven. Als klassiek voorbeeld uit die tijd werd n = 4 gekozen. Het constante getal van dit vierkant is volgens de geldende rekenkundige reeks:
- 1/2n( n2 + 1 )
waarbij n = aantal velden
Ingevuld wordt dit voor n = 4:
- 2( n2 + 1 ) = 34
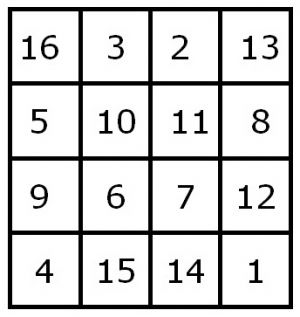
Op de afbeelding is het magische vierkant uit de berekening te zien. Duidelijk is, dat de magische constanten van de rijen en de kolommen en van de twee diagonalen allemaal = 34 zijn, en dat de som van het gehele vierkant volgens de hiervoor geldende rekenkundige reeks:
- ½ a( n2 + 1 ) = 136
waarbij a = alle vierkantjes van het magisch vierkant zijn.
Extra eigenschappen
Ook bij dit vierkant zijn enkele variaties mogelijk. Door kanteling van de rijen verschuiven deze, maar blijft de magische constante gelijk = 34.
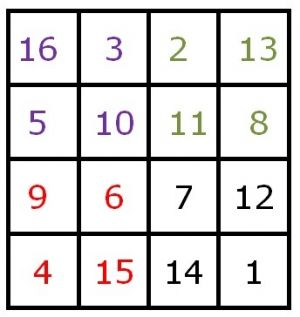
Er zijn nog meer bijzonderheden in het magisch vierkant aanwezig. Als namelijk het vierkant wordt verdeeld in vier vakken, dan is de som van die vier getallen ook steeds 34.
- ( 16 + 3 + 10 + 5 = 34, enz )
Verdere mogelijkheden
De gegeven vierkanten zijn het begin van een reeks magische vierkanten, die steeds ingewikkelder worden. Zo is het eerstvolgende magische vierkant een vierkant met n = 52 velden.
Hierbij is de magische constante:
- 1/2 n( n2 + 1 ) = 2,5( 26 )= 65,
en de som van alle getallen:
- ½ a( n2 + 1 ) = 12,5( 26 )= 325
Ook bij dit magische vierkant zijn allerlei variaties mogelijk.
Naarmate het aantal velden n toeneemt, wordt namelijk ook het aantal variaties groter. Er zijn zelfs magische vierkanten, die driedimensionaal zijn.
Het voert te ver om hier nader op in te gaan.
Bronvermelding
Bronnen, noten en/of referenties:
- Geraadpleegde literatuur: Diverse bronnen en Quadrivium, Rekenkunde, Meetkunde, Muziek en Astronomie voor iedereen. Librero, ISBN:978-90-8998-303-9
Jean Cocteau
Jean Maurice Eugène Clément Cocteau (Maisons-Laffitte, 5 juli 1889 – Milly-la-Forêt, 11 oktober 1963) was een Frans dichter, romanschrijver, toneelschrijver, schilder, ontwerper en filmmaker. Cocteau heeft in zijn leven enorm veel geschreven en geproduceerd, en was thuis in bijna alle kunstvormen en was één van de belangrijkste personen binnen het surrealisme.
Zijn bekendste werken zijn het boek Les Enfants terribles (1929), het toneelstuk Les parents terribles en de film La Belle et la Bête (1946).
Cocteau is een tot de verbeelding sprekend kunstenaar. Maar meer nog dan om zijn werk was Cocteau bekend om zijn opmerkelijke leven. Hij omgaf zich met beroemdheden als Sergei Diaghilev van de Ballets Russes, de zangeres Edith Piaf en de schilder Pablo Picasso, en hij raakte geregeld in opspraak vanwege zijn homoseksualiteit en zijn drugsgebruik.
Afkomst en jeugd
Jean Cocteau, zoon van Georges en Eugénie Cocteau, werd op 5 juli 1889 geboren in Maisons-Laffitte, in het noordwesten van het stedelijk gebied van Parijs. Het echtpaar had al twee kinderen: Marthe, geboren in 1877 en Paul, geboren in in 1881.
Het gezin woonde in de winter samen met hun grootouders van moederszijde in een herenhuis in Parijs en in de zomer in Maisons-Laffitte.
Zijn familie was van een solide Parijse bourgeoisie: gecultiveerd, rijk en geïnteresseerd in muziek, schilderkunst en literatuur. Zijn vader - een jurist - tekent uit liefhebberij en op jonge leeftijd begint Jean dat ook te doen. Zijn grootvader is een muziekliefhebber die muzikale sessies in het huis organiseert.
Jean was een verwend maar nerveus kind. Hij had een grillig karakter en was vaak ziek.
De vroegste herinneringen van Cocteau hadden te maken met het theater in populaire vormen, zoals het circus en het ijspaleis, en met serieuze theaters, zoals de tragedies die werden uitgevoerd bij de Comédie-Française.
Op 5 april 1898 - als Jean 9 jaar oud is - pleegt zijn vader zelfmoord. De reden daarvoor is nooit opgehelderd. Het bleef een duister raadsel dat hem altijd blijft achtervolgen en grote invloed op Cocteau heeft uitgeoefend.
In het voorjaar sterft grootmoeder Lecomte. De grootvader blijft bij zijn dochter wonen. Hij zorgt voor Jean en neemt hem elke zondag mee naar concerten op het conservatorium. Op de Wereldtentoonstelling in Parijs van 1900 is Cocteau vol ontzag voor de dansvoorstellingen.
Na een periode van basisonderwijs - die in alle opzichten onder het gemiddelde lag en vaak werd onderbroken door slechte gezondheid - begint hij zijn eerste jaar op de middelbare school aan de Lycée Condorcet. Hij blinkt uit in slechts drie onderwerpen: tekenen, gymnastiek en Duits. Zijn leraren vinden hem intelligent, maar inconsistent, onoplettend en rusteloos.
Eerste publicaties
De toneelspeler Edouard Max introduceerde de 17-jarige Cocteau in de elitewereld van Parijs. Hij organiseerde een séance rond Cocteaus poëzie, waardoor hij in één keer naam maakte. Zonder hem had Cocteau vast nog een lange weg te gaan gehad door al leurende bij uitgevers aan te kloppen.
Cocteau wordt wel gezien als het product van de jaren onmiddellijk voorafgaand aan de Eerste Wereldoorlog; jaren van verfijnde artistieke smaak, zonder politieke onrust. Er heerste een idealistische en optimistische geest in Europa. Die periode werd ook wel de roaring twenties genoemd.
Zijn echte verkenning van de wereld van het theater begon, toen hij met de Ballets Russes in aanraking kwam, geleid door Sergei Diaghilev. Toen Cocteau de wens uitsprak om balletten te maken, daagde Diaghilev hem uit met: "Etonne-moi" ("Verras me").In 1911 schreef hij het libretto voor Le dieu bleu, een ballet voor de Ballets Russes.
Eerste Wereldoorlog
Toen de Eerste Wereldoorlog bezig was, wilde Cocteau het leger in, maar werd afgekeurd. Hij wist een burgerkonvooi te organiseren om aan de frontlinie gewonden op te halen, waarbij hij als chauffeur fungeerde. Dat hield hij vol tot 1917.
Midden in de oorlog kwam Cocteau met Parade uit, een avant-gardeballet, waarvoor onder anderen Pablo Picasso de decorstukken en de kostuums ontwierp enErik Satie de muziek componeerde. Cocteau en Picasso sloten zich aan bij de groep Ballets Russes van Sergei Diaghilev in Rome om het ballet voor te bereiden. De première van de Parade vond plaats op 18 mei 1917 in het Théâtre de Châtelet. Het publiek en de critici waren meer overbluft dan geërgerd door de muziek van Satie en de sets en kostuums van Picasso. De moderne muziek, het decor, het verhaal; alles was modern en het publiek wist er nog geen raad mee.
Op 12 juli van dat jaar zijn Jean Cocteau, de dichter en schrijver Guillaume Apollinaire en de dichter, schrijver en schilder Max Jacob, getuigen bij het huwelijk van Pablo Picasso en Olga Koklova.
Kritiek
Op een gegeven moment schetst Cocteau in 1919 zijn eigen specifieke kunstgevoel. Ondanks zijn inspanningen om betrokken te worden bij de publicatie van een belangrijk document daarover, wordt Cocteau buitengesloten. In die tijd ook publiceert de schrijver André Gide - een Nobelprijswinnaar - een open brief aan Jean Cocteau in de Nouvelle Revue française waarin hij de dichtbundel Le Cap de Bonne-Espérance (Kaap de Goede Hoop) en het ballet Parade bekritiseert. In hetzelfde artikel citeert Gide Le Coq et le Arlequin (De haan en de harlekijn) als bewijs dat de dichter geen muzikale vaardigheden bezit. Cocteau reageert hierop fel in het literaire tijdschrift Les Ecrits nouveaux , waarop Gide natuurlijk terugschiet. Voor Cocteau sluit deze vervelende polemiek tijdelijk de deur naar de Nouvelle Revue française , waarvoor hij bijdragen leverde.
Productie
In 1920 ontmoet hij de zestienjarige Raymond Radiguet, wat uitgroeit tot een liefdesverhouding. In datzelfde jaar wordt Cocteau de verdediger en grote inspirator van jonge musici, die al snel bekendheid verwerven als de "Groupe de Six".
Hij brengt juni en het grootste deel van juli door in Londen met Darius Milhaud om de Engelse productie van Le Bœuf sur le toit in het London Coliseum te verfijnen.
In oktober komt Cocteau uit met het boek Thomas l'imposteur (Thomas de bedrieger), waar in 1964 ook een film van is gemaakt.
Op 12 december sterft Radiguet bij gebrek aan onvoldoende medische begeleiding aan tyfus. De totaal ingestorte Cocteau woont de begrafenis niet bij.
Enige tijd later nemen Serge Diaghilev, Auric en Poulenc een radeloze Cocteau mee naar Monte-Carlo. Ze geven hem de raad om troost te zoeken in de opium, wat bij Cocteau tot verslaving leidt. Intussen werkt hij aan plannen voor het ballet Le Train bleu.
In 1925, ondergaat Cocteau - op aandringen van vrienden - een behandeling voor zijn opiumverslaving in de Clinique des Thermes Urbains.
Een periode van intense creativiteit volgt waarin veel werk van hem wordt gepubliceerd. In het jaar daarna schrijft hij het libretto voor de opera-oratorium Oedipus Rex voor Stravinsky die vanaf half januari aan de muziek werkt. In mei 1927 was de première, waarbij het werk niet onverdeeld gunstig werd ontvangen.
In december vond in de Galerie des Quatre Chemins een tentoonstelling van ongewone objecten en tekeningen plaats met de titel Poésie plastique (Gebeeldhouwde poëzie). Het was een eerste pogingen van Cocteau tot creatie van een moderne post-kubistische kunst in Frankrijk
Op 16 december 1927 première van de opera Pauvre matelot (The Poor Sailor), met muziek van Darius Milhaud. Cocteau voltooit La voix humaine (The Human Voice) en schrijft Le Livre blanc (The White Book). Op 28 december gaat de opera Antigone in première in het Théâtre de la Monnaie in Brussel met muziek van Honegger.
Eind november 1928 checkt hij in bij een kliniek in Saint-Cloud in voor een nieuwe poging tot afkicken. 1929 Maakt tekeningen, begint aan het boek Opium, journal d'une désintoxication en schrijft in drie weken Les Enfants terribles (Children of the Game), dat zeer gunstig wordt ontvangen. In het boek Opium beschrijft Cocteau's het herstel van zijn verslaving aan opium. Eind augustus 1931 blijkt hij besmet te zijn met tyfus en moet hij veertig dagen in een kliniek doorbrengen. Kort daarop begon hij weer met opium te roken. In 1933 ondergaat hij weer een kuur om daar van af te raken. Terwijl ze audities houden voor Oedipus Rex, merkt Cocteau Jean Marais op, en geeft hem een rol in het koor.1938, Jean Marais speelt Galahad in Les Chevaliers de la Table ronde
1)Le train bleu is een ballet van één acte, gechoreografeerd door Bronislava Nijinska op muziek van Darius Milhaud voor Serge Diagilevs Ballets Russes, gebaseerd op een scenario van Jean Cocteau. De titel was afkomstig van de nachttrein genaamd Le Train Bleu, die rijke passagiers van Calais naar de Middellandse Zee vervoerde. Le Train bleu beleefde zijn première op 20 juni 1924.
| Frederick Delius I | ||
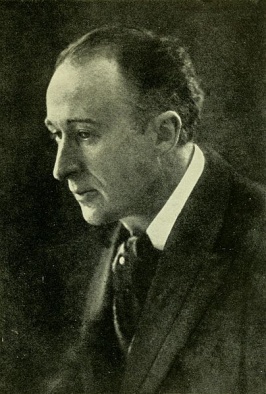
| ||
| Frederick Delius 45 jaar (1907) | ||
| Algemene informatie | ||
| Volledige naam | Frederick (Fritz) Theodor Albert Deliubij het huwelijk tussens | |
| Geboren | 29 januari 1862, Bradford | |
| Overleden | 10 juni 1934, Grez-sur-Loing | |
| Nationaliteit | Engels | |
| Beroep | Componist | |
Frederick Delius (Bradford, 29 januari 1862 – Grez-sur-Loing, 10 juni 1934)
was een Engels componist en zoon van een succesvolle wolhandelaar van Duitse afkomst.
Frederick Delius begon op jonge leeftijd piano te spelen, als autodidact. Later kreeg hij van zijn vader toestemming om vioolles en pianolessen te volgen, maar maar deze vond het beroep van musicus eigenlijk beneden zijn stand. Hij benadrukte ook sterk, dat muziek enkel geschikt was voor ontspanning en plezier en dat er geen geld mee viel te verdienen.
Soort muziek
De nogal ingetogen muziek van Delius is niet voor iedereen toegankelijk. Om die reden werd hij dan ook pas laat in zijn leven in Engeland gewaardeerd.
In Delius's vaderland - Groot-Brittannië – werd zijn muziek pas na 1907 geregeld in concertprogramma's vermeld, nadat de dirigent Thomas Beecham (later sir Thomas Beecham) het voor hem opnam. Thomas Beecham zette zich zijn gehele dirigentencarrière onvermoeibaar in om werken van Delius uit te voeren.
De muziek van Delius is slechts af en toe populair geweest en vaak onderhevig aan kritieke aanvallen.
Ook in Duitsland werden en worden zijn werken bijna niet uitgevoerd: slechts enkele klassieke liefhebbers kennen ze.
Een kenmerkend element in zijn werk is de schoonheid - vooral van de natuur, weelderige bloemen en tuinen – speciaal gezien in het licht van vergankelijkheid, herfst, verval en verwelking.
Zijn meest bekende orkestwerk, dat vrij vaak te horen valt is:
- On hearing the First Cuckoo in Spring.
Muzikale ontwikkeling
| Dit is een artikel uit de serie: Bekende melodie, onbekende componist |
|---|
Delius werkte enige tijd in de wolhandel maar had daar een grondige hekel aan. Zijn vader kocht daarop voor hem een sinaasappelplantage in Florida. Daar leerde hij de organist Thomas Ward kennen, die hem tijdje uitgebreid les in compositie gaf. Hier kwamen ook zijn eerste composities tot stand. Daarna bracht hij een paar maanden door in Danville, Virginia, waar hij geld verdiende met orgelspelen, zingen en lesgeven.
Uiteindelijk lukte het hem dan ook zijn vader te overtuigen, dat muziek zijn richting was. In 1886 stond zijn vader hem toe gedurende anderhalf jaar een muziekcursus te volgen in Duitsland aan het Leipziger Konservatorium. Daar ontmoette hij onder meer Edvard Grieg , die zijn familie ook nog eens duidelijk maakte, dat Frederick voor de muziek bestemd was.
Zelfstandig componist
Na zijn studie vestigde Delius zich in Parijs en begon hij aan een fulltime carrière als componist. Gedurende zijn verblijf in Parijs werd zijn werk echter weinig uitgevoerd. Hij werd onderhouden door zijn vader, die hem geregeld geld opstuurde. Wel werden zijn eerste werken uitgegeven, zoals de Suite Florida, twee strijkkwartetten en enige liederen.
In 1897 In 1897 ontmoette Delius de Duitse kunstenares Jelka Rosen. Ze was een professionele schilder, een vriend van de beeldhouwer Auguste Rodin, en een vaste exposant in de Salon des Indépendants. Jelka liet al snel haar bewondering blijken voor de muziek van de jonge componist en het paar groeide verder naar elkaar. Dit werd nog versterkt door een gedeelde passie voor het werk van de Duitse filosoof Friedrich Nietzsche en de muziek van Edvard Grieg.
Delius trouwde met Jelka Rosen, waarna ze intrek namen in Grez-sur-Loing bij Fontainebleau, waar ze tot hun dood zouden blijven wonen.

Delius vermeed de omgang met andere musici, maar was wel bevriend met de schrijver August Strindberg en de schilders Paul Gauguin en Edvard Munch.
In 1913 ging zijn compositie On Hearing the First Cuckoo in Spring met veel succes in prèmiere. Van alle werken die Delius geschreven heeft, is dit wel het meest bekende geworden.
|
De compositie On Hearing the First Cuckoo in Spring is een symfonisch gedicht gecomponeerd in 1912 door Frederick Delius, en is een puur instrumentaal werkje.
|
Eerste successen
In het begin van 1900 kwam Delius tot een vruchtbare samenwerking met Duitse liefhebbers aanhangers van zijn muziek, namelijk de dirigenten Hans Haym, Fritz Cassirer, Alfred Hertz in Elberfeld, en Julius Buths in Düsseldorf.
Hans Haym dirigeerde het orkestwerk Over the Hills and Far Away, die hij op 13 november 1897 onder de Duitse titel Über die Berge in die Ferne gaf. Dit was de eerste keer dat Delius's muziek in Duitsland werd gehoord. In 1899 gaf Alfred Hertz een concert van muziek van Delius in de St. James's Hall in Londen, waaronder ook weer Over the Hills and Far Away, een koorwerk en fragmenten uit de opera Koanga.
Het was uitzonderlijk, dat een onbekende componist - in een tijd waarin een orkestconcert een zeldzame gebeurtenis was in Londen - die gelegenheid kreeg. Ondanks bemoedigende kritieken, werd de orkestrale muziek van Delius tot 1907 niet in een Engels concertgebouw meer gehoord. De meeste premières van Delius uit deze periode werden gegeven door Hans Haym en andere Duitse dirigenten.
Rond 1907, was - dankzij de uitvoeringen van zijn werken in veel Duitse steden - Delius, zoals Thomas Beecham zei, "veilig ronddrijvend op een golf van succes die toenam naarmate de tijd vorderde".
Moeilijke tijden
Vanaf 1914 begon een slechte tijd voor Delius toen het Verenigd Koninkrijk aan Duitsland de oorlog verklaarde. Zijn werken werden in Duitsland - waar veel van zijn werken hun eerste uitvoering kregen - niet meer gespeeld en zo verloor hij een groot deel van zijn inkomsten. Zij besloten toen naar Engeland te emigreren, naar een tijdelijk verblijf in het zuiden van Engeland.
Uit die tijd stammen een vioolsonate, een strijkkwartet, het vioolconcert, het celloconcert en het dubbelconcert voor viool en cello.
Andere werken van deze jaren, zoals het Requiem (1914-1916), waren minder succesvol.
Ziekte
In de jaren 20 kwam de syfilis – opgelopen tijdens zijn periode in Parijs - in een stadium, waarbij verschillende organen werden aangetast, waardoor Delius voor zijn verdere leven verlamd werd en blind werd. Zijn tweede vioolsonate (1923) moest zijn vrouw Jelka opschrijven. Daarna stond zijn compositorische activiteit enkele jaren stil.
In 1928 leerde hij de jonge musicus en bewonderaar Eric Fenby kennen, die vanaf toen de ernstig zieke componist bijstond tot aan zijn dood. Hij nam waar, dat Delius probeerde te componeren door te dicteren aan Jelka, waarop hij zijn diensten aanbood als een onbetaalde amanuensis. Gedurende vijf jaar werkte hij samen met Delius, zette zijn nieuwe composities op papier - waaronder de derde vioolsonate - en hielp hem zijn eerdere werken te herzien.
Laatste jaren
Frederick Delius overleed in Grez-sur-Loing op 10 juni 1934, 72 jaar oud. Hij wilde in zijn eigen tuin worden begraven, maar dat werd verhinderd door de Franse autoriteiten. Zijn alternatieve wens was, - ondanks zijn atheïsme – dat hij zou begraven worden "op een of ander kerkhof in het zuiden van Engeland, waar mensen wilde bloemen kunnen planten". Zijn vrouw Jelka was te ziek om de reis over het kanaal te maken, zodat Delius tijdelijk werd begraven op de plaatselijke begraafplaats in Grez-sur-Loing.
In mei 1935 vond Jelka dat ze genoeg kracht had om de oversteek te maken om een herbegrafenis in Engeland bij te wonen. Ze koos St. Peter's Church, Limpsfield, Surrey als de plek voor het graf. Ze voer naar Engeland voor de dienst, maar werd onderweg ziek en werd bij aankomst naar het ziekenhuis in Londen gebracht, en miste op die manier de herbegrafenis op 26 mei. Jelka stierf twee dagen later op 28 mei. Ze werd begraven in hetzelfde graf als Delius.
Bronvermelding
Bronnen, noten en/of referenties:
- On hearing the first Cuckoo in Spring van Frederick Delius op YouTube
- Delius Society. De Delius Society, opgericht in 1962 door zijn meer toegewijde volgelingen, blijft de kennis van het leven en werken van de componist bevorderen en sponsort de jaarlijkse The Delius Prize voor jonge muzikanten.
Adolphe Adam
| Adolphe Adam | ||

| ||
| Adolphe Adam in 1840 | ||
| Achtergrondinformatie | ||
| Volledige naam | Adolphe Adam | |
| Geboren | 24 juli 1803 | |
| Overleden | 3 mei 1856 | |
| Origine | ||
| Genre(s) | Klassiek | |
| Beroep(en) | Componist, dirigent, docent | |
Adolphe Adam ((Parijs), 24 juli 1803 – Berlijn, 3 mei 1856)
was een Frans componist, pianist, muziekpedagoog en muziekcriticus. Tijdens zijn leven had hij veel succes, vooral als componist maar ook als docent.
Adolphe Adam componeerde een groot aantal muziekstukken, die echter geen repertoire hebben gehouden, met uitzondering dan van de ouverture Si j'étais roi, en het ballet Giselle dat nog geregeld wordt uitgevoerd.
| Dit is een artikel uit de serie: Bekende melodie, onbekende componist |
|---|
Opleiding
De Franse componist Adolphe Adam (1803-1856) werd geboren in Parijs. Zijn vader – Johann Ludwig Adam, afkomstig uit de Elzas – was componist, pianist en pianoleraar aan het Conservatoire de Paris. Alhoewel Adolphe een groot muzikaal talent had, wilde zijn vader niet dat hij die kant opging, maar hij ging toch muziek studeren zonder dat zijn ouders daar iets van wisten.
Op veertienjarige leeftijd werd hij als 'amateur' toegelaten tot het Conservatoire de Paris in Parijs, op voorwaarde, dat hij nooit theatermuziek zou gaan schrijven. Daar is in de praktijk niet veel van terecht gekomen.
Talrijke composities
Adolphe Adam was tijdens zijn leven zeer populair. Hij schreef voornamelijk opera's en balletten.
De eerste compositie die Adam schreef, was een komische opera Pierre et Catherine. Deze opera werd opgevoerd in Parijs in 1829. Een jaar later volgde Danilowa.
Adolphe Adam bedacht met groot gemak nieuwe melodieën en de orkestratie daarvan ging hem ook gemakkelijk af. Zijn volgende opera's waren eveneens zeer succesvol.
De muziek die hij schreef bij de balletten, werd niet alleen in Parijs, maar ook in Berlijn, Londen en St. Petersburg opgevoerd.
Een van zijn bekendste balletten is Giselle uit 1841 dat nog vaak wordt uitgevoerd.
|
Adolphe Adam was een componist, die tijdens zijn leven veel succes had met zijn muziek. Van al zijn werk wordt tegenwoordig niet veel meer uitgevoerd. Wel houdt zijn ballet Giselle nog steeds repertoire. Een ander muziekstuk - de ouverture Si j'étais roi - is ook nog geregeld in de concertzaal te horen. De bijbehorende opera wordt echter nog maar zelden uitgevoerd. In de ouverture Si j'étais roi volgen een paar thema's elkaar vloeiend op, te beginnen met een stevige inzet van het orkest in 2/4-maat, overgaand in meer melodieuze muziek en vervolgd door - wat lijkt - op een Perzische dans. |
Si j'étais roi
In 1852 schreef Adolphe Adam schreef de muziek voor de opéra-comique Si j’étais roi (Als ik Koning zou zijn).
Het libretto werd geschreven door Adolphe d’Ennery und Jules-Henri Brésil. Het is een opera in drie aktes geworden, die tot de Franse Romantiek wordt gerekend.
Het werk beleefde zijn prèmiere op 4 september 1852 in het Théâtre-Lyrique in Paris. De opera was zeer succesvol en beleefde een groot aantal opvoeringen. Ook in andere landen werd de opera met gejuich ontvangen. In Duitsland bijvoorbeeld kwam deze uit onder de titel: Wenn ich König wär’.
- De handeling speelt zich af in begin 1600 in een fantastisch koninkrijk, dat dicht bij zee ligt. De arme visser Zéphoris redt het leven van een meisje – Néméa - dat bijna verdronk. Hij denkt nog steeds aan haar, ook omdat hij graag de kostbare ring wil teruggeven die bij haar redding van de vinger was gegleden. Toevallig komt op een dag koning Moussol, voorbij en ziet, dat de visser iets in het zand heeft geschreven, namelijk:
- ALS IK KONING ZOU ZIJN
- Dit brengt de koning op het idee de visser voor één dag koning te laten zijn. Dit gebeurt dan ook, met als resultaat de meest wonderlijke taferelen en – zoals het hoort - met een goede afloop voor Zéphoris die in de adelstand wordt verheven en mag trouwen met Néméa, de dochter van koning Moussol.
Théâtre National
Adolphe Adam was ondernemend genoeg. Toen hij in 1847 ruzie kreeg met de directie van de Opéra Comique, ging hij niet bij de pakken neerzitten maar opende op eigen kosten het Théâtre National,waar vooral het werk van jonge componisten werd opgevoerd. De revolutie van 1848 maakte een eind aan deze onderneming, omdat Adam al zijn spaargeld was kwijtgeraakt.
In 1849 werd Adam aangesteld als compositieleraar aan het conservatorium in Parijs.
Persoonlijke leven
Adolphe Adam trouwde in 1829 met de actrice Sara Lescot, met wie hij een zoon had, Adrien-Leopold Adam (1832-1851). Na de dood van zijn vrouw in 1851 trouwde hij metde zangeres Cherie Louise Couraud.
Adolphe Adam werd slechts 52 jaar oud, en werd begraven op het Cimetière de Montmartre in Parijs, waar ook Léo Delibes en Heinrich Heine hun laatste rustplaats hebben gevonden.
Tijdens zijn relatief korte leven schreef Adam meer dan vijftig opera's, vijftien balletten en talloze producties voor de Parijse vaudevilletheaters.
Bronvermelding
Bronnen, noten en/of referenties:
Nicolas Eustache Maurin - Dit bestand is geëxtraheerd uit een ander bestand: Adolphe Adam by Maurin.jpg
Afgebeelde persoon: Adolphe Adam 1840 Artist
Nicolas Eustache Maurin (1799–1850)
| Dit is een artikel uit de serie: Bekende melodie, onbekende componist |
|---|
| Dit is een artikel uit de serie: Bekende melodie, onbekende componist |
|---|
| Dit is een artikel uit de serie: Bekende melodie, onbekende componist |
|---|
||i=1 |}
Ψ (x⃗,t)
De stad Montfort-L'Amaury in eerbetoon aan Maurice Ravel die in dit huis van 1921 tot 1937 woonde Ravel se fixa à Montfort-l'Amaury en 1921. Sa maison, le Belvédère, conservée en l'état selon la volonté de son frère, abrite un musée depuis 1971 et fait l’objet d’une inscription auprès des monuments historiques depuis 199459. Français : Maison dite du Belvédère de Maurice Ravel à Montfort-l'Amaury (Yvelines, France) Date 20 November 2006 Source Cliché personnel, own work Author ℍenry Salomé (Jaser !) 08:17, 21 November 2006 (UTC) Object location 48° 46′ 34.28″ N, 1° 48′ 19.4″ E Kartographer map based on OpenStreetMap. View this and other nearby images on: OpenStreetMap - Google Earth info Licensing[edit] The copyright holder of this work, hereby publish it under the following licenses: GNU head Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.
- OPVS FUNDATUM VATICANVM
- Josephvs Ratzinger - Benedictvs XVI
- - Cooperatores Veritatis -
- OPUS FUNDUM VATICANUM
- Josephus Ratzinger - Benedictus XVI
- - Cooperatores Veritatis -
|
|
span>
- Ook in de bioscoop werden antifascistische acties uitgevoerd
|}
Enkele breuken hebben een eigen naam:
- √12
≈12 1 1 = 1
- 2 0 12 = 1
- 2 1 12 = 1,059463094
- 2 2 12 = 1,122462048
x 4
√ L C
|
|
|
|
|
|
|
|
| Op een gegeven moment stelt hij vast,
dat het een verloren zaak is. |
|---|
|
|
- Het schrijven van de Magister Ludi aan de Pedagogische Dienst
|}
|
|
|
|
{{Overline| (12)}}om ergens een lijntje boven te trekken{{Overline|24}}
12
24
12
--
24
Breuken
Bestand:Rmath.png

a b⁄c: a b/c (geheel getal, teller en noemer)
a⁄b: a/b (teller en noemer)
1⁄a: 1/a (alleen noemer)
12
--
24
{{Overline|a}}
12
24
a
{{Overline|24}}
12
24
Sjabloon:I =vbreuk
In deze theoretische verhandeling, wordt de vergelijking:
S = A L geïntroduceerd.
Hierbij is:
- S de stroom
- A de spanning
- L de weerstand
Later zijn deze letters vervangen door de huidige notatie: I = U R
sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = sin 32,3122 0 = 0,5345 24
Schrijfwijze
Het hoofdtelwoord geeft de teller van een breuk weer, het rangtelwoord de noemer.
- 1 5 een vijfde, 7 10 zeven tiende, 1 2 6 een twee zesde.
- 11 1 5 elf en een vijfde, elf een vijfde, of elf gehelen en een vijfde.
Enkele breuken hebben een eigen naam:
Een derde lijkt een eigen naam te hebben. Het is als breuk een "gewone" combinatie (derde is het rangtelwoord van drie):
- 1 3 een derde (dus niet eenderde)
- 2 3 twee derde.
sina cosa
- 30-10 5
60 24/60
- Rv = 1 1R1 + R2 +......Rn
1 5
- x(t)
x→(t) = v→ • t + x0→ = dx→ dt • t + x0→
y(p) x(p) = K • G(p) 1 + [K • G(p) • H(p)]
sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = 0 = 0,5345 24
sin a = sin 32 + 18 + 44 60/60 = sin 32,3122
Het eerste voorbeeld is ook als volgt toe te lichten: als men twee taarten elk in vier even grote stukken snijdt, resulteert dat in acht stukken. Ook het delen van breuken is zo te beschrijven: als men anderhalve (1 1⁄2 = 3⁄2) euro uitgeeft aan artikelen die een halve euro per stuk kosten, krijgt men drie van die artikelen, want 3 2 : 1 2 = 3 2 × 2 1 = 3 × 2 2 × 1 = 3.
Groter
|
Op een gegeven moment meent hij, dat hij de zin van het Spel dicht is genaderd, maar denkt toch dat hij dit niet tot zijn beroep moet maken. |
23 • 60 • 60 = 82.800
128 4/ 7 0 achtenveertig achtenveertig
- P = U • I • cos φ
- P = 3U f • I f • cos φ
waarbij:
- U f = U fase en I f = I fase
- P = 3 U fase• I fase • cos φ
- Moon River, Goodnight Moon, Moon Cloud, Dark of the Moon

- Δ BCD ~ Δ ABC
Franciscus 7 feb 2015 12:31 (CET)
- Pagina's met dubbele sjabloonparameters
- Rekenkunde
- Wiskunde
- Getal
- Cijfer
- Artikel Luisterrijk
- Geboren in Bradford
- Geboren op 29 januari
- Geboren in 1862
- Overleden in Grez-sur-Loing
- Overleden op 10 juni
- Overleden in 1934
- Engels componist
- Componist
- Frankrijk
- Geboren in (Parijs)
- Geboren op 24 juli
- Geboren in 1803
- Overleden in Berlijn
- Overleden op 3 mei
- Overleden in 1856
- Frans componist
- Pianist
- Literatuur
- Tijdschrift
- Literair genre
- Vakliteratuur
- Pagina's met onjuiste bestandskoppelingen
