Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Essay:Kunst en Wiskunde I: verschil tussen versies
Geen bewerkingssamenvatting |
|||
| (25 tussenliggende versies door 4 gebruikers niet weergegeven) | |||
| Regel 3: | Regel 3: | ||
Wat onderga je, als je als bezoeker in een museum op de vloer een groot aantal blinkende staven ziet liggen? | Wat onderga je, als je als bezoeker in een museum op de vloer een groot aantal blinkende staven ziet liggen? | ||
<br/>De een zal er even naar kijken, er geen raad mee weten en verder lopen. De ander zal wat meer belangstelling tonen en op onderzoek uitgaan. | <br/>De een zal er even naar kijken, er geen raad mee weten en verder lopen. De ander zal wat meer belangstelling tonen en op onderzoek uitgaan. | ||
<br/>Het is in ieder geval zó, dat deze uitstalling de meeste mensen niet geheel onverschillig laat, en dat minstens je nieuwsgierigheid wordt gewekt. Misschien dringt zelfs de achterliggende | <br/>Het is in ieder geval zó, dat deze uitstalling de meeste mensen niet geheel onverschillig laat, en dat minstens je nieuwsgierigheid wordt gewekt. Misschien dringt zelfs de achterliggende gedachte aan je op, dat hier iets bijzonders aan de hand is. | ||
==Vloersculptuur== | ==Vloersculptuur== | ||
[[Afbeelding:Staven Walter De Maria.jpg|370px|right]] | [[Afbeelding:Staven Walter De Maria.jpg|370px|right]] | ||
Het werk op de afbeelding – een indrukwekkend vloersculptuur - is door de Amerikaan '''Walter De Maria''' (1935-2013) in 1984 gemaakt in opdracht van ''Museum Boymans – Van Beuningen'' in Rotterdam. De naam die de kunstenaar aan dit werk meegaf luidt: ''A Computer Which Will Solve Every Problem in the World'' (Een computer die elk probleem in de wereld zal oplossen). | |||
<br/>Het werk bestaat uit '''75 gepolijste roestvast stalen staven''', die in rijen op de vloer zijn neergelegd en die elk precies '''een meter''' lang zijn. | <br/>Het werk bestaat uit '''75 gepolijste roestvast stalen staven''', die in rijen op de vloer zijn neergelegd en die elk precies '''een meter''' lang zijn. | ||
<br/>Bij een eerste verkenning valt je onmiddellijk op, dat de heldere en gelijkmatige opbouw van de vloersculptuur bij iedere verandering van standpunt een nieuw beeld oplevert. | <br/>Bij een eerste verkenning valt je onmiddellijk op, dat de heldere en gelijkmatige opbouw van de vloersculptuur bij iedere verandering van standpunt een nieuw beeld oplevert. | ||
<br/>In de rangschikking op de vloer blijkt een strikte ordening te heersen, die | <br/>In de rangschikking op de vloer blijkt een strikte ordening te heersen, die | ||
zich pas na enig zoeken en nadenken prijsgeeft. Het blijkt, dat - beginnend met een rij van '''drie''' '''driehoekige''' staven – de sculptuur eindigt in een rij van '''twaalf''' - bijna ronde - '''twaalfhoekige''' staven. Alle rijen staven blijken dus opgebouwd te zijn uit steeds oplopende regelmatige | zich pas na enig zoeken en nadenken prijsgeeft. Het blijkt, dat - beginnend met een rij van '''drie''' '''driehoekige''' staven – de sculptuur eindigt in een rij van '''twaalf''' - bijna ronde - '''twaalfhoekige''' staven. Alle rijen staven blijken dus opgebouwd te zijn uit steeds oplopende regelmatige [[Meetkunde ( Veelhoeken )| | ||
veelhoeken]]<sup> 1)</sup>. | |||
<br/>In deze rangschikking liggen er dus tien rijen in een bijbehorend patroon, waarbij dus - naarmate de rijen opschuiven – het aantal facetten van de staven stijgt, waardoor steeds meer de vorm van een [[Rondom de cirkel ( 2 )|cirkel]] wordt benaderd. | <br/>In deze rangschikking liggen er dus tien rijen in een bijbehorend patroon, waarbij dus - naarmate de rijen opschuiven – het aantal facetten van de staven stijgt, waardoor steeds meer de vorm van een [[Rondom de cirkel ( 2 )|cirkel]] wordt benaderd. | ||
De lengte van '''een meter''' is aanwezig in de gehele opstelling: ook de evenwijdige rijen bevinden zich steeds op '''een meter''' van elkaar. | De lengte van '''een meter''' is aanwezig in de gehele opstelling: ook de evenwijdige rijen bevinden zich steeds op '''een meter''' afstand van elkaar. | ||
------------------------------------------------ | ------------------------------------------------ | ||
<sup> 1)</sup> ''Regelmatige veelhoeken zijn tweedimensionale meetkundige figuren, bestaande uit een eindig aantal lijnstukken ( zijden ) die alle dezelfde lengte hebben, en waarvan alle hoeken even groot zijn. '' | <sup> 1)</sup> ''Regelmatige veelhoeken zijn tweedimensionale meetkundige figuren, bestaande uit een eindig aantal lijnstukken ( zijden ) die alle dezelfde lengte hebben, en waarvan alle hoeken even groot zijn. '' | ||
==Herhaling== | ==Herhaling== | ||
De kracht van het kunstwerk zit voor een deel in de ''herhaling'', met steeds een subtiele toevoeging. De herhaling heeft hier betrekking op: | De kracht van het kunstwerk zit voor een deel in de ''herhaling'', met steeds een subtiele toevoeging. De herhaling heeft hier betrekking op: | ||
{{infobox}} | |||
| | |||
<span> | |||
<font> | |||
:<span style="font-size:150%;"><font color=blue>''De kracht van het kunstwerk zit voor een deel in de herhaling'' | |||
</font> | |||
<span> | |||
|} | |||
:* dezelfde lengte van de staven | :* dezelfde lengte van de staven | ||
:* het gelijke oppervlak van alle staven | :* het gelijke oppervlak van alle staven | ||
| Regel 32: | Regel 41: | ||
De vloersculptuur werd door ''Walter De Maria'' ontworpen in 1984, voordat computers uitgroeiden tot de allesomvattende apparaten die ze tegenwoordig zijn. | De vloersculptuur werd door ''Walter De Maria'' ontworpen in 1984, voordat computers uitgroeiden tot de allesomvattende apparaten die ze tegenwoordig zijn. | ||
<br/>Walter De Maria was er zich er natuurlijk van bewust, dat computers in staat zijn nogal wat economische en technische problemen op te lossen, maar dat er zich in het leven andere opgaven en problemen voordoen die buiten het bereik van computers vallen en dus hierdoor ook niet kunnen worden opgelost. | <br/>Walter De Maria was er zich er natuurlijk van bewust, dat computers in staat zijn nogal wat economische en technische problemen op te lossen, maar dat er zich in het leven andere opgaven en problemen voordoen die buiten het bereik van computers vallen en dus hierdoor ook niet kunnen worden opgelost. | ||
< | {{infobox}} | ||
| | |||
<span> | |||
<font> | |||
:<span style="font-size:150%;"><font color=blue>''Antwoorden op problemen kunnen niet altijd op een logische of rationele manier worden benaderd'' | |||
</font> | |||
<span> | |||
|} | |||
De badinerende titel: ''A Computer Which Will Solve Every Problem in the World'' die hij aan het kunstwerk meegaf, geeft dus aan, dat voor hem de antwoorden op problemen niet altijd op een logische of rationele manier kunnen worden benaderd, maar dat er ook andere wegen zijn als een verhoogd bewustzijn via waarneming of intuïtie, zeker als het om de kunst gaat. | |||
<br/> In de poëzie kom je hetzelfde tegen, vooral in de moderne poëzie. Sommige teksten zijn namelijk op het eerste gezicht niet altijd even logisch, maar het op je laten inwerken en de atmosfeer ervan proeven is dikwijls al voldoende. De Vlaamse dichter [[Paul van Ostaijen]] (1896 -1928 ) is hier een duidelijk voorbeeld van. In zijn gedicht '''VORST''' mis je de logica, maar proef je het gevoel. | <br/> In de poëzie kom je hetzelfde tegen, vooral in de moderne poëzie. Sommige teksten zijn namelijk op het eerste gezicht niet altijd even logisch, maar het op je laten inwerken en de atmosfeer ervan proeven is dikwijls al voldoende. De Vlaamse dichter [[Paul van Ostaijen]] (1896 -1928 ) is hier een duidelijk voorbeeld van. In zijn gedicht '''VORST''' mis je de logica, maar proef je het gevoel. | ||
<br/> | <br/> | ||
| Regel 56: | Regel 73: | ||
<br/> | <br/> | ||
<br/>Ook in de schilderkunst kom je op hetzelfde vlak uit. De Nederlandse schilders als [[Piet Mondriaan]] en [[Theo van Doesburg]] hielden zich bezig met puur geometrische figuren waarvan alle vormen zijn teruggebracht tot het uiterste met een beperkt kleurgebruik. Ook schilders als [[Kassimir Malevich]] en [[El Lissitzky]] waren op soortgelijke wijze bezig. | <br/>Ook in de schilderkunst kom je op hetzelfde vlak uit. De Nederlandse schilders als [[Piet Mondriaan]] en [[Theo van Doesburg]] hielden zich bezig met puur geometrische figuren waarvan alle vormen zijn teruggebracht tot het uiterste met een beperkt kleurgebruik. Ook schilders als [[Kassimir Malevich]] en [[El Lissitzky]] waren op soortgelijke wijze bezig. | ||
==Is het kunst?== | ==Is het kunst?== | ||
De vloersculptuur van Walter De Maria wordt gerekend tot het '''Minimalisme'''. | De vloersculptuur van Walter De Maria wordt gerekend tot het '''Minimalisme'''. | ||
| Regel 64: | Regel 82: | ||
<br/>Dat kunst iets bijzonders inhoudt, lijkt niet ter discussie te staan. Veel mensen hebben grote waardering voor de kunst, ook voor de moderne kunst die voorop loopt in het onderzoeken en vergroten van ons bewustzijn, en die soms provocerend kan zijn. | <br/>Dat kunst iets bijzonders inhoudt, lijkt niet ter discussie te staan. Veel mensen hebben grote waardering voor de kunst, ook voor de moderne kunst die voorop loopt in het onderzoeken en vergroten van ons bewustzijn, en die soms provocerend kan zijn. | ||
<br/>Er is een heldere uitspraak van de Amerikaanse kunstenaar '''Robert Irwin''', die aangeeft, dat: | <br/>Er is een heldere uitspraak van de Amerikaanse kunstenaar '''Robert Irwin''', die aangeeft, dat: | ||
:* ''Kunst een continu onderzoek is van | :* ''Kunst een continu onderzoek is van ons op waarneming gebaseerde bewustzijn, en is een continue verruiming van de ons omringende wereld''. | ||
Deze uitspraak lijkt bijna geheel van toepassing op het sculptuur van Walter De Maria. We onderzoeken en vergroten ons bewustzijn bij het waarnemen en laten inwerken van de sculptuur op je en het ontdekken van patronen in de opstelling. | Deze uitspraak lijkt bijna geheel van toepassing op het sculptuur van Walter De Maria. We onderzoeken en vergroten ons bewustzijn bij het waarnemen en laten inwerken van de sculptuur op je en het ontdekken van patronen in de opstelling. | ||
<br/>Je kunt ook over kunst praten en nadenken op een heel andere manier. Kunst kan ook een bron van kennis zijn net als de wetenschap dat is. Kunst heeft namelijk een ''functie'' in ons leven. Elke kunstvorm stelt namelijk mensen in staat iets meer van de werkelijkheid waar te nemen, ons begrip van de werkelijkheid te vergroten, of er op een andere manier mee om te gaan. | <br/>Je kunt ook over kunst praten en nadenken op een heel andere manier. Kunst kan ook een bron van kennis zijn net als de wetenschap dat is. Kunst heeft namelijk een ''functie'' in ons leven. Elke kunstvorm stelt namelijk mensen in staat iets meer van de werkelijkheid waar te nemen, ons begrip van de werkelijkheid te vergroten, of er op een andere manier mee om te gaan. | ||
<br/>Kunst speelt ook een belangrijke rol in de menselijke communicatie. | <br/>Kunst speelt ook een belangrijke rol in de menselijke communicatie. | ||
==Wiskunde== | ==Wiskunde== | ||
Er is natuurlijk ook een heel andere benadering van de vloersculptuur mogelijk, namelijk een wiskundige. | Er is natuurlijk ook een heel andere benadering van de vloersculptuur mogelijk, namelijk een wiskundige. | ||
| Regel 76: | Regel 95: | ||
In de bijgaande tabel is van alle veelhoeken die deel uitmaken van de grondsculptuur de zijde '''z''' berekend van alle veelhoeken, uitgedrukt in de '''omschreven cirkel''' met straal '''R'''. | In de bijgaande tabel is van alle veelhoeken die deel uitmaken van de grondsculptuur de zijde '''z''' berekend van alle veelhoeken, uitgedrukt in de '''omschreven cirkel''' met straal '''R'''. | ||
<br/>Als de straal R van de omschreven cirkel bekend is, dan geldt voor de afmeting van zijde '''z''' : | <br/>Als de straal R van de omschreven cirkel bekend is, dan geldt voor de afmeting van zijde '''z''' : | ||
:* '''z = 2 R sin ( 180<sup> | :* '''z = 2 R sin ( 180<sup> 0</sup> '''/''' n''' ) , waarbij '''n''' het aantal hoeken '''α''' of zijden '''z''' is. | ||
Ook zijn de hoeken '''α''' en de som van de hoeken '''Σ''' in de tabel opgenomen. | Ook zijn de hoeken '''α''' en de som van de hoeken '''Σ''' in de tabel opgenomen. | ||
<br/>In de regelmatige vijfhoek hiernaast, zijn deze elementen aangegeven. | <br/>In de regelmatige vijfhoek hiernaast, zijn deze elementen aangegeven. | ||
| Regel 143: | Regel 162: | ||
|} | |} | ||
Opvallend is, dat bij elke veelhoek een stap van 180<sup> 0</sup> wordt gezet, waardoor de aanvankelijke 180<sup> 0</sup> van de driehoek uitkomt op 1800<sup> 0</sup> van de twaalfhoek. | Opvallend is, dat bij elke veelhoek een stap van 180<sup> 0</sup> wordt gezet, waardoor de aanvankelijke 180<sup> 0</sup> van de driehoek uitkomt op 1800<sup> 0</sup> van de twaalfhoek. | ||
===Priemgetallen=== | ===Priemgetallen=== | ||
De reeks veelhoeken bevat ook enkele '''priemgetallen''', namelijk de getallen '''3, 5, 7''' en '''11'''. Priemgetallen zijn getallen die alleen maar door zichzelf of door het getal '''1''' gedeeld kunnen worden. De overige getallen - dus '''4, 6, 8, 9''' en '''12''' - zijn geen priemgetallen, aangezien ze door de priemgetallen '''2''' of '''3''' gedeeld kunnen worden. | De reeks veelhoeken bevat ook enkele [[Priemgetallen|'''priemgetallen''']], namelijk de getallen '''3, 5, 7''' en '''11'''. | ||
<br/>Priemgetallen zijn getallen die alleen maar door zichzelf of door het getal '''1''' gedeeld kunnen worden. De overige getallen - dus '''4, 6, 8, 9''' en '''12''' - zijn geen priemgetallen, aangezien ze door de priemgetallen '''2''' of '''3''' gedeeld kunnen worden. | |||
<br/>Priemgetallen hebben een bijzondere plaats in de wiskunde en houden al eeuwen grote wiskundigen in de ban. | <br/>Priemgetallen hebben een bijzondere plaats in de wiskunde en houden al eeuwen grote wiskundigen in de ban. | ||
<br/>Uitgezonderd de '''driehoek''', zijn de veelhoeken met een priemgetal - dus de '''vijfhoek''', de '''zevenhoek''' en de '''elfhoek''' - bijzonder lastig te construeren en vragen om een bijzondere benadering. | <br/>Uitgezonderd de '''driehoek''', zijn de veelhoeken met een priemgetal - dus de '''vijfhoek''', de '''zevenhoek''' en de '''elfhoek''' - bijzonder lastig te construeren en vragen om een bijzondere benadering. | ||
| Regel 164: | Regel 185: | ||
De vloersculptuur begint met rijen '''driehoekige''' staven, en eindigt in een rij van bijna ''ronde'', '''twaalfhoekige''' staven. | De vloersculptuur begint met rijen '''driehoekige''' staven, en eindigt in een rij van bijna ''ronde'', '''twaalfhoekige''' staven. | ||
Naarmate het aantal zijden van de staven stijgt, wordt dus steeds meer de '''cirkel''' benaderd. | Naarmate het aantal zijden van de staven stijgt, wordt dus steeds meer de '''cirkel''' benaderd. | ||
<br/>De [[Rondom de cirkel ( 2 )|cirkel ]] blijkt van | <br/>De [[Rondom de cirkel ( 2 )|cirkel ]] blijkt van alle meetkundige figuren de figuur te zijn die de grootste | ||
'' | {{vbreuk|'''oppervlak|omtrek'''}} verhouding bezit, of anders gezegd: de cirkel bezit bij een gegeven oppervlak '''''( A )''''' van alle meetkundige figuren de kleinste omtrek '''''( O )'''''. | ||
<br/>Dit kan met eenvoudige berekeningen worden aangetoond, uitgaande van de formules die bij de ''oppervlakken'' en de ''omtrekken'' van de '''regelmatige veelhoeken''' horen. | <br/>Dit kan met eenvoudige berekeningen worden aangetoond, uitgaande van de formules die bij de ''oppervlakken'' en de ''omtrekken'' van de '''regelmatige veelhoeken''' horen. | ||
<br/>Om de verhouding tussen het oppervlak '''''A''''' en de omtrek ''''' O''''' in procenten te kunnen uitdrukken, worden de bij de figuren horende formules ''dimensieloos'' gemaakt, waarvoor enkele handelingen nodig zijn. Hierbij wordt uitgegaan van de formules die bij de cirkel horen, waarbij | <br/>Om de verhouding tussen het oppervlak '''''A''''' en de omtrek ''''' O''''' in procenten te kunnen uitdrukken, worden de bij de figuren horende formules ''dimensieloos'' gemaakt, waarvoor enkele handelingen nodig zijn. Hierbij wordt uitgegaan van de formules die bij de cirkel horen, waarbij | ||
| Regel 179: | Regel 200: | ||
De resultaten van de berekeningen zijn ondergebracht in bijgaande tabel. | De resultaten van de berekeningen zijn ondergebracht in bijgaande tabel. | ||
[[Afbeelding:Grafiek staven.jpg|500px|right]] | [[Afbeelding:Grafiek staven.jpg|500px|right]] | ||
{| | {| |- | ||
|- | |||
|- | |- | ||
|} | |} | ||
| Regel 187: | Regel 207: | ||
!4 π A/O<sup> 2</sup> · 100% | !4 π A/O<sup> 2</sup> · 100% | ||
|- | |- | ||
|1. Driehoek | |'''1. Driehoek''' | ||
|60,5 | |'''60,5''' | ||
|- | |- | ||
|2. Vierkant | |'''2. Vierkant''' | ||
|78,5 | |'''78,5 | ||
|- | |- | ||
|3. Vijfhoek | |'''3. Vijfhoek''' | ||
|86,5 | |'''86,5''' | ||
|- | |- | ||
|4. Zeshoek | |'''4. Zeshoek''' | ||
|90,7 | |'''90,7''' | ||
|- | |- | ||
|5. Zevenhoek | |'''5. Zevenhoek''' | ||
|93,2 | |'''93,2''' | ||
|- | |- | ||
|6. Achthoek | |'''6. Achthoek''' | ||
|94,8 | |'''94,8''' | ||
|- | |- | ||
|7. Negenhoek | |7. '''Negenhoek''' | ||
|95,9 | |'''95,9''' | ||
|- | |- | ||
|8. Tienhoek | |'''8. Tienhoek''' | ||
|96,7 | |'''96,7''' | ||
|- | |- | ||
|9. Elfhoek | |'''9. Elfhoek''' | ||
|97,3 | |'''97,3''' | ||
|- | |- | ||
|10. Twaalfhoek | |'''10. Twaalfhoek''' | ||
|97,7 | |'''97,7''' | ||
|- | |- | ||
| | |'''11. Cirkel''' | ||
|'''100''' | |||
<span style="font-size:100%;> | <span style="font-size:100%;> | ||
<font color = green> | <font color = green> | ||
|- | |||
| | |||
|} | |} | ||
<br/>Om nog een beter inzicht te krijgen in de verhouding tussen het oppervlak '''''A''''' en de omtrek '''''O''''' van de berekende veelhoeken, zijn de in de tabel genoemde resultaten weergegeven in bijgaande grafiek. | <br/>Om nog een beter inzicht te krijgen in de verhouding tussen het oppervlak '''''A''''' en de omtrek '''''O''''' van de berekende veelhoeken, zijn de in de tabel genoemde resultaten weergegeven in bijgaande grafiek. | ||
<br/>De nummers in de grafiek komen overeen met de nummers in de tabel. | <br/>De nummers in de grafiek komen overeen met de nummers in de tabel. | ||
==Nawoord== | ==Nawoord== | ||
Het blijkt, dat de vloersculptuur ''A Computer Which Will Solve Every Problem in the World'' voor de aandachtige toeschouwer een aantal bijzondere invalshoeken kan opleveren. | *Het blijkt, dat de vloersculptuur ''A Computer Which Will Solve Every Problem in the World'' voor de aandachtige toeschouwer een aantal bijzondere invalshoeken kan opleveren. | ||
:In dit essay is getracht enkele hiervan te belichten en te trachten samenhang te vinden tussen enkele disciplines.Het blijkt, dat de sculptuur zowel vanuit de '''Kunst''' als vanuit de '''Wiskunde''' kan worden bekeken, zonder dat dit tegenstrijdig behoeft te zijn; integendeel: beide disciplines vullen elkaar aan. De kunst wordt hier gesteund door de wiskunde. | |||
*''In [[Kunst en Wiskunde II]] gaat het over metalen staven en draden die op listige wijze in een kunstwerk zijn verwerkt.'' | |||
==Externe links== | ==Externe links== | ||
| Regel 245: | Regel 259: | ||
:: ''Wiskunde is een taal die net als proza en poëzie weet te bekoren met mooie zinnen!'' | :: ''Wiskunde is een taal die net als proza en poëzie weet te bekoren met mooie zinnen!'' | ||
:* Stichting ''Ars et Mathesis'' ( Kunst en Wiskunde ) te Amsterdam. Deze stichting heeft tot doel de belangstelling te bevorderen voor Kunst die zijn inspiratie vindt in de Wiskunde. | :* Stichting ''Ars et Mathesis'' ( Kunst en Wiskunde ) te Amsterdam. Deze stichting heeft tot doel de belangstelling te bevorderen voor Kunst die zijn inspiratie vindt in de Wiskunde. | ||
[[Categorie:Wiskunde]] | |||
[[Categorie:Kunst]] | |||
[[en:Essay:Kunst_en_Wiskunde_I]] | |||
Huidige versie van 7 sep 2017 om 15:36

Wat onderga je, als je als bezoeker in een museum op de vloer een groot aantal blinkende staven ziet liggen?
De een zal er even naar kijken, er geen raad mee weten en verder lopen. De ander zal wat meer belangstelling tonen en op onderzoek uitgaan.
Het is in ieder geval zó, dat deze uitstalling de meeste mensen niet geheel onverschillig laat, en dat minstens je nieuwsgierigheid wordt gewekt. Misschien dringt zelfs de achterliggende gedachte aan je op, dat hier iets bijzonders aan de hand is.
Vloersculptuur

Het werk op de afbeelding – een indrukwekkend vloersculptuur - is door de Amerikaan Walter De Maria (1935-2013) in 1984 gemaakt in opdracht van Museum Boymans – Van Beuningen in Rotterdam. De naam die de kunstenaar aan dit werk meegaf luidt: A Computer Which Will Solve Every Problem in the World (Een computer die elk probleem in de wereld zal oplossen).
Het werk bestaat uit 75 gepolijste roestvast stalen staven, die in rijen op de vloer zijn neergelegd en die elk precies een meter lang zijn.
Bij een eerste verkenning valt je onmiddellijk op, dat de heldere en gelijkmatige opbouw van de vloersculptuur bij iedere verandering van standpunt een nieuw beeld oplevert.
In de rangschikking op de vloer blijkt een strikte ordening te heersen, die
zich pas na enig zoeken en nadenken prijsgeeft. Het blijkt, dat - beginnend met een rij van drie driehoekige staven – de sculptuur eindigt in een rij van twaalf - bijna ronde - twaalfhoekige staven. Alle rijen staven blijken dus opgebouwd te zijn uit steeds oplopende regelmatige
veelhoeken 1).
In deze rangschikking liggen er dus tien rijen in een bijbehorend patroon, waarbij dus - naarmate de rijen opschuiven – het aantal facetten van de staven stijgt, waardoor steeds meer de vorm van een cirkel wordt benaderd.
De lengte van een meter is aanwezig in de gehele opstelling: ook de evenwijdige rijen bevinden zich steeds op een meter afstand van elkaar.
1) Regelmatige veelhoeken zijn tweedimensionale meetkundige figuren, bestaande uit een eindig aantal lijnstukken ( zijden ) die alle dezelfde lengte hebben, en waarvan alle hoeken even groot zijn.
Herhaling
De kracht van het kunstwerk zit voor een deel in de herhaling, met steeds een subtiele toevoeging. De herhaling heeft hier betrekking op:
|
|
- dezelfde lengte van de staven
- het gelijke oppervlak van alle staven
- het gelijke gewicht van alle staven
- de uitbreiding per rij van het aantal staven
- de toevoeging per rij van een zijde van de veelhoek
- dezelfde onderlinge afstanden tussen de rijen
Vanuit een geheel andere kunstvorm - de muziek - kan van dit sculptuur, wat betreft herhaling, een vergelijking worden gemaakt met de Boléro van Maurice Ravel, of met Le Bœuf sur le toit van Darius Milhaud.
- De Boléro bestaat uit twee afwisselende thema's, elk van zestien maten, die telkens door andere instrumenten worden gespeeld. Beide maten worden 9 keer letterlijk herhaald. Na twee inleidende maten door de kleine trom wordt het eerste thema ingezet door een enkele fluit, waarna langzamerhand het gehele orkest gaat meedoen.
In 1919 keerde Darius Milhaud - na een langdurig verblijf in Brazilië - terug naar Parijs en schreef zijn zeer bekend geworden Le Bœuf sur le toit ( De os op het dak ). Deze titel is afkomstig van een oud volkswijsje, dat Milhaud tijdens het carnaval in Rio de Janeiro hoorde.
- De compositie Le Bœuf sur le toit is geen getrouwe weergave van het volkswijsje, maar is meer een opeenvolging van scènes, geïnspireerd door de oorspronkelijk melodie, en in de trant van de Braziliaanse volksmuziek. In het muziekstuk komt maar liefst 14 keer het hoofdthema terug in de vorm van een rondo, maar steeds in een andere toonzetting.
A Computer Which Will Solve Every Problem in the World
De vloersculptuur werd door Walter De Maria ontworpen in 1984, voordat computers uitgroeiden tot de allesomvattende apparaten die ze tegenwoordig zijn.
Walter De Maria was er zich er natuurlijk van bewust, dat computers in staat zijn nogal wat economische en technische problemen op te lossen, maar dat er zich in het leven andere opgaven en problemen voordoen die buiten het bereik van computers vallen en dus hierdoor ook niet kunnen worden opgelost.
|
|
De badinerende titel: A Computer Which Will Solve Every Problem in the World die hij aan het kunstwerk meegaf, geeft dus aan, dat voor hem de antwoorden op problemen niet altijd op een logische of rationele manier kunnen worden benaderd, maar dat er ook andere wegen zijn als een verhoogd bewustzijn via waarneming of intuïtie, zeker als het om de kunst gaat.
In de poëzie kom je hetzelfde tegen, vooral in de moderne poëzie. Sommige teksten zijn namelijk op het eerste gezicht niet altijd even logisch, maar het op je laten inwerken en de atmosfeer ervan proeven is dikwijls al voldoende. De Vlaamse dichter Paul van Ostaijen (1896 -1928 ) is hier een duidelijk voorbeeld van. In zijn gedicht VORST mis je de logica, maar proef je het gevoel.
- VORST
Is vorst
- breken scherp en helder stenen rijen
- wegen scheuren
Schel schelt de schel
- van de trem in duizelruimte
- hoge hoepel
- staalhemel staalhelm
Naar klare spanbanen strammen stappen
- laarzen slaan de straat tot luide ruimte
Is vorst
- breken stenen scherp
- staan laarzen klaar
- schellen de schellen schel
- helder
- helder
- helder
- helder
duizelruimte luidt
Ook in de schilderkunst kom je op hetzelfde vlak uit. De Nederlandse schilders als Piet Mondriaan en Theo van Doesburg hielden zich bezig met puur geometrische figuren waarvan alle vormen zijn teruggebracht tot het uiterste met een beperkt kleurgebruik. Ook schilders als Kassimir Malevich en El Lissitzky waren op soortgelijke wijze bezig.
Is het kunst?
De vloersculptuur van Walter De Maria wordt gerekend tot het Minimalisme.
Het minimalisme in de beeldende kunst heeft zich - in de jaren zestig - vooral in Amerika sterk ontwikkeld. De naam van deze trend geeft goed weer wat ermee wordt bedoeld, namelijk dat de kunst tot zijn essentie is teruggebracht, volledig abstract, objectief en vrij van alle verfraaiingen en versierselen. De minimalistische sculpturen moeten het geheel hebben van de directe ervaring die de toeschouwer ondergaat.
Ook hier dringt zich natuurlijk de vraag op:
- Maar is dit kunst?
Deze vraag is – zoals dit al heel lang het geval is – niet eenduidig te beantwoorden, en een eventueel antwoord zal dus nooit voor iedereen geldig zijn.
Dat kunst iets bijzonders inhoudt, lijkt niet ter discussie te staan. Veel mensen hebben grote waardering voor de kunst, ook voor de moderne kunst die voorop loopt in het onderzoeken en vergroten van ons bewustzijn, en die soms provocerend kan zijn.
Er is een heldere uitspraak van de Amerikaanse kunstenaar Robert Irwin, die aangeeft, dat:
- Kunst een continu onderzoek is van ons op waarneming gebaseerde bewustzijn, en is een continue verruiming van de ons omringende wereld.
Deze uitspraak lijkt bijna geheel van toepassing op het sculptuur van Walter De Maria. We onderzoeken en vergroten ons bewustzijn bij het waarnemen en laten inwerken van de sculptuur op je en het ontdekken van patronen in de opstelling.
Je kunt ook over kunst praten en nadenken op een heel andere manier. Kunst kan ook een bron van kennis zijn net als de wetenschap dat is. Kunst heeft namelijk een functie in ons leven. Elke kunstvorm stelt namelijk mensen in staat iets meer van de werkelijkheid waar te nemen, ons begrip van de werkelijkheid te vergroten, of er op een andere manier mee om te gaan.
Kunst speelt ook een belangrijke rol in de menselijke communicatie.
Wiskunde
Er is natuurlijk ook een heel andere benadering van de vloersculptuur mogelijk, namelijk een wiskundige.
Het zal duidelijk zijn, dat de voorgaande beschouwingen niet uitsluiten, dat bij de opzet van het project berekeningen nodig zijn geweest. Het is dus vanzelfsprekend, dat - als er staven met oplopende regelmatige veelhoeken worden ontworpen en vervaardigd - er enige wiskunde aan te pas moet zijn gekomen.
Zijden van de veelhoeken
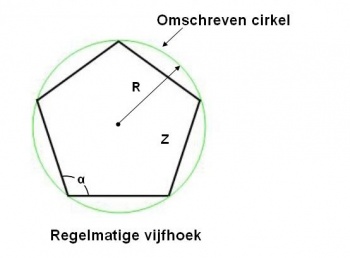
In de bijgaande tabel is van alle veelhoeken die deel uitmaken van de grondsculptuur de zijde z berekend van alle veelhoeken, uitgedrukt in de omschreven cirkel met straal R.
Als de straal R van de omschreven cirkel bekend is, dan geldt voor de afmeting van zijde z :
- z = 2 R sin ( 180 0 / n ) , waarbij n het aantal hoeken α of zijden z is.
Ook zijn de hoeken α en de som van de hoeken Σ in de tabel opgenomen.
In de regelmatige vijfhoek hiernaast, zijn deze elementen aangegeven.
Tabel van de toegepaste regelmatige veelhoeken
| Naam van
de veelhoek |
Hoek van
de regelmatige
|
Som van
de hoeken ( Σ ) |
zijde z |
|---|---|---|---|
| Driehoek | 60 0 | 180 0 | 1,73205 • R |
| Vierkant | 90 0 | 360 0 | 1,41442 • R |
| Vijfhoek | 108 0 | 540 0 | 1,17557 • R |
| Zeshoek | 120 0 | 720 0 | 1 • R |
| Zevenhoek | 128,5714 0 | 900 0 | 0,86776 • R |
| Achthoek | 135 0 | 1080 0 | 0,76535 • R |
| Negenhoek | 140 0 | 1260 0 | 0,68404 • R |
| Tienhoek | 144 0 | 1440 0 | 0,61803 • R |
| Elfhoek | 147,2727 0 | 1620 0 | 0,56347 • R |
| Twaalfhoek | 150 0 | 1800 0 | 0,51764 • R |
Opvallend is, dat bij elke veelhoek een stap van 180 0 wordt gezet, waardoor de aanvankelijke 180 0 van de driehoek uitkomt op 1800 0 van de twaalfhoek.
Priemgetallen
De reeks veelhoeken bevat ook enkele priemgetallen, namelijk de getallen 3, 5, 7 en 11.
Priemgetallen zijn getallen die alleen maar door zichzelf of door het getal 1 gedeeld kunnen worden. De overige getallen - dus 4, 6, 8, 9 en 12 - zijn geen priemgetallen, aangezien ze door de priemgetallen 2 of 3 gedeeld kunnen worden.
Priemgetallen hebben een bijzondere plaats in de wiskunde en houden al eeuwen grote wiskundigen in de ban.
Uitgezonderd de driehoek, zijn de veelhoeken met een priemgetal - dus de vijfhoek, de zevenhoek en de elfhoek - bijzonder lastig te construeren en vragen om een bijzondere benadering.
Kwadraten
Er blijkt ook nog een verdere samenhang en herhaling tussen de rijen staven te bestaan.
Zoals aangegeven, begint de sculptuur met een rij van drie driehoekige staven, en eindigt dit in een rij van twaalf twaalfhoekige staven. Elke rij bevat dus totaal
- n • n = n 2
hoeken of zijden van de veelhoek, wat dus het kwadraat van het aantal hoeken of zijden is.
Het blijkt, dat bij een reeks kwadraten, tussen twee opvolgende kwadraten een samenhang bestaat. Tussen twee opvolgende kwadraten is namelijk de volgende betrekking aanwezig:
- n 2 = ( n – 1 ) 2 + ( n – 1 ) + n
Voor bijvoorbeeld de 4 e rij in betrekking tot de 3 e rij geldt dus:
- 4 2 = ( 4 – 1 ) 2 + ( 4 – 1 ) + 4 = 9 + 3 + 4 = 16
En voor de laatste rij geldt dan:
- 12 2 = ( 12 – 1 ) 2 + ( 12 – 1 ) + 12 = 121 + 11 + 12 = 144
In totaal zijn dus 3 2 + 4 2 + 5 2 + 6 2 + 7 2 + 8 2 + 9 2 + 10 2 + 11 2 + 12 2 = 645 vlakken z aanwezig.
Verhouding tussen oppervlak en omtrek van de staven
De vloersculptuur begint met rijen driehoekige staven, en eindigt in een rij van bijna ronde, twaalfhoekige staven.
Naarmate het aantal zijden van de staven stijgt, wordt dus steeds meer de cirkel benaderd.
De cirkel blijkt van alle meetkundige figuren de figuur te zijn die de grootste
oppervlak omtrek verhouding bezit, of anders gezegd: de cirkel bezit bij een gegeven oppervlak ( A ) van alle meetkundige figuren de kleinste omtrek ( O ).
Dit kan met eenvoudige berekeningen worden aangetoond, uitgaande van de formules die bij de oppervlakken en de omtrekken van de regelmatige veelhoeken horen.
Om de verhouding tussen het oppervlak A en de omtrek O in procenten te kunnen uitdrukken, worden de bij de figuren horende formules dimensieloos gemaakt, waarvoor enkele handelingen nodig zijn. Hierbij wordt uitgegaan van de formules die bij de cirkel horen, waarbij
het oppervlak A van een cirkel is:
- Acirkel = π r 2
en de omtrek O van een cirkel is:
- Ocirkel = 2 π r
De dimensie van de straal r is de lengte l, zodat dus r 2 de dimensie l 2 heeft.
Door nu het oppervlak A te delen door de omtrek O in het kwadraat, vallen de dimensies van de lengte l tegen elkaar weg. Verder is er door invoering van de getalwaarden 4π en 100% voor gezorgd, dat de verhouding tussen oppervlak en omtrek bij de cirkel op 100% uitkomt.
Voor alle regelmatige veelhoeken
- uitgezonderd de cirkel - geldt nu:
- 4 π A/O 2 · 100% = < 100%
De resultaten van de berekeningen zijn ondergebracht in bijgaande tabel.
| Regelmatige veelhoek | 4 π A/O 2 · 100% |
|---|---|
| 1. Driehoek | 60,5 |
| 2. Vierkant | 78,5 |
| 3. Vijfhoek | 86,5 |
| 4. Zeshoek | 90,7 |
| 5. Zevenhoek | 93,2 |
| 6. Achthoek | 94,8 |
| 7. Negenhoek | 95,9 |
| 8. Tienhoek | 96,7 |
| 9. Elfhoek | 97,3 |
| 10. Twaalfhoek | 97,7 |
| 11. Cirkel | 100
|
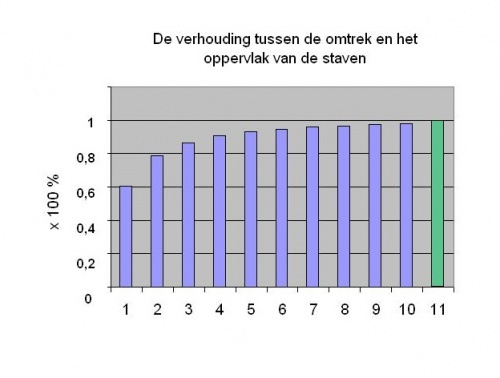
Om nog een beter inzicht te krijgen in de verhouding tussen het oppervlak A en de omtrek O van de berekende veelhoeken, zijn de in de tabel genoemde resultaten weergegeven in bijgaande grafiek.
De nummers in de grafiek komen overeen met de nummers in de tabel.
Nawoord
- Het blijkt, dat de vloersculptuur A Computer Which Will Solve Every Problem in the World voor de aandachtige toeschouwer een aantal bijzondere invalshoeken kan opleveren.
- In dit essay is getracht enkele hiervan te belichten en te trachten samenhang te vinden tussen enkele disciplines.Het blijkt, dat de sculptuur zowel vanuit de Kunst als vanuit de Wiskunde kan worden bekeken, zonder dat dit tegenstrijdig behoeft te zijn; integendeel: beide disciplines vullen elkaar aan. De kunst wordt hier gesteund door de wiskunde.
- In Kunst en Wiskunde II gaat het over metalen staven en draden die op listige wijze in een kunstwerk zijn verwerkt.
Externe links
- Cynthia Freeland: But Is It Art? An Introduction to Art Theory, Oxford University Press
- Nederlandse vertaling: Maar is dit kunst? Een inleiding in de kunsttheorie, Uitgeverij Prometheus en Ruth Visser.
- De vloersculptuur van Walter De Maria was van 28 mei t/m 18 september 2011 te zien in De Pont in Tilburg, www.depont.nl
- Op de Universiteit van Twente stond in april 2011 de schoonheid van wiskunde centraal in een congres. Bij de opening van dit congres, werd deze zin gelanceerd:
- Wiskunde is een taal die net als proza en poëzie weet te bekoren met mooie zinnen!
- Stichting Ars et Mathesis ( Kunst en Wiskunde ) te Amsterdam. Deze stichting heeft tot doel de belangstelling te bevorderen voor Kunst die zijn inspiratie vindt in de Wiskunde.

