Parallellepipedum: verschil tussen versies

Huidige versie van 9 mrt 2015 om 02:06

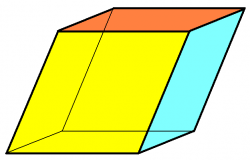
Een parallellepipedum is een veelvlak met zes parallellogrammen als zijvlak, 8 hoekpunten en 12 ribben, waarvan alle overstaande vlakken evenwijdig zijn en twee-aan-twee, gezien van de buitenkant, elkaars spiegelbeeld. Drie equivalente definities van een parallellepipedum zijn

een veelvlak met zes zijdes (hexahedron), die alle zes een parallellogram zijn,
een hexahedron met drie paren van parallelle zijdes.
een prisma, waarvan het grondvlak een parallellogram is,

De balk (zes rechthoekige zijdes), kubus (zes vierkante zijdes), en de rhombohedron (zes ruitvormige zijdes) zijn alle specifieke gevallen van een 'parallellepipedum'.

Definitie

In drie dimensies is een parallellepipedum een prisma waarvan alle zijden parallellogrammen zijn. Als A, B en C de basisvectoren zijn van het parallellepipedum, dan heeft de figuur het volume:

V = |A · (B × C)|

  = |C · (A × B)|

  = |B · (C × A)|

of, als we de vectoren A, B, C definiëren:

A = (a₁, a2, a₃)

B = (b₁, b₂, b₃)

C = (c₁, c₂, c₃)

|A · (B · C) | = | a₁ b₁ c₁ a₂ & b₂ & c₂ a₃ & b₃ & c₃

         = a₁

b₂ & c₂

b₃ & c₃

– a₂

b₁ & c₁

b₃ & c₃ + a₃

b₁ & c₁

b₂ & c₂

         = a₁ · (b₂ · c₃ – b₃ · c₂) – a₂ · (b₁ · c₃ – b₃ · c₁) + a₃ · (b₁ · c₂ – b₂ · c₁)
         = a₁ · b₂ · c₃ – a₁ · b₃ · c₂ – a₂ · b₁ · c₃ + a₂ · b₃ · c₁ + a₃ · b₁ · c₂ – a₃ · b₂ c₁

Vrije mediabestanden over Parallelepiped op Wikimedia Commons

@@ Regel 12: / Regel 12: @@
 In drie dimensies is een parallellepipedum een prisma waarvan alle zijden parallellogrammen zijn.
 Als A, B en C de basisvectoren zijn van het parallellepipedum, dan heeft de figuur het volume:
+<font face="Times New Roman">
-  V = |A.(BxC)|
+  V = |A · (B × C)|
-    = |C.(AxB)|
+    = |C · (A × B)|
-    = |B.(CxA)|
+    = |B · (C × A)|
+</font>
+of, als we de vectoren A, B, C definiëren:
+<font face="Times New Roman">A = (a<sub>1</sub>, a2, a<sub>3</sub>)
+B = (b<sub>1</sub>, b<sub>2</sub>, b<sub>3</sub>)
-of<!-- nog (?)-->, als we de vectoren A, B, C definiëren:
+C = (c<sub>1</sub>, c<sub>2</sub>, c<sub>3</sub>)</font>
-A(a1,a2,a3)
-B(b1,b2,b3)
+|A · (B · C) | = |
+a<sub>1</sub>&nbsp;&nbsp;b<sub>1</sub>&nbsp;&nbsp;c<sub>1</sub>
+a<sub>2</sub> & b<sub>2</sub> & c<sub>2</sub>
+a<sub>3</sub> & b<sub>3</sub> & c<sub>3</sub>
-C(c1,c2,c3)
+          = a<sub>1</sub>
-<math>|A.(B \times C) | = | \begin{vmatrix}
+ b<sub>2</sub> & c<sub>2</sub>
-a1 & b1 & c1 \\
-a2 & b2 & c2 \\
-a3 & b3 & c3 \end{vmatrix} |
-          = a1
+  b<sub>3</sub> & c<sub>3</sub>
-\begin{vmatrix}
+–
- b2 & c2 \\
+a<sub>2</sub>
-  b3 & c3 \end{vmatrix}
--
+b<sub>1</sub> & c<sub>1</sub>
-a2
-\begin{vmatrix}
+b<sub>3</sub> & c<sub>3</sub>
- b1 & c1 \\
- b3 & c3 \end{vmatrix}
 +
-a3
+a<sub>3</sub>
-\begin{vmatrix}
-b1 & c1 \\
+b<sub>1</sub> & c<sub>1</sub>
-b2 & c2 \end{vmatrix}
-           = a1.(b2.c3 - b3.c2) - a2.(b1.c3 - b3.c1) + a3.(b1.c2 - b2.c1)
+b<sub>2</sub> & c<sub>2</sub>
-           = a1.b2.c3 - a1.b3.c2 - a2.b1.c3 + a2.b3.c1 + a3.b1.c2 - a3.b2.c1</math>
+           = a<sub>1</sub> · (b<sub>2</sub> · c<sub>3</sub> – b<sub>3</sub> · c<sub>2</sub>) – a<sub>2</sub> · (b<sub>1</sub> · c<sub>3</sub> – b<sub>3</sub> · c<sub>1</sub>) + a<sub>3</sub> · (b<sub>1</sub> · c<sub>2</sub> – b<sub>2</sub> · c<sub>1</sub>)
+           = a<sub>1</sub> · b<sub>2</sub> · c<sub>3</sub> – a<sub>1</sub> · b<sub>3</sub> · c<sub>2</sub> – a<sub>2</sub> · b<sub>1</sub> · c<sub>3</sub> + a<sub>2</sub> · b<sub>3</sub> · c<sub>1</sub> + a<sub>3</sub> · b<sub>1</sub> · c<sub>2</sub> – a<sub>3</sub> · b<sub>2</sub> c<sub>1</sub>
 {{commons|Parallelepiped}}
 [[Categorie:Ruimtelijke figuur]]

Parallellepipedum: verschil tussen versies

Huidige versie van 9 mrt 2015 om 02:06

Definitie

Navigatiemenu

Zoeken