Gebruiker:Franciscus/kladblok

Deelonderwerp

Deze pagina gebruik ik om nieuwe artikelen even op te bergen en te bewerken, vóórdat ik ze als bijdrage op Wikisage zet. Ook kan ik hier enkele geheugensteuntjes kwijt.
Franciscus 4 feb 2009 14:55 (UTC)

Priemgetallen

Priemgetallen zijn tamelijk mysterieus van aard. Ondanks dat priemgetallen al sinds de oudheid worden bestudeerd, zijn er nog veel onbeantwoorde vragen. Sinds eeuwen wordt bijvoorbeeld door wiskundigen gezocht naar enige regelmaat in de oneindige reeks priemgetallen. Voor een deel zijn hierin inmiddels al wat successen geboekt, maar nog steeds in men zoekende. Maar er zijn nog wel meer belangrijke vragen bij priemgetallen die om een oplossing vragen. Men is druk doende ook daar achter te komen.

Priemgetallen zijn tamelijk mysterieus van aard.

• Wat is eigenlijk een priemgetal?

Een priemgetal is een natuurlijk getal, dat slechts twee quotiënten heeft:
1 én het getal zelf.
Natuurlijke getallen zijn alle gehele getallen > 0 : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, enz.
Een priemgetal is bijvoorbeeld het getal 17 , want het is alleen deelbaar door 1 én door 17. Het getal 18 is géén priemgetal, want het is deelbaar door 1 én door 18 , dat opgebouwd is uit de priemgetallen 2 en 3,
namelijk: 2 • 3 • 3 = 2 • 3 ².

Reeks priemgetallen

De reeks priemgetallen tot 100 bestaat uit:

• 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97,

( Het getal 91 lijkt op het eerste gezicht een priemgetal te zijn, maar is gewoon het product van 7 en 13! )

Tot het getal 100, blijken er dus 25 priemgetallen aanwezig te zijn.
In 300 v.Chr. bewees Euclides al, dat er een oneindig aantal priemgetallen is. Van alle natuurlijke getallen is ongeveer 18% een priemgetal.. Dat betekent dat het grootste priemgetal niet bestaat omdat er altijd nog een groter priemgetal is.

Gehele getallen

Priemgetallen bezitten naast hun primaire eigenschap nog een andere bijzondere eigenschap. Het blijkt namelijk, dat alle gehele getallen - die geen priemgetallen zijn - bestaan bij de gratie van met elkaar vermenigvuldigde priemgetallen. Priemgetallen zijn dus de basis van alle gehele getallen.
Neem als voorbeeld het getal 84. Dit getal kan worden ontleed in:

• 2 • 2 • 3 • 7 = 2² • 3 • 7

Of neem het getal 51. Dit lijkt heel even op een priemgetal, maar blijkt het quotiënt te zijn van 3 en 17.

Orde in de priemgetallen

Priemgetallen blijken niet zo willekeurig te zijn als men eerder had aangenomen. Er blijkt wel degelijk een patroon aanwezig te zijn. Vastgesteld is namelijk, dat een priemgetal dat op 1 eindigt tussen het getal 2 en 100 een aantal keren terugkeert. Eenzelfde patroon blijkt voor priemgetallen eindigend op 3, 7 en 9 te gelden. Ook die getallen blijken een aantal malen terug te keren. Deze 'wetmatigheid' levert het volgende beeld op:

Priemgetallen blijken niet zo willekeurig te zijn als men eerder had aangenomen.

• voor het getal 1 gelden de priemgetallen: 11, 31, 41, 61 en 71
• voor het getal 3 gelden de priemgetallen: 3, 13, 23, 43, 53, 73 en 83
• voor het getal 7 gelden de priemgetallen: 7, 17, 37, 47, 67 en 97
• voor het getal 9 gelden de priemgetallen: 19, 29, 59, 79 en 89

Ondanks dat het patroon minder sterk wordt bij hogere priemgetallen dan 1, 3, 7 en 9, is ook bij getallen >100 een zekere wetmatigheid aanwezig.
Wetenschappers beschouwen de opeenvolgende reeks priemgetallen als pseudowillekeurig aangezien er niet direct een duidelijke structuur aan te wijzen is.

Priemtweelingen

Priemtweelingen zijn paren van priemgetallen die dichtbij elkaar staan met slechts 2 cijfers verschil. Dat betekent, dat er tussen die twee getallen een even getal ligt.
Meestal schrijft men de priemtweelingen in de vorm: p en p+2. Voorbeelden hiervan zijn de priemgetallen 3 en 5, 5 en 7, en 17 en 19. In de bijgaande tabel zijn de priemtweelingen tot 200 opgenomen.

Priemtweelingen tot 200
3 en 5
5 en 7
17 en 19
29 en 31
41 en 43
59 en 61
71 en 73
101 en 103
107 en 109
149 en 151
179 en 181
191 en 193
197 en 199

De vraag is of er oneindig veel van deze tweelingen bestaan of dat de reeks eindig is. Hier wordt nog onderzoek naar gedaan.

Grote priemgetallen

De wetenschap is zo gefascineerd door priemgetallen dat er speciale computerprogramma’s geschreven zijn die zoeken naar steeds grotere priemgetallen. Het gaat om een zogenoemd Mersennepriemgetal. Een Mersennepriemgetal is een positief geheel getal dat precies 1 kleiner is dan een macht van twee. De priemgetallen die met momenteel gevonden worden, zijn allemaal Mersennegetallen (naar de Frans monnik en wiskundige Marin Mersenne). Deze getallen hebben de vorm: 2 ^p-1, waarbij p een priemgetal is, en dus oneven, bijvoorbeeld: 2³ – 1 = 7. Deze methode wordt momenteel als de meest efficiënte methode beschouwd om nieuwe priemgetallen te vinden.
Een eenvoudig voorbeeld van hoe een priemgetal kan worden herleid tot de bron is het volgende. Neem als voorbeeld het priemgetal 8191. De herkomst hiervan kan worden gevonden, door er eerst 1 bij op te tellen en te onderzoeken, of de algemene regel: 2 ^p-1 hier van toepassing is. Dit kan op een eenvoudige manier, door met de regels van de logaritmen te werken, aldus:

Bij dit betrekkelijk eenvoudige voorbeeld is het vinden van het priemgetal nog goed uitvoerbaar. Anders wordt het, bij de ontdekking van steeds groter wordende priemgetallen.
In 2002 was het grootste, bekende priemgetal 2^13.4666.917 - 1, een getal met 4.053.946 cijfers achter de komma. Helemaal uitgeschreven zou het ongeveer 20 km lang zijn. In 2013 werd opnieuw een grootste priemgetal geïntroduceerd, namelijk: 2^57.885.161 - 1, dat 17.425.170 decimalen bevat.
Heel snel daarna - namelijk in 2016 - werd er alweer een nieuw priemgetal gepubliceerd. Dit nieuwe, grootste priemgetal, namelijk: 2^74.207.281 - 1, telt 22.338.618 cijfers en is daarmee bijna 5 miljoen getallen groter dan de vorige recordhouder!
Dit nieuwste priemgetal is ontdekt door Curtis Cooper die deelnam aan het GIMPS {Great Internet Mersenne Prime Search).
Berekeningen die dit resultaat opleveren, kunnen alleen tot stand worden gebracht door de rekencapaciteit van een groot aantal computers te benutten.

Toepassing van priemgetallen

Hoewel priemgetallen mysterieus en wonderlijk aandoen, zijn ze van groot belang. Lange tijd dachten wiskundigen dat de getallen tot de zuivere wiskunde behoorden en dat er dus geen praktische toepassingen voor bestonden buiten de wiskunde. Veel van de huidige bank- en internetcodes maken er gebruik van. Twee priemgetallen met elkaar vermenigvuldigen om een uniek product te krijgen is dus eenvoudig, maar terugredeneren is zo lastig dat het een goede beveiligingsmethode is voor onder andere bankoverschrijvingen en codering van geheime berichten.
Neem als voorbeeld het getal 1219. Als getracht wordt het getal te delen door getallen onder de 10, dan lukt dit al niet. Ook met getallen onder de 20 gaat dit niet. Pas als men is aangeland bij het priemgetal 23, ontstaat er een deling, waarbij het priemgetal 53 de andere component blijkt te zijn. Het zal duidelijk zijn, dat naarmate het gekozen getal beduidend groter is, de berekening zonder hulpmiddelen niet zal lukken en dat het bijna ondoenlijk is het getal terug te brengen tot zijn elementaire factoren. Het omgaan met priemgetallen is dus geen wiskundig tijdverdrijf voor enkele specialisten, maar heeft wel degelijk een functie in het dagelijks leven.

Verdere ontwikkelingen

Wat weten we nog niet over priemgetallen?
Een bekend voorbeeld is het Vermoeden van Goldbach ²⁾. In dat Vermoeden wordt gesteld, dat elk even getal >2 geschreven kan worden als de som van twee priemgetallen. Dit klinkt eenvoudig, maar bewijzen, dat dit voor alle even getallen geldt blijkt lastig.
Een ander raadsel vormen de al eerder genoemde priemtweelingen. De vraag is of er oneindig veel van deze tweelingen bestaan of dat de reeks eindig is. Er wordt bijvoorbeeld nog onderzocht of er oneindig veel priemgetallen p bestaan waarvoor geldt, dat p + 2 eveneens een priemgetal is.
Een redelijk groot priemgetal is bijvoorbeeld p = 9719. Het blijkt, dat ook bij dit betrekkelijk grote getal nog steeds een priemtweeling aanwezig is in de vorm: p + 2= 9721. {{Bron|bronvermelding=

Dit is echter niet het enige vraagstuk over de eindigheid van bepaalde priemgetallen.

Een streamer bevat een korte tekst van twee of drie regels.

In sommige steden was men al zover, dat er een soort standaard werd aangehouden.

"Heeft men een goed boek uitgelezen, dan is het alsof men van een goede vriend afscheid neemt."

Priemgetallen blijken niet zo willekeurig te zijn als men eerder had aangenomen.

In het Engels zijn dit dan ook ‘quotes’ of ‘quotation marks’. Het is dus puur een vertaling uit het Engels en ze zijn dus hetzelfde, dan wel een synoniem van elkaar.

Een quote kan een synoniem van citaat zijn. als voorbeeld of illustratie aangehaalde uitspraak van iemand Quote’ is het Engelse woord voor ‘beurskoers’ maar ook voor ’ uitspraak/ citaat’. De uitspraak van iemand die aangehaald wordt uit een tekst, zal dan ook altijd tussen aanhalingstekens staan. (’) ("). In het Engels zijn dit dan ook ‘quotes’ of ‘quotation marks’. Het is dus puur een vertaling uit het Engels en ze zijn dus hetzelfde, dan wel een synoniem van elkaar. Heeft men een goed boek uitgelezen, dan is het alsof men van een goede vriend afscheid neemt. Voltaire

Er is een vuistregel, die aangeeft, dat om de 400 woorden de tekst gelardeerd kan worden met een streamer. Een streamer is een citaat uit een artikel, meestal een uitspraak, gezet tussen de tekst of in de marge. Een streamer moet Een streamer is een korte tekst van ongeveer vijf tot vijftien woorden. Hiervoor wordt als regel een opvallende zin uit de basistekst van het artikel gekozen. Het woord Streamer is een krantenjargon.
Bij een streamer plaats wordt meestal een extra groot lettertype gekozen, zodat deze goed opvalt.
Een streamer heeft als functie om de lezer nieuwsgierig te maken, om hem aan te zetten om het hele artikel te gaan lezen. Daarom worden hier opvallende citaten of bijzondere zinnen voor gebruikt. Als streamer neemt men een zin die aan het artikel ontleend is. Als er geen interessante streamer te vinden is in 400 woorden tekst, kan deze tekst gevoeglijk worden weggelaten.

maar krijgen geen punt aan het einde,. Soms bestaat een streamer uit twee zinnen: in dat geval krijgt de eerste zin wel een punt. Streamers kunnen een conclusie bevatten, of een 'quote', die we weergeven tussen enkel Engels. Die quote moet nagenoeg letterlijk overeenstemmen met de tekst: we moeten een quote tussen aanhalingstekens niet kortwieken of stroomlijnen. Zowel voor de kop als voor de streamer geldt dat we staande uitdrukkingen niet inkorten.
Een streamer is een citaat uit een artikel of een verhandeling , de nieuwsgierigheid prikkelt. Het mag gerust meer dan één streamer zijn. een prikkelende zin als zogeheten streamer hier en daar opgelicht in de tekst, en af en toe een opsomming.
Streamers worden gebruikt en de lezer te prikkelen om de tekst te gaan lezen. Elke streamer bevat 10 à 12 woorden. De opmaak zal cursief , groter lettertype en gecentreerde tekst zijn. Streamer Dit is een lay-out-technische term: een kop of tussenkop die enkele kolommen of de volledige breedte van de pagina bestrijkt.

Op een gegeven moment stelt hij vast, dat het een verloren zaak is.

Een streamer bevat een zeer korte tekst van twee of drie regels.

• Het schrijven van de Magister Ludi aan de Pedagogische Dienst

|} .

.....dat hij al tekenen waarneemt, dat in de nabije toekomst Het Kralenspel als eerste verloren zal gaan.

.....dat hij al tekenen waarneemt, dat in de nabije toekomst Het Kralenspel als eerste verloren zal gaan.

{{Overline| (12)}} om ergens een lijntje boven te trekken

{{Overline|24}}

12
24
12
--
24

Breuken

a ^b⁄_c: a b/c (geheel getal, teller en noemer) ^a⁄_b: a/b (teller en noemer) ¹⁄_a: 1/a (alleen noemer)

12
--
24

{{Overline|24}}

12
24

---

 44 /

sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = sin 32,3122 0 = 0,5345 24

Schrijfwijze

Het hoofdtelwoord geeft de teller van een breuk weer, het rangtelwoord de noemer.

•  1 / 5  een vijfde,  7 /10 zeven tiende, 1  2 /6 een twee zesde.
• 11  1 /5 elf en een vijfde, elf een vijfde, of elf gehelen en een vijfde.

---

Enkele breuken hebben een eigen naam:

•  1 / 2  half
•  1 / 4  kwart
•  3 /4 driekwart
• 1  1 /2 anderhalf

---

Een derde lijkt een eigen naam te hebben. Het is als breuk een "gewone" combinatie (derde is het rangtelwoord van drie):

•  1 / 3  een derde (dus niet eenderde)
•  2 /3 twee derde.

---

 sina /cosa

•  30-10 /5

 60 /24/60

sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = 0 = 0,5345 24

sin a = sin 32 + 18 +  44 /60/60 = sin 32,3122

Het eerste voorbeeld is ook als volgt toe te lichten: als men twee taarten elk in vier even grote stukken snijdt, resulteert dat in acht stukken. Ook het delen van breuken is zo te beschrijven: als men anderhalve (1 ¹⁄₂ = ³⁄₂) euro uitgeeft aan artikelen die een halve euro per stuk kosten, krijgt men drie van die artikelen, want  3 /2 :  1 / 2  =  3 /2 ×  2 /1 =  3 × 2 /2 × 1 = 3.

Rekenvoorbeeld

Bronvermelding

Bronnen, noten en/of referenties:

• Meetkunde ( Inleiding )
• Meetkunde ( Driehoeken )
• Meetkunde ( Veelhoeken )
• Meetkunde ( De cirkel )
• Rondom de cirkel ( 1 )
• Rondom de cirkel ( 2 )

Een quote is weer heel iets anders.

Een streamer bevat een korte tekst van twee of drie regels.

Dit artikel valt onder beheer van Dorp:Luisterrijk.

a-b a+b	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
λ	1,003	1,010	1,023	1,040	1,064	1,092	1,127	1,168	1,216	1,273

A = 2 π r

dan bevat dus de hele cirkel 2 π radialen, wat overeen komt met 360 graden. Omgekeerd == Bronvermelding ==

Bronnen, noten en/of referenties:

• Meetkunde ( Inleiding )
• Meetkunde ( Driehoeken )
• Meetkunde ( Veelhoeken )
• Meetkunde ( De cirkel )
• Rondom de cirkel ( 1 )
• Rondom de cirkel ( 2 )

geldt ook, dat:

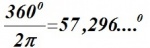
Groter

Op een gegeven moment meent hij, dat hij de zin van het Spel dicht is genaderd, maar denkt toch dat hij dit niet tot zijn beroep moet maken.

1t0PeWRD 1t0PeWRD

<

• Ungarischer Tanz nr.5 op YouTube

Italiano: Scaramuccia Deutsch: Scaramuz Datum 1860(1860)

Quelle SAND Maurice. Masques et bouffons (Comedie Italienne). Paris, Michel Levy Freres, 1860

Urheber Maurice Sand

2 ²/ ₉ + ⁵/ ₉ = 2 ⁷/ ₉

12 ³ • 3 : 9 - √ 36 + 5 - 3 =

128 ⁴/ ₇ ⁰ achtenveertig achtenveertig

• P = U • I • cos φ
• P = 3U _f • I _f • cos φ

waarbij:

• U _f = U _fase en I _f = I _fase
• P = 3 U _fase• I _fase • cos φ

Moon River, Goodnight Moon, Moon Cloud, Dark of the Moon

haiku (senryu, tanka, waka) en poëzie (met name haikus) waarin wordt gestreefd op impressionistische wijze de ware essentie te vangen.

Over de eindigheid van driehoeken

Dit is een gebruikersessay geschreven door Franciscus 30 jan 2015 16:46 (CET)

Inleiding

Δ BCD ~ Δ ABC

Franciscus 7 feb 2015 12:31 (CET)