Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Over de eindigheid van driehoeken
Inleiding
In Meetkunde ( Driehoeken ) wordt de stelling van Pythagoras behandeld. Deze luidt:
- In een rechthoekige driehoek is de som van de kwadraten van de rechthoekszijden gelijk aan het kwadraat van de schuine zijde.
Deze stelling kan met de rechthoekige driehoek (Δ) en de bijbehorende
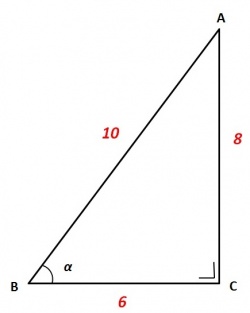
rechthoekszijden BC en AC in een formule worden uitgedrukt, namelijk:
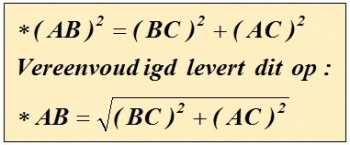
Verdere uitwerking
Voor de hiernaast afgebeelde rechthoekige Δ ABC met zijden BC = 6 en AC = 8, is zijde AB met behulp van deze stelling eenvoudig te berekenen, namelijk:
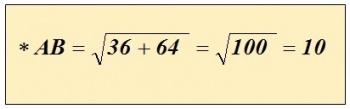
( Voor het inzicht in het verdere verloop van het 'proces', is gebruik gemaakt van getallen. Hierdoor wordt 'grip' gehouden op dit proces. Ter vereenvoudiging zijn ook geen dimensies bij de zijden van de Δ geplaatst. )
Goniometrische basisfuncties
De afgebeelde rechthoekige Δ ABC bevat ook een aantal goniometrische verhoudingen, die ongeacht de afmetingen van de zijden van de Δ geldig zijn, en derhalve dimensieloos zijn. Deze goniometrische verhoudingen dienen onder meer om de hoeken van de Δ te bepalen, maar worden ook voor andere doeleinden gebruikt.
De eerste en meest bekende verhouding wordt aangeduid met de sinus van de hoek α meestal afgekort tot sin α.
De sinus van hoek α wordt als volgt omschreven:

Voor de tweede goniometrische verhouding, cosinus α, afgekort als cos α , geldt:

( In Goniometrie worden de andere goniometrische basisformules verder behandeld. )
Constructie van de naar A voortschrijdende driehoeken
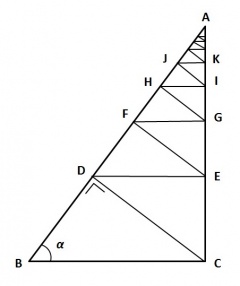
In de rechthoekige Δ ABC zijn de sinus en de cosinus van hoek α nu met eenvoudige goniometrie vast te stellen, zoals dat in de volgende, omkaderde berekening is uitgevoerd.

Als in Δ ABC de loodlijn CD op zijde AB wordt neergelaten,
dan is Δ BCD gelijkvormig aan Δ ABC, aangezien hoek α gemeenschappelijk is en beide
Δ Δ een hoek van 90 0 bevatten. Dit wordt aldus genoteerd: Δ BCD ~ Δ ABC.
Vervolgens kunnen nu de zijden BD en CD
worden afgeleid, namelijk:

Als nu de lijn DE wordt getrokken, parallel aan BC , dan is ook Δ CDE ~ Δ ABC, en geldt het volgende:

Het zal duidelijk zijn, dat – als verdere Δ Δ worden geconstrueerd – dit uiteindelijk zal eindigen in A. Hoe dit in zijn werk gaat, wordt in de volgende stappen uiteengezet.
Stapsgewijs naar limiet 0
Als nu de loodlijn EF wordt getrokken, dan is ook Δ DEF ~ Δ ABC , en geldt het volgende:
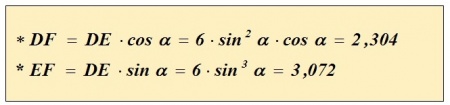
Deze procedure van steeds kleiner wordende Δ Δ kan worden voortgezet totdat de uiterste punt A van Δ ABC wordt bereikt, of met andere woorden:
- In hoekpunt A wordt de limiet = 0 bereikt.
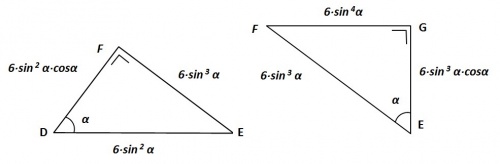
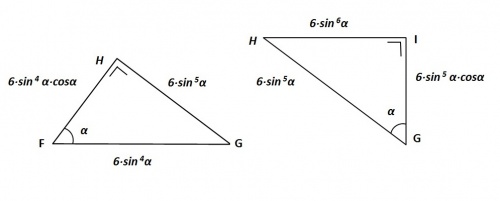
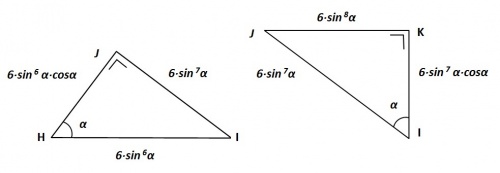
In de bijgaande afleidingen worden van de voortschrijdende Δ Δ de zijden vastgesteld.
( Omwille van de eenvoud, houdt het construeren en berekenen van de opeenvolgende Δ Δ bij Δ JK op )

|

Grafische voorstelling
Bij de reeks berekeningen, lopend tot 6 • sin 100α , wordt het duidelijk, dat ná 6 • sin 50α de getalwaarde naar 0 gaat naderen, of met andere woorden:
- Bij 0 wordt de limiet bereikt van 6 • sin nα
Uit de onderstaande berekeningen kan worden vastgesteld, dat deze limiet al ongeveer bij 6 • sin 100α bereikt wordt.
( In dit kader verdient het de aandacht, te beseffen, dat de gangbare elektronische rekenmachines niet in staat zijn om zeer kleine getallen nog met de vereiste nauwkeurigheid weer te geven. )
In de bijbehorende grafiek is het naderen tot de limiet = 0 nog beter te volgen.

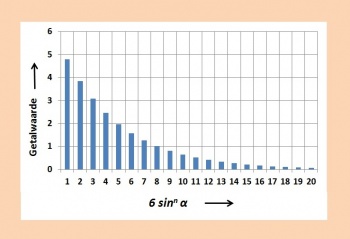
Terecht werd gesteld, dat de limiet al bijna wordt bereikt bij 6 • sin 100α. In theorie is dit echter nog niet het geval. Hoe dat dan werkelijk is, zal hierna in Algemene geldigheid worden uiteengezet.
Algemene geldigheid
In het begin werd aangegeven, dat voor het inzicht in het verloop van het proces, getallen voor de zijden BC en AC nodig waren. Bij de gekozen getalwaarden voor de zijden BC = 6 en AC = 8, blijkt dat ná 6 • sin 50α de getalwaarde naar 0 gaat naderen.
Bij keuze van andere getalwaarden had dit naderen tot 0 ook plaats gevonden, alleen eerder of later dan bij BC • sin 50α .
Het naderen van de limiet 0 is dus voor elke aanliggende rechthoekszijde x - met de bijbehorende getalwaarde - van kracht.
Verder kan worden gesteld, dat de limiet 0 voor elke aanliggende rechthoekszijde x theoretisch pas wordt bereikt als
n is ONEINDIG (∞) geworden.
Dit wordt aldus genoteerd:

Op het moment dat n =∞ , wordt dan gelijkertijd voor de - van de oorspronkelijke rechthoekige Δ ABC afgeleide Δ - de EINDIGHEID bereikt.
Nawoord
- Het blijkt, dat is een rechthoekige Δ , een aantal gelijkvormige Δ Δ kunnen worden aangebracht, die vanuit een hoekpunt - in dit geval hoekpunt B met de hoek α - steeds kunnen worden uitgebreid.
- Uit het onderzoek blijkt verder, dat de zijden x van de gelijkvormige Δ Δ steeds een functie van sinα zijn. Dit wordt aldus geschreven:
- x = f ( sin nα ).
- Bij verdere uitbreiding van de rechthoekige Δ Δ zullen deze uiteindelijk in het tegenoverliggende hoekpunt A eindigen.
- Op dat moment wordt de limiet 0 bereikt - uitgedrukt in bovenstaande formule - en houdt de van de oorspronkelijke Δ ABC afgeleide Δ op te bestaan.

