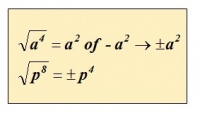Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Algebra ( Machtsverheffen en Worteltrekken )
Machtsverheffen en worteltrekken
In Algebra ( 3 ) werden de bewerkingen Vermenigvuldigen en Delen behandeld. In Algebra ( 4 ) komen Machtsverheffen en Worteltrekken aan de orde.
Machtsverheffen
Machtsverheffen gaat op dezelfde manier als bij het rekenen, namelijk:
Als het grondtal positief is, dan is het product ook positief:
Als het grondtal negatief is, dan is het product:
- Negatief als de exponent buiten de haakjes oneven is
- Positief als de exponent buiten de haakjes even is

Worteltrekken
In Algebra ( 3 ) werd al aangegeven, dat bij het vermenigvuldigen van positieve en negatieve getallen er twee mogelijkheden zijn, namelijk:
- Bij gelijke tekens is de uitkomst positief
- Bij ongelijke tekens is de uitkomst negatief
Dat houdt dus in, dat als bijvoorbeeld de wortel uit 64 wordt getrokken, de uitkomst twee mogelijkheden heeft, namelijk: 8 of - 8.
Dit wordt als volgt aangegeven: ± 8.
.
Bij algebraïsche bewerkingen gaat dit op precies dezelfde manier:
Algebra in formules
Als voorbeeld, hoe Algebra in formules wordt toegepast geldt het volgende voorbeeld. Een zeer bekende stelling in de wiskunde is namelijk de Stelling van Pythagoras.
Deze luidt:
In een rechthoekige driehoek is de som van de kwadraten van de rechthoekszijden gelijk aan het kwadraat van de schuine zijde.
Dit houdt in - dat als van een rechthoekige driehoek twee zijden bekend zijn - met behulp van de stelling van Pythagoras de derde zijde kan worden berekend.
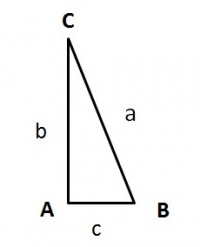
De stelling kan met de rechthoekige driehoek ABC en de bijbehorende rechthoekszijden a,b en c in de vorm van een formule worden uitgedrukt, namelijk:
Links
Algebra ( 1 ) : Inleiding
Algebra ( 2 ) : Optellen en aftrekken
Algebra ( 3 ) : Vermenigvuldigen en delen
Algebra ( 5 ) : Vergelijkingen
Algebra ( 6 ) : Merkwaardige producten