Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Visualisatie van irrationale getallen: verschil tussen versies
(Nieuwe pagina aangemaakt met '{{essay|Franciscus oktober 2013 15:02 (UTC)}} =Visualisatie van irrationale getallen= ==Inleiding== Het begrip '''''visualisatie''''' heeft een aantal betekenissen, a...') |
|||
| Regel 1: | Regel 1: | ||
{{essay|Franciscus oktober 2013 15:02 (UTC)}} | {{essay|Franciscus oktober 2013 15:02 (UTC)}} | ||
==Inleiding== | ==Inleiding== | ||
Het begrip '''''visualisatie''''' heeft een aantal betekenissen, als: | Het begrip '''''visualisatie''''' heeft een aantal betekenissen, als: | ||
Versie van 8 okt 2013 13:23
Inleiding
Het begrip visualisatie heeft een aantal betekenissen, als:
- in een beeld zichtbaar maken van een gedachte
- iets beeldend voorstellen
- iets aanschouwelijk maken
- iets zichtbaar maken
- iets uitbeelden
- iets voorstellen
- het vertalen van een gedachte naar een beeld, een uitdrukkingsvorm
- een visuele weergave in de vorm van een afbeelding, een afdruk, een figuur, een illustratie of een tekening
In dit essay zal - geleid door bovenstaande definities - getracht worden enkele bijzondere irrationale getallen te visualiseren.
Rationale en irrationale getallen
Rationale getallen zijn getallen, die als het quotiënt van twee gehele getallen zijn te schrijven, zoals:
72/36 = 2/1 = 2
- Rationaal - afkomstig van Ratio ( Latijn voor: de rede, het denken, berekenbaar ) - betekent hier: volledig berekenbaar, meetbaar.
Elk rationaal getal is op één manier te schrijven als een onvereenvoudigbare breuk met een positieve noemer.
Naast rationale getallen als:
12, 45, 100 .......
etcetera, bestaan er ook getallen die niet rationaal zijn, zoals:
√2,√3, π, log 5, e, φ
waarbij e het grondtal van de natuurlijke logaritme is, en φ de basis vormt van de Gulden Snede.
- Deze getallen - die niet als een breuk kunnen worden geschreven – zijn repeterende getallen die oneindig blijven doorgaan en transcedent zijn. Dat houdt in, dat deze getallen niet als een verhouding van twee hele getallen te schrijven zijn, en dat in de cijfers achter de komma geen zich herhalend patroon voorkomt.
- Het zijn zijn dus getallen, die niet in het decimale stelsel zijn uit te drukken. Deze getallen worden irrationale getallen genoemd.
Visualisatie van wortels
Het bijzondere bij irrationale getallen is, dat – als het lukt deze in een geometrisch figuur onder te brengen - dit oneindige karakter niet meer is terug te vinden. Als voorbeeld geldt hier de visualisatie van wortels. Bekend zijn vooral deze wortels:
√2 = 1,41421356……..
en:
√3 = 1,73050808……..

In een willekeurig vierkant met zijden α kan een diagonaal worden getekend en berekend. De zijde α is onbepaald, maar kan elke grootte hebben. Voor het gemak kiezen we hiervoor het getal 1. De diagonaal d1 van het zwarte vierkant is nu op eenvoudige manier met Pythagoras te berekenen, namelijk:

Als diagonaal d 1 vanuit de linker onderhoek wordt omgecirkeld, dan is dus ook de onderste zwarte lijn en de oranjelijn samen gelijk aan:
a√2 = √2
De diagonaal d2 van de nieuwe rechthoek is eveneens op eenvoudige manier te berekenen, namelijk:

Als nu diagonaal d2 vanuit de linkeronderhoek wordt omgecirkeld, dan is dus ook de onderste zwarte lijn + de oranjelijn + de groene lijn samen gelijk aan:
√3
Als deze procedure wordt voortgezet, dan ontstaan vervolgens de vormen:
√4 = 2
en:
√5
enzovoort.
- Door middel van een eenvoudige geometrische figuur, is het mogelijk gemaakt, wortels - met hun niet-eindigende reeks getallen achter de komma - zodanig te visualiseren, dat het oneindige karakter hiervan niet meer zichtbaar is.
Visualisatie van het getal π

Een van de kenmerken van een cirkel is, dat de omtrek:
O = 2 π r
en het oppervlak:
A = π r 2
waarbij r de straal van de cirkel is. Deze straal is als regel een rationaal getal.
Het getal π is een irrationaal en repeterend getal, waaraan geen einde komt.
- Met een computer is het tegenwoordig niet al te moeilijk een miljoen decimalen van π te berekenen. Of je daar veel mee kan doen, is natuurlijk weer heel iets anders. Voor praktische doeleinden is het rekenen met 3,14159….. voor de meeste toepassingen al ruim voldoende.
- Met zo ongeveer 200 decimalen de letter π uit te beelden - zoals hiernaast is gedaan - is natuurlijk veel aardiger dan een oneindige reeks decimalen te berekenen!
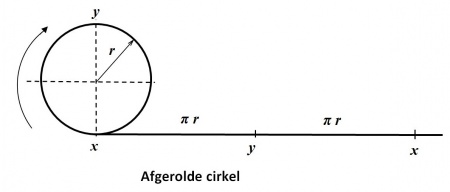
Als een cirkel wordt afgerold over een vlak, dan wordt de cirkelboog gestrekt en is deze gestrekte boog dus:
x y = π r
en de boog:
y x = π r
en dus bij een volle omwenteling:
x x = 2 π r
- Het getal π - met zijn niet-eindigende reeks getallen achter de komma - is hier via de cirkel, de uitbeelding via een lettervorm en de afwikkeling tot een rechte lijn gevisualiseerd. Hierdoor is het oneindige karakter van π niet meer zichtbaar.
Visualisatie van logaritmen
In Rekenkunde ( 3 ) wordt het onderwerp Worteltrekken behandeld, waarbij als voorbeeld de wortel uit 10 wordt genomen, aldus:
√10 = 3,1622....
Een andere schrijfwijze voor de wortel uit 10 is:
10 1/2 = 10 0,5
wat hetzelfde oplevert, namelijk:
3,1622....
Op deze manier kan bij logaritmen elk getal worden uitgedrukt met het grondtal 10 voorzien van een exponent.
Zo levert de exponent 0,3010.... het getal 2 op, aldus:
10 0,3010.... = 2
of bijvoorbeeld:
10 0,6989.... = 5
De exponent van het grondtal wordt hier mantisse genoemd. Deze zijn in tabellen terug te vinden.
- Tegenwoordig wordt er niet meer zo uitgebreid gebruik gemaakt van deze tabellen maar meer van ( wetenschappelijke ) calculators.
- In Logaritmen en exponentiële functies worden uitgebreid de voornaamste bijzonderheden van logaritmen behandeld en wordt duidelijk, dat bij logaritmen de mantisse altijd een irrationaal getal is.

Om een logaritme te visualiseren, is bijbehorende grafiek - met een horizontale lineaire x-as en een verticale logaritmische y-as – is het gebied tussen:
10 0 = 1
en
10 2 = 100
weergegeven. Dit wordt door de logaritmische schaal een rechte lijn.
Als de mantisse =
1
dan is dus het bijbehorende getal =
10 1 = 10
Bij het getal
10 2 = 100
is de mantisse =
2
Bij bijvoorbeeld het getal 3, is de mantisse iets kleiner dan 0,5, namelijk:
0,4771...
Als log 30 in de grafiek wordt opgezocht, blijkt dit < 1,5 te zijn, namelijk: 1,4771….
1,4771...
- Het visualiseren van logaritmen is hier door middel van een grafische voorstelling gerealiseerd.
Visualiseren van de constante e
Het bijzondere getal e – ook wel de constante e genoemd – is het grondtal van de natuurlijke logaritme. In Logaritmen en exponentiële functies wordt daar nader op ingegaan.
De constante:
e = 2,7182818.....
blijkt ook weer een irrationaal getal te zijn.
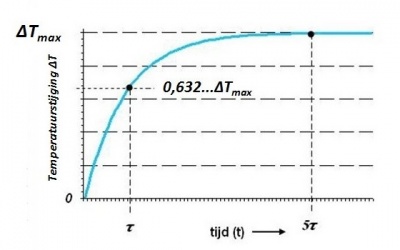
In een zogenaamde e-kromme, wordt het verband tussen bijvoorbeeld tijd en toename getoond, die aanwezig zijn bij de meeste natuurlijke processen, zoals de temperatuurstijging ΔT van een ruimte of een object. Dit verband wordt uitgedrukt in de volgende vorm:
ΔT = ΔT max ( 1 - e -t/τ )
waarbij τ de zogenaamde tijdconstante is. Als de tijd t de tijdconstante τ bereikt, dan is:
ΔT = ΔT max ( 1 - e -1 ) = ( 1 - 0,3678.... )
= 0,632....ΔT max
Bij ongeveer:
5t
blijkt
ΔT max
bereikt te worden.
- Een vrij ingewikkelde formule, behorende bij het irrationale getal e, laat zich in een grafische voorstelling op eenvoudige wijze lezen, waardoor onmiddellijk inzicht ontstaat in het achterliggende proces.

Visualisering van het getal Φ
In 1202 publiceerde Leonardo van Pisa - bijgenaamd Fibonacci - zijn Liber Abaci ( Boek der berekeningen ). In dit boek komt hij uit op een reeks waarbij elke term de som is van de twee voorgaande termen, aldus:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610….
Deze reeks blijft groeien, doordat deze steeds teruggrijpt op de voorafgaande getallen.
De rij of reeks ziet er eigenlijk heel gewoon uit, totdat onderzocht wordt hoe het staat met de verhouding tussen steeds twee opeenvolgende getallen, te beginnen met 2:
| Quotiënt | Getal |
| 2/1 | 2 |
| 3/2 | 1,5 |
| 5/3 | 1,666... |
| 8/5 | 1,6 |
| 13/8 | 1,625... |
| 21/13 | 1,615... |
| 34/21 | 1,619... |
| 55/34 | 1,6176... |
| 89/55 | 1,61818... |
| 144/89 | 1,61797... |
| 233/144 | 1,61805... |
| 377/233 | 1,618025... |
| 610/377... | 1,61803...
|
Het bijzondere getal 1,61803….., - voortkomend uit de oplopende reeks quotiënten - wordt Φ ( phi ) genoemd. Verdere quotiënten leveren geen verdere verfijningen meer op, zodat met 1,61803 wel de limiet is bereikt.
Er blijken enkele eigenschappen met Φ te zijn verbonden.
De eerste eigenschap die opvalt en grote bekendheid heeft verkregen is de zogenaamde Gulden Snede. De constructie van zo'n Gulden Snede wordt via een driehoek met rationale getallen uitgevoerd. Deze constructie wordt hier achterwege gelaten.

- De Gulden Snede verdeelt een lijnstuk in twee delen, waarvan het grootste deel φ middelevenredig is tussen het kleinste deel en de gehele lijn. Bij de middelevenredige zijn de middelste termen aan elkaar gelijk.
Als voor het gemak hier voor het kleinste deel het getal 1 wordt gekozen, dan wordt de vorm dus:
1 : φ = φ : ( φ + 1 )
waaruit dan volgt:
φ 2 = ( φ + 1 ) . 1
en dus:
1,61803... 2 = 1,61803...+ 1 = 2,61803...
Het is natuurlijk merkwaardig, dat het kwadraat van φ net zo groot is als φ + 1 = 2,1683...!
- De gulden snede zou - volgens sommigen - een bijzondere schoonheid bezitten en komt veel voor in klassieke architectuur, schilderkunst en in de levende natuur, waarbij zelfs het ideale menselijke lichaam volledig volgens de guldensnede-verhouding zou zijn opgebouwd. Ook beelden uit het oude Griekenland worden soms in verband gebracht met de gulden snede.
- In de loop van de twintigste eeuw verwierf de gulden snede een plaats in diverse vormen van kunstonderwijs en in de architectuur. Ook in de reclame heeft de verdeling een plek gevonden.
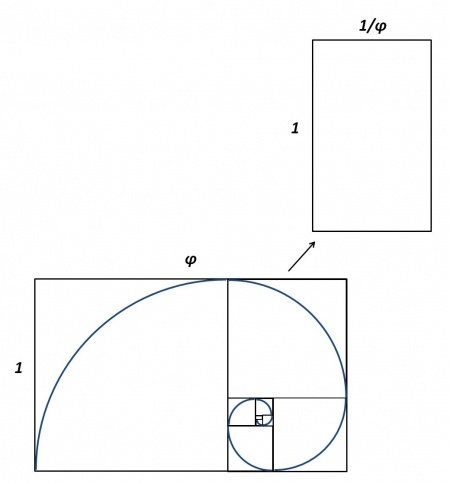

>>>>>>>Nautilusschelp
De lijnstukken van de middelevenredige vorm kunnen worden omgezet naar een rechthoek met de lange zijde =
φ
en de korte zijde =
1
Vervolgens kan in deze rechthoek een kleinere rechthoek worden geplaatst die dezelfde verhouding heeft en waarvan de lange zijde =
1
en de korte zijde dus:
1/φ
Op dat moment ontstaat er in de oorspronkelijke rechthoek een vierkant, aangezien de lange zijde nu wordt:
φ – ( 1/φ ) = 1
en de korte zijde =
1
Als op deze manier wordt doorgegaan, dan ontstaat een steeds kleiner wordende draaiende rechthoek, waarin zich een spiraal ontwikkelt, als – te beginnen links onder – een vloeiende lijn wordt getrokken in het vierkant. Zo’n spiraal is terug te vinden in bijvoorbeeld de Nautilusschelp en meer vormen uit de natuur.
- De tabel en de verdeling van een eindig lijnstuk in φ , 1 en de constructie van een spiraal uit draaiing van rechthoeken, laten zien, dat het bijzondere irrationale getal φ op eenvoudige manier zichtbaar gemaakt kan worden.
- In de taal van de symbolen werd en wordt de spiraal dikwijls verbonden met sterven herboren worden. Ook dacht men vroeger, dat de lichamelijke en spirituele energie in spiraalvorm stroomde.
Nawoord
In de wiskunde en vooral bij de meetkunde, is het - om de theorie te ondersteunen - noodzakelijk om met afbeeldingen te werken. Als regel betreft dit afbeeldingen van geometrische figuren.
In dit essay is getracht enkele specifieke irrationale getallen te visualiseren. Hierdoor ontstaat meer inzicht in deze bijzondere getallen en de wijze waarop deze een plaats innemen in de wiskunde.

