Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Rondom de cirkel ( 1 ): verschil tussen versies
Geen bewerkingssamenvatting |
Geen bewerkingssamenvatting |
||
| Regel 57: | Regel 57: | ||
==Radialen== | ==Radialen== | ||
[[Afbeelding:AB.jpg|right|200px]] | [[Afbeelding:AB.jpg|right|200px]] | ||
Als van een cirkel de straal '''''r''''' aan de buitenzijde wordt afgewikkeld, dan zal de middelpuntshoek '''''ω''''' een vaste waarde omvatten. De hoek '''''ω''''' wordt uitgedrukt in radialen. | Als van een cirkel de straal '''''r''''' aan de buitenzijde wordt afgewikkeld, dan zal de middelpuntshoek '''''ω''''' een vaste waarde omvatten. De hoek '''''ω''''' wordt uitgedrukt in '''''radialen''''''. | ||
<br/>Een radiaal is dus de hoek '''''ω''''' die gevormd wordt door de boog A-B van de cirkel waarbij die boog precies even lang is als de straal '''''r''''' van | <br/>Een radiaal is dus de hoek '''''ω''''' die gevormd wordt door de boog A-B van de cirkel waarbij die boog precies even lang is als de straal '''''r''''' van die cirkel.'' | ||
De radiaal wordt ook aldus beschreven: | De radiaal wordt ook aldus beschreven: | ||
:*''Een radiaal ( rad ) is de vlakke hoek tussen twee stralen '''r''' van een cirkel die op de omtrek een boog afsnijden, waarvan de lengte gelijk is aan de straal '''r'''. | |||
Een hoek in radialen | :*''Een hoek in radialen kan dus ook omschreven worden, als de verhouding tussen '''booglengte''' en '''straal'''. | ||
Dit maakt de radiaal tot een een dimensieloos getal, wat zeer handig is in formules, die hierdoor een eenvoudiger gedaante hebben. | |||
<br/>Als de boog '''''A-B''''' = '''''r''''', en de omtrek van een cirkel is: | <br/>Als de boog '''''A-B''''' = '''''r''''', en de omtrek van een cirkel is: | ||
<br/> | <br/> | ||
| Regel 68: | Regel 68: | ||
<span> | <span> | ||
<font> | <font> | ||
<span style="font-size:150%;"><font color=black>''''' | <span style="font-size:150%;"><font color=black>'''''O = 2 π r''''' | ||
</font> | </font> | ||
</span> | </span> | ||
| Regel 75: | Regel 75: | ||
dan bevat dus de hele cirkel '''''2 π''''' radialen, wat overeen komt met 360 graden. Omgekeerd geldt ook, dat: | dan bevat dus de hele cirkel '''''2 π''''' radialen, wat overeen komt met 360 graden. Omgekeerd geldt ook, dat: | ||
[[Afbeelding:Radiaal.jpg|left|150px]] | [[Afbeelding:Radiaal.jpg|left|150px]] | ||
<br/> | |||
<br/> | <br/> | ||
<br/> | <br/> | ||
Versie van 4 okt 2013 14:46
Dante Alighieri heeft ooit geschreven: Lo cerchio è perfettisima figura, ofwel: De cirkel is de meest volmaakte figuur.
Als we in het woordenboek bij het woord cirkel uitkomen, dan zien we daar staan: gesloten kromme lijn, waarvan alle punten op eenzelfde afstand van één punt, het middelpunt liggen. Dat laat dus weinig speelruimte over. Bij het woord volmaakt zien we vervolgens staan: voortreffelijk, uitmuntend, voltooid, volledig, volkomen.
Al is de cirkel volgens Dante dan het meest volmaakte figuur, hij kent toch ook in zekere zin zijn beperkingen. Anders dan rond kan een cirkel namelijk niet zijn, anders houdt deze figuur op een cirkel te zijn. Een cirkel kan wel oneindig klein of oneindig groot zijn maar zal voor praktische doeleinden meestal hier ergens tussenin liggen, waaruit dan weer blijkt, dat je ook bij de cirkel grenzen moet stellen.
Het bijzondere bij een cirkel is, dat er bij berekeningen een bijzonder getal aan te pas moet komen, namelijk de wiskundige constante π. Deze constante, een getal zonder einde, intrigreert al duizenden jaren menige wiskundige.
Op veel plaatsen in de wiskunde, de natuurkunde en in de techniek is het getal π onmisbaar.
Benadering van de constante π
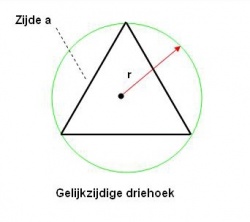
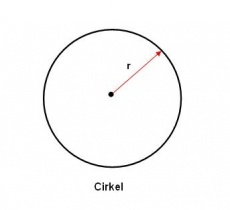
Om enig inzicht in het getal π te krijgen, is een uitstapje naar de eenvoudige wiskunde nodig. Op de eerste afbeelding is een willekeurige cirkel weergegeven met de straal r.
Eén zijde a van een gelijkzijdige driehoek die precies in een cirkel past, heeft een lengte van r√3, zodat dus de drie zijden van de driehoek samen 3 . a = 3√3r groot zijn ofwel : de omtrek = 5,196r. Je zou ook voor het gemak kunnen schrijven dat de omtrek = 5,196r/2 = 2,598d, aangezien d ( = 2r ) de middellijn van de cirkel is. Het blijkt namelijk, dat met d werken wat hanteerbaarder is dan met r.
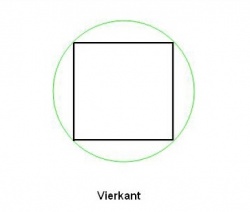
Als je een vierkant neemt en deze in een cirkel plaatst, dan geldt, dat één zijde ervan = r√2, zodat de vier zijden van het vierkant samen ( de omtrek dus ) 4r√2r zijn of in d uitgedrukt: 2,828d.
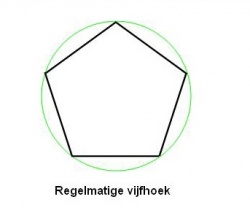
Bij een regelmatige vijfhoek blijkt de omtrek hiervan 2,94d te zijn. Ga je nog verder met regelmatige veelhoeken als een zeshoek, een achthoek, een tienhoek, een twaalfhoek, een vierentwintighoek, een zesendertighoek, een tweeënzeven-tighoek, een driehonderdzestighoek, een zevenhonderdtwintighoek, tot een zesendertighonderdhoek, dan blijkt, dat naarmate het aantal hoeken groter wordt, de wiskundige constante steeds meer nadert tot het getal 3,14159. Voor het gemak is men deze constante π gaan noemen.
In de tabel is van een aantal regelmatige veelhoeken nagegaan hoe het met die constante staat. Algemeen geldt hierbij, dat de omtrek = n . a, waarbij n het aantal zijden van de veelhoek is.
| Regelmatige veelhoek | Omtrek ( n . a ) | Wiskundige constante |
|---|---|---|
| Gelijkzijdige driehoek | 2,598d | 2,598 |
| Vierkant | 2,828d | 2,828 |
| Vijfhoek | 2,94d | 2,94 |
| Zeshoek | 3,0d | 3,0 |
| Achthoek | 3,06d | 3,06 |
| Tienhoek | 3,09d | 3,09 |
| Twaalfhoek | 3,108d | 3,108 |
| Vierentwintighoek | 3,1326d | 3,1326 |
| Zesendertighoek | 3,1376d | 3,1376 |
| Tweeënzeventighoek | 3,1406d | 3,1406……. |
| Driehonderzestighoek | 3,14155d | 3,14155……. |
| Zevenhonderdtwintighoek | 3,14158d | 3,14158……… |
| Zesendertighonderdhoek | 3,14159d | 3,14159…… ( π ) |
Uit deze eenvoudige benadering blijkt, dat in het begin de constante vrij snel stijgt, maar dat na een 72-hoek de stijging nog maar gering is. Het constante getal 3,14….. gaat hierna langzaam naderen tot het ons bekende getal π, waarbij er steeds meer decimalen bijkomen.
Vergelijking met de cirkelboog
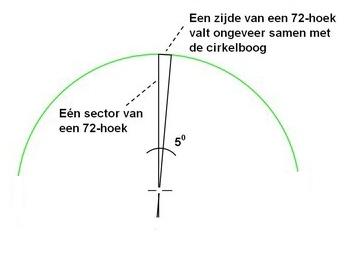
Uit de tabel blijkt al, dat naarmate het aantal hoeken van de veelhoek groter wordt, het constante getal π steeds meer in zicht komt. Dit houdt ook in, dat elk rechte lijnstukje van de veelhoek dat op de cirkel ligt, steeds meer op een cirkelboogje gaat lijken, waardoor
uiteindelijk de zijden van de veelhoek samenvallen met de cirkelbogen.
Bij een tweeënzeventighoek is, zoals de tabel laat zien, de constante al aardig op weg naar de wiskundige constante π .
In de afbeelding is één sector van deze veelhoek weergegeven. Als een zijde van die veelhoek en de bijbehorende cirkelboog wordt vergeleken met bijvoorbeeld een zijde van een vierkant of een regelmatige vijfhoek, dan is het verschil wel duidelijk: bij de tweeënzeventighoek valt een zijde ervan ongeveer samen met de cirkelboog, terwijl bij het vierkant of de vijfhoek nog een groot verschil aanwezig is.
Het irrationale getal π
In wiskundige termen uitgedrukt, is de wiskundige constante π een irrationaal getal, dat zelfs transcendent is. Dit houdt in dat π niet als een verhouding van twee hele getallen te schrijven is en dat in de decimale voorstelling geen zich herhalend patroon voorkomt. De waarde van π kan daarom in decimale notatie alleen benaderd worden, want de reeks cijfers achter de komma is oneindig lang.

Met een computer is het tegenwoordig niet al te moeilijk een miljoen decimalen van π te berekenen. Of je daar veel mee kan doen, is natuurlijk weer heel iets anders. Voor praktische doeleinden is het rekenen met 3,14159….. voor de meeste toepassingen al ruim voldoende.
Met zo ongeveer 200 decimalen de letter π uit te beelden - zoals hiernaast is gedaan - is natuurlijk veel prettiger dan een oneindige reeks decimalen te berekenen!
Radialen

Als van een cirkel de straal r aan de buitenzijde wordt afgewikkeld, dan zal de middelpuntshoek ω een vaste waarde omvatten. De hoek ω wordt uitgedrukt in radialen'.
Een radiaal is dus de hoek ω die gevormd wordt door de boog A-B van de cirkel waarbij die boog precies even lang is als de straal r van die cirkel.
De radiaal wordt ook aldus beschreven:
- Een radiaal ( rad ) is de vlakke hoek tussen twee stralen r van een cirkel die op de omtrek een boog afsnijden, waarvan de lengte gelijk is aan de straal r.
- Een hoek in radialen kan dus ook omschreven worden, als de verhouding tussen booglengte en straal.
Dit maakt de radiaal tot een een dimensieloos getal, wat zeer handig is in formules, die hierdoor een eenvoudiger gedaante hebben.
Als de boog A-B = r, en de omtrek van een cirkel is:
O = 2 π r
dan bevat dus de hele cirkel 2 π radialen, wat overeen komt met 360 graden. Omgekeerd geldt ook, dat:
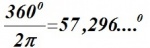
Link
- In Rondom de cirkel ( 2 ) neemt de cirkel alweer een bijzondere plaats in. Het blijkt namelijk, dat van alle regelmatige veelhoeken de cirkel de meest gunstige verhouding tussen oppervlak en omtrek bezit.
![]()
![]() Zie ook de categorie met mediabestanden in verband met Unit circles op Wikimedia Commons.
Zie ook de categorie met mediabestanden in verband met Unit circles op Wikimedia Commons.
![]()
![]() Zie ook de categorie met mediabestanden in verband met Circle geometry op Wikimedia Commons.
Zie ook de categorie met mediabestanden in verband met Circle geometry op Wikimedia Commons.
