Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Gebruiker:Franciscus/kladblok: verschil tussen versies
Geen bewerkingssamenvatting |
Geen bewerkingssamenvatting |
||
| Regel 1: | Regel 1: | ||
| Regel 27: | Regel 13: | ||
==Jean Cocteau== | |||
[[Afbeelding: Jean Cocteau 1923.jpg|250px|thumb|right|<big>Jean Cocteau in 1923]] | |||
Jean Maurice Eugène Clément Cocteau (Maisons-Laffitte, 5 juli 1889 – Milly-la-Forêt, 11 oktober 1963) was een Frans dichter, romanschrijver, toneelschrijver, schilder, ontwerper en filmmaker. Cocteau heeft in zijn leven enorm veel geschreven en geproduceerd, en was thuis in bijna alle kunstvormen en was één van de belangrijkste personen binnen het [[Surrealisme|surrealisme]]. | |||
<br/>Zijn bekendste werken zijn het boek ''Les Enfants terribles'' (1929), het toneelstuk ''Les parents terribles'' en de film ''La Belle et la Bête'' (1946). | |||
<br/>Cocteau is een tot de verbeelding sprekend kunstenaar. Maar meer nog dan om zijn werk was Cocteau bekend om zijn opmerkelijke leven. Hij omgaf zich met beroemdheden als [[Sergei Diaghilev]] van de Ballets Russes, de zangeres [[Edith Piaf]] en de schilder [[Pablo Picasso]], en hij raakte geregeld in opspraak vanwege zijn homoseksualiteit en zijn drugsgebruik. | |||
==Afkomst en jeugd== | |||
Jean Cocteau, zoon van Georges en Eugénie Cocteau, werd op 5 juli 1889 geboren in Maisons-Laffitte, in het noordwesten van het stedelijk gebied van Parijs. Het echtpaar had al twee kinderen: Marthe, geboren in 1877 en Paul, geboren in in 1881. | |||
<br/>Het gezin woonde in de winter samen met hun grootouders van moederszijde in een herenhuis in Parijs en in de zomer in Maisons-Laffitte. | |||
<br/>Zijn familie was van een solide Parijse bourgeoisie: gecultiveerd, rijk en geïnteresseerd in muziek, schilderkunst en literatuur. Zijn vader - een jurist - tekent uit liefhebberij en op jonge leeftijd begint Jean dat ook te doen. Zijn grootvader is een muziekliefhebber die muzikale sessies in het huis organiseert. | |||
{{infobox}} | |||
| | |||
<font color=blue> | |||
<span> | |||
<font> | |||
:<span style="font-size:150%;"><font color=blue>''Zijn familie was van een solide Parijse bourgeoisie: gecultiveerd, rijk en geïnteresseerd in muziek, schilderkunst en literatuur'' | |||
</font> | |||
<span> | |||
|} | |||
Jean was een verwend maar nerveus kind. Hij had een grillig karakter en was vaak ziek. | |||
<br/>De vroegste herinneringen van Cocteau hadden te maken met het theater in populaire vormen, zoals het circus en het ijspaleis, en met serieuze theaters, zoals de tragedies die werden uitgevoerd bij de ''Comédie-Française''. | |||
<br/>Op 5 april 1898 - als Jean 9 jaar oud is - pleegt zijn vader zelfmoord. De reden daarvoor is nooit opgehelderd. Het bleef een duister raadsel dat hem altijd blijft achtervolgen en grote invloed op Cocteau heeft uitgeoefend. | |||
<br/>In het voorjaar sterft grootmoeder Lecomte. De grootvader blijft bij zijn dochter wonen. Hij zorgt voor Jean en neemt hem elke zondag mee naar concerten op het conservatorium. Op de Wereldtentoonstelling in Parijs van 1900 is Cocteau vol ontzag voor de dansvoorstellingen. | |||
<br/>Na een periode van basisonderwijs - die in alle opzichten onder het gemiddelde lag en vaak werd onderbroken door slechte gezondheid - begint hij zijn eerste jaar op de middelbare school aan de Lycée Condorcet. Hij blinkt uit in slechts drie onderwerpen: tekenen, gymnastiek en Duits. Zijn leraren vinden hem intelligent, maar inconsistent, onoplettend en rusteloos. | |||
==Eerste publicaties== | |||
De toneelspeler Edouard Max introduceerde de 17-jarige Cocteau in de elitewereld van Parijs. Hij organiseerde een séance rond Cocteaus poëzie, waardoor hij in één keer naam maakte. Zonder hem had Cocteau vast nog een lange weg te gaan gehad door al leurende bij uitgevers aan te kloppen. | |||
<br/>Cocteau wordt wel gezien als het product van de jaren onmiddellijk voorafgaand aan de Eerste Wereldoorlog; jaren van verfijnde artistieke smaak, zonder politieke onrust. Er heerste een idealistische en optimistische geest in Europa. Die periode werd ook wel de ''roaring twenties'' genoemd. | |||
<br/>Zijn echte verkenning van de wereld van het theater begon, toen hij met de ''Ballets Russes''<sup> 1)</sup> in aanraking kwam, geleid door ''Sergei Diaghilev''. Toen Cocteau de wens uitsprak om balletten te maken, daagde Diaghilev hem uit met: "Etonne-moi" ("Verras me").In 1911 schreef hij het libretto voor ''Le dieu bleu'', een ballet voor de Ballets Russes. | |||
==Eerste Wereldoorlog== | |||
Toen de Eerste Wereldoorlog bezig was, wilde Cocteau het leger in, maar werd afgekeurd. Hij wist een burgerkonvooi te organiseren om aan de frontlinie gewonden op te halen, waarbij hij als chauffeur fungeerde. Dat hield hij vol tot 1917. | |||
<br/>Midden in de oorlog kwam Cocteau met ''Parade'' uit, een avant-gardeballet, waarvoor onder anderen [[Pablo Picasso]] de decorstukken en de kostuums ontwierp en [[Erik Satie]] de muziek componeerde. Cocteau en Picasso sloten zich aan bij de groep Ballets Russes van Sergei Diaghilev in Rome om het ballet voor te bereiden. De première van de Parade vond plaats op 18 mei 1917 in het ''Théâtre de Châtelet''. Het publiek en de critici waren meer overbluft dan geërgerd door de muziek van Satie en de sets en kostuums van Picasso. De moderne muziek, het decor, het verhaal; alles was modern en het publiek wist er nog geen raad mee. | |||
<br/>Op 12 juli van dat jaar zijn Jean Cocteau, de dichter en schrijver [[Guillaume Apollinaire]] en de dichter, schrijver en schilder [[Max Jacob]], getuigen bij het huwelijk van Pablo Picasso en [[Olga Koklova]]. | |||
==Kritiek== | |||
Op een gegeven moment schetst Cocteau in 1919 zijn eigen specifieke kunstgevoel. Ondanks zijn inspanningen om betrokken te worden bij de publicatie van een belangrijk document daarover, wordt Cocteau buitengesloten. In die tijd ook publiceert de schrijver [[André Gide]] - een Nobelprijswinnaar - een open brief aan Jean Cocteau in de ''Nouvelle Revue française'' waarin hij de dichtbundel ''Le Cap de Bonne-Espérance'' (Kaap de Goede Hoop) en het ballet ''Parade'' bekritiseert. In hetzelfde artikel citeert Gide ''Le Coq et le Arlequin'' (De haan en de harlekijn) als bewijs dat de dichter geen muzikale vaardigheden bezit. Cocteau reageert hierop fel in het literaire tijdschrift ''Les Ecrits nouveaux'' , waarop Gide natuurlijk terugschiet. Voor Cocteau sluit deze vervelende polemiek tijdelijk de deur naar de ''Nouvelle Revue française'' , waarvoor hij bijdragen leverde. | |||
==Productie== | |||
In 1920 ontmoet hij de zestienjarige Raymond Radiguet, wat uitgroeit tot een liefdesverhouding. In datzelfde jaar wordt Cocteau de verdediger en grote inspirator van jonge musici, die al snel bekendheid verwerven als de "[[Groupe de Six]]". | |||
Hij brengt juni en het grootste deel van juli door in Londen met [[Darius Milhaud]] om de Engelse productie van ''Le Bœuf sur le toit'' in het London Coliseum te verfijnen. | |||
In oktober komt Cocteau uit met het boek ''Thomas l'imposteur'' (Thomas de bedrieger), waar in 1964 ook een film van is gemaakt. | |||
<br/>Op 12 december sterft Radiguet bij gebrek aan onvoldoende medische begeleiding aan tyfus. De totaal ingestorte Cocteau woont de begrafenis niet bij. | |||
Enige tijd later nemen Serge Diaghilev, Auric en Poulenc een radeloze Cocteau mee naar Monte-Carlo. Ze geven hem de raad om troost te zoeken in de opium, wat bij Cocteau tot verslaving leidt. Intussen werkt hij aan plannen voor het ballet ''Le Train bleu''. | |||
In 1925, ondergaat Cocteau - op aandringen van vrienden - een behandeling voor zijn opiumverslaving in de ''Clinique des Thermes Urbains''. | |||
{{infobox}} | |||
| | |||
<font color=blue> | |||
<span> | |||
<font> | |||
:<span style="font-size:150%;"><font color=blue>'' Een periode van intense creativiteit volgt waarin veel werk van hem wordt gepubliceerd'' | |||
</font> | |||
<span> | |||
|} | |||
Een periode van intense creativiteit volgt waarin veel werk van hem wordt gepubliceerd. In het jaar daarna schrijft hij het libretto voor de opera-oratorium ''Oedipus Rex'' voor Stravinsky die vanaf half januari aan de muziek werkt. In mei 1927 was de première, waarbij het werk niet onverdeeld gunstig werd ontvangen. | |||
In december vond in de ''Galerie des Quatre Chemins'' een tentoonstelling van ongewone objecten en tekeningen plaats met de titel ''Poésie plastique'' (Gebeeldhouwde poëzie). Het was een eerste pogingen van Cocteau tot creatie van een moderne post-kubistische kunst in Frankrijk | |||
Op 16 december 1927 première van de opera Pauvre matelot (The Poor Sailor), met muziek van Darius Milhaud. Cocteau voltooit La voix humaine (The Human Voice) en schrijft Le Livre blanc (The White Book). Op 28 december gaat de opera Antigone in première in het Théâtre de la Monnaie in Brussel met muziek van [[Arthur Honneger]]. | |||
Eind november 1928 checkt hij in bij een kliniek in Saint-Cloud in voor een nieuwe poging tot afkicken. | |||
1929 Maakt tekeningen, begint aan het boek ''Opium, journal d'une désintoxication '' en schrijft in drie weken ''Les Enfants terribles'' (Children of the Game), dat zeer gunstig wordt ontvangen. In het boek Opium beschrijft Cocteau's het herstel van zijn verslaving aan opium. | |||
Eind augustus 1931 blijkt hij besmet te zijn met tyfus en moet hij veertig dagen in een kliniek doorbrengen. Kort daarop begon hij weer met opium te roken. In 1933 ondergaat hij weer een kuur om daar van af te raken. | |||
Terwijl ze audities houden voor Oedipus Rex, merkt Cocteau Jean Marais op, en geeft hem een rol in het koor. | |||
==Cineast== | |||
Cocteau debuteerde pas op de relatief late leeftijd van 41 jaar als cineast. Cinema was destijds nog relatief jong, maar de regels van het medium leken al vast te liggen. Cocteau ging echter dapper en volstrekt autodidact zijn eigen koers, en heeft vervolgens een klein maar interessant oeuvre bij elkaar gefilmd. Zijn films worden tegenwoordig nog steeds bekeken en gewaardeerd vanwege hun unieke stijl en sfeer. ''La Belle et la Bête'', ''Orphée'' en andere films waren succesvol De film ''Orphée'' uit 1950 wordt algemeen beschouwd als zijn meesterwerk. Het is een zichzelf mythologiserend portret van de gekwelde kunstenaar, die te kampen heeft met innerlijke demonen, zijn schrijverschap, liefde, dood en de confrontatie met zijn publiek. | |||
==Laatste jaren== | |||
Tijdens de herfst van zijn leven leidt Cocteau een betrekkelijk rustig bestaan. Hij komt met name in het nieuws door zijn toetreding tot de ''Académie Francaise'' in 1955 en de fresco’s die hij schildert in plaatsen aan de Côte d’Azur. | |||
<br/>Hoewel hij op hoge leeftijd is, komt zijn dood toch nog vrij onverwacht. In oktober 1963 serft hij in Milly-la-Forêt. Cocteau ligt begraven in het kleine kapelletje van Milly-la-Forêt, een dorpje nabij Fontainebleau. ''Je reste avec vous'' staat in guirlande-schrift op zijn graf geschreven. | |||
{{Bron|bronvermelding= | |||
*<sup> 1)</sup> De Ballets Russes was een balletgezelschap uit Rusland, gesticht door Sergej Djagilev. Tussen 1909 en 1929 traden de Ballets Russes op in tal van westerse landen.}} | |||
[[Categorie: Literatuur]] | |||
[[Categorie: Schilderkunst]] | |||
[[Categorie: Ballet]] | |||
[[Categorie: Toneel]] | |||
{{Infobox Bmoc}} | |||
{{Infobox Bmoc}} | |||
<br/> | |||
{{Infobox Bmoc}} | |||
| Regel 34: | Regel 277: | ||
| Regel 67: | Regel 288: | ||
| Regel 333: | Regel 311: | ||
| Regel 347: | Regel 317: | ||
||<sup>{{math|i{{=}}1}}</sup> | |||
|} | |||
{| | :{| | ||
| ||<sub> </sub> | |||
|- | |- | ||
|<big>{{Math|<big>''Ψ'' || {{math|('''''x⃗,t''''')|</big>}} | |||
'' | |||
|- | |- | ||
| | | ||<sup></sup> | ||
|} | |||
De stad Montfort-L'Amaury in eerbetoon aan Maurice Ravel die in dit huis van 1921 tot 1937 woonde | |||
Ravel se fixa à Montfort-l'Amaury en 1921. Sa maison, le Belvédère, conservée en l'état selon la volonté de son frère, abrite un musée depuis 1971 et fait l’objet d’une inscription auprès des monuments historiques depuis 199459. | |||
Français : Maison dite du Belvédère de Maurice Ravel à Montfort-l'Amaury (Yvelines, France) | |||
Date 20 November 2006 | |||
Source Cliché personnel, own work | |||
Author ℍenry Salomé (Jaser !) 08:17, 21 November 2006 (UTC) | |||
Object location | |||
48° 46′ 34.28″ N, 1° 48′ 19.4″ E Kartographer map based on OpenStreetMap. View this and other nearby images on: OpenStreetMap - Google Earth info | |||
Licensing[edit] | |||
The copyright holder of this work, hereby publish it under the following licenses: | |||
GNU head Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License. | |||
<span> | |||
<font> | |||
::<span style="font-size:150%;"><font color=red>OPVS FUNDATUM VATICANVM | |||
:<span style="font-size:150%;"><font color=black>Josephvs Ratzinger - Benedictvs XVI | |||
::<span style="font-size:110%;"><font color=black>- Cooperatores Veritatis - | |||
</font> | |||
<span> | |||
<span> | |||
<font> | |||
::<span style="font-size:150%;"><font color=red>OPUS FUNDUM VATICANUM | |||
:<span style="font-size:150%;"><font color=black>Josephus Ratzinger - Benedictus XVI | |||
::<span style="font-size:110%;"><font color=black>- Cooperatores Veritatis - | |||
</font> | |||
<span> | |||
{{infobox}} | |||
| | |||
<span> | |||
<font> | |||
:<span style="font-size:150%;"><font color=black>''Priemgetallen blijken niet zo willekeurig te zijn als men eerder had aangenomen.'' | |||
</font> | |||
<span> | |||
|} | |||
| Regel 389: | Regel 474: | ||
span> | |||
<font> | |||
:<span style="font-size:150%;"><font color=black>''Ook in de bioscoop werden antifascistische acties uitgevoerd'' | |||
</font> | |||
<span> | |||
|} | |||
Enkele breuken hebben een eigen naam: | |||
* {{vbreuk|2}} [[half]] | |||
* {{vbreuk|4}} [[kwart (breuk)|kwart]] | |||
* {{vbreuk|3|4}} [[driekwart]] | |||
* {{vbreuk|1|1|2}} [[anderhalf]] | |||
* '''√<sup>12</sup>''' | |||
≈12 | |||
{{vbreuk|1|1}} = 1 | |||
* | * <big>2<sup>{{vbreuk|0|12}}</sup> = 1</big> | ||
* <big>2<sup>{{vbreuk|1|12}}</sup> = 1,059463094</big> | |||
< | |||
< | |||
< | |||
</ | |||
</ | |||
* <big>2<sup>{{vbreuk|2|12}}</sup> = 1,122462048</big> | |||
{{vbreuk|x|4}} | |||
√{{vbreuk|L|C}} | |||
{{infobox}} | |||
| | |||
<span> | |||
<font> | |||
:<span style="font-size:150%;"><font color=blue>''Zijn eerste composities schreef Elgar voor amateurs.'' | |||
</font> | |||
<span> | |||
|} | |||
{{infobox}} | |||
| | |||
<span> | |||
<font> | |||
:<span style="font-size:150%;"><font color=blue> "''Heeft men een goed boek uitgelezen, dan is het alsof men van een goede vriend afscheid neemt.''" | |||
</font> | |||
<span> | |||
|} | |||
[[Categorie: Literatuur]] | |||
[[Categorie: Tijdschrift]] | |||
[[Categorie: Literair genre]]{{infobox}} | |||
| | |||
<font color=black> | |||
<span> | |||
<font> | |||
:<span style=font-size:150%;><font color=blue>''Het ballet veroorzaakte een enorm schandaal. '' | |||
</font> | |||
<span> | |||
|} | |||
[[Categorie: Vakliteratuur]] | |||
{{infobox}} | |||
| | |||
<span> | <span> | ||
<font> | <font> | ||
<span style="font-size:150%;"><font color= | :<span style="font-size:150%;"><font color=blue>''Priemgetallen blijken niet zo willekeurig te zijn als men eerder had aangenomen.'' | ||
</font> | |||
<span> | |||
|} | |||
{| class="wikitable" | |||
<span style="font-size:150%;"> | |||
<font color=black> | |||
! Op een gegeven moment stelt hij vast, | |||
dat het een verloren zaak is. | |||
</font> | </font> | ||
</span> | </span> | ||
< | |} | ||
< | |||
: | {{infobox}} | ||
| | |||
<font color=blue> | |||
<big> | |||
:''Een streamer bevat een zeer korte'' | |||
: | :''tekst van twee of drie regels.'' | ||
}} | </big> | ||
</font> | |||
|} | |||
<span style="font-size:150%;"> | |||
<font color=blue> | |||
::::*'''Het schrijven van de Magister Ludi aan de Pedagogische Dienst''' | |||
</font> | |||
</span> | |||
|} | |||
{{infobox}} | |||
| | |||
<font color=blue> | |||
:.....''dat hij al tekenen waarneemt, dat in de nabije toekomst '''Het Kralenspel''' | |||
: ''als eerste verloren zal gaan.'' | |||
</font> | |||
|} | |||
:<code><nowiki>{{Overline| (12)}}</nowiki></code> {{overline|om ergens een lijntje boven te trekken}} | |||
:<code><nowiki>{{Overline|24}}</nowiki></code> | |||
''12 | |||
''<br/> | |||
{{Overline|''24''}} | |||
12 | |||
<br/>-- | |||
<br/>24 | |||
==Breuken== | |||
<!--<math>\mathbb{Z}</math>--> [[Bestand:Zmath.png|9px]] | |||
<!--<math>\mathbb{R}</math>--> [[Bestand:Rmath.png|9px]] | |||
<!--<math>\mathbb{C}</math>--> [[Bestand:Cmath.png|9px]] | |||
Als dit in een zin staat <!--[[Blackboard bold|<math>\mathbb{N}</math>.]] --> [[Bestand:Nmath.png|10px]] | |||
{{Breuk|a|b|c}}: a b/c (geheel getal, teller en noemer) | |||
{{Breuk|a|b}}: a/b (teller en noemer) | |||
{{Breuk|a}}: 1/a (alleen noemer) | |||
12 | |||
<br/>-- | |||
<br/>24 | |||
:<code><nowiki>{{Overline|a}}</nowiki></code> | |||
''12'' | |||
<br/> | |||
{{Overline|''24''}} | |||
{{Overline|''a''}} | |||
| Regel 470: | Regel 642: | ||
:<code><nowiki>{{Overline|24}}</nowiki></code> | |||
''12'' | |||
<br/> | <br/> | ||
{{Overline|''24''}} | |||
{{I =vbreuk|U|R|}} | |||
<br/> | <br/> | ||
In deze theoretische verhandeling, wordt de vergelijking: | |||
'''''S''''' = {{vbreuk|'''''A'''''|'''''L'''''}} geïntroduceerd. | |||
<br/>Hierbij is: | |||
:*'''''S''''' de stroom | |||
:*'''''A''' de spanning | |||
:*'''''L''''' de weerstand | |||
Later zijn deze letters vervangen door de huidige notatie: | |||
'''''I''''' = {{vbreuk|'''''U'''''|'''''R'''''}} | |||
sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = sin 32,3122 0 = 0,5345 | |||
{{overline|24}} | |||
==Schrijfwijze== | |||
Het hoofdtelwoord geeft de [[teller (breuk)|teller]] van een [[breuk (wiskunde)|breuk]] weer, het rangtelwoord de [[noemer]]. | |||
* {{vbreuk|5}} een vijfde, {{vbreuk|7|10}} zeven tiende, {{vbreuk|1|2|6}} een twee zesde. | |||
* {{vbreuk|11|1|5}} elf en een vijfde, elf een vijfde, of elf gehelen en een vijfde. | |||
---------------------------------------------- | |||
Enkele breuken hebben een eigen naam: | |||
* {{vbreuk|2}} [[half]] | |||
* {{vbreuk|4}} [[kwart (breuk)|kwart]] | |||
* {{vbreuk|3|4}} [[driekwart]] | |||
* {{vbreuk|1|1|2}} [[anderhalf]] | |||
------------------------------------------------- | |||
Een ''derde'' lijkt een eigen naam te hebben. Het is als breuk een "gewone" combinatie (''derde'' is het rangtelwoord van drie): | |||
* {{vbreuk|3}} ''een'' derde (dus niet ''eenderde'') | |||
* {{vbreuk|2|3}} ''twee'' derde. | |||
---------------------------------------------------------------- | |||
{{vbreuk|sina|cosa}} | |||
* {{vbreuk|30-10|5}} | |||
{{vbreuk|60|24/60}} | |||
:<big>'''''R<sub>v</sub> = {{vbreuk|1|1R<sub>1</sub> + R<sub>2</sub> +......R<sub>n</sub>}}</big> | |||
{{vbreuk|5}} | |||
{{vbreuk|-|x}}(t) | |||
'' | |||
{{ | <big>'''''x<sup>→</sup>(t)''''' = '''''v<sup>→</sup> • t''''' + '''''x<sub>0'''''</sub><sup>→</sup> = {{vbreuk|'''''dx<sup>→</sup>|dt'''''}} • '''''t + x<sub>0</sub><sup>→'''''</sup></big> | ||
<big>{{vbreuk|''y(p)|x(p)''}} = {{vbreuk|''K • G(p)|1 + [K • G(p) • H(p)]''}}</big> | |||
sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = 0 = 0,5345 24 | |||
sin a = sin 32 + 18 + {{vbreuk|44|60/60}} = sin 32,3122 | |||
<big>Groter</big> | |||
{{infobox}} | |||
| | |||
<big> | |||
''Op een gegeven moment meent hij, dat hij de zin van het Spel dicht is genaderd, maar denkt toch dat hij dit niet tot zijn beroep moet maken.'' | |||
</big> | |||
|} | |||
23 • 60 • 60 = 82.800 | |||
128 <span style="font-size:125%;"><font color=black><sup> 4</sup>/<sub> 7</sub> <sup> 0</sup> </font></span> | 128 <span style="font-size:125%;"><font color=black><sup> 4</sup>/<sub> 7</sub> <sup> 0</sup> </font></span> | ||
| Regel 532: | Regel 727: | ||
::''Moon River, Goodnight Moon, Moon Cloud, Dark of the Moon'' | ::''Moon River, Goodnight Moon, Moon Cloud, Dark of the Moon'' | ||
| Regel 544: | Regel 733: | ||
{| | |||
|- | |||
|- | |||
|} | |||
| Regel 592: | Regel 785: | ||
[[Afbeelding:Paul Dukas.jpg|thumb|200px|right|]] | |||
| Regel 609: | Regel 803: | ||
: '''Δ BCD ~ Δ ABC''' | : '''Δ BCD ~ Δ ABC''' | ||
<br/>Franciscus 7 feb 2015 12:31 (CET) | <br/>Franciscus 7 feb 2015 12:31 (CET) | ||
Huidige versie van 9 okt 2019 om 19:23
Jean Cocteau

Jean Maurice Eugène Clément Cocteau (Maisons-Laffitte, 5 juli 1889 – Milly-la-Forêt, 11 oktober 1963) was een Frans dichter, romanschrijver, toneelschrijver, schilder, ontwerper en filmmaker. Cocteau heeft in zijn leven enorm veel geschreven en geproduceerd, en was thuis in bijna alle kunstvormen en was één van de belangrijkste personen binnen het surrealisme.
Zijn bekendste werken zijn het boek Les Enfants terribles (1929), het toneelstuk Les parents terribles en de film La Belle et la Bête (1946).
Cocteau is een tot de verbeelding sprekend kunstenaar. Maar meer nog dan om zijn werk was Cocteau bekend om zijn opmerkelijke leven. Hij omgaf zich met beroemdheden als Sergei Diaghilev van de Ballets Russes, de zangeres Edith Piaf en de schilder Pablo Picasso, en hij raakte geregeld in opspraak vanwege zijn homoseksualiteit en zijn drugsgebruik.
Afkomst en jeugd
Jean Cocteau, zoon van Georges en Eugénie Cocteau, werd op 5 juli 1889 geboren in Maisons-Laffitte, in het noordwesten van het stedelijk gebied van Parijs. Het echtpaar had al twee kinderen: Marthe, geboren in 1877 en Paul, geboren in in 1881.
Het gezin woonde in de winter samen met hun grootouders van moederszijde in een herenhuis in Parijs en in de zomer in Maisons-Laffitte.
Zijn familie was van een solide Parijse bourgeoisie: gecultiveerd, rijk en geïnteresseerd in muziek, schilderkunst en literatuur. Zijn vader - een jurist - tekent uit liefhebberij en op jonge leeftijd begint Jean dat ook te doen. Zijn grootvader is een muziekliefhebber die muzikale sessies in het huis organiseert.
|
|
Jean was een verwend maar nerveus kind. Hij had een grillig karakter en was vaak ziek.
De vroegste herinneringen van Cocteau hadden te maken met het theater in populaire vormen, zoals het circus en het ijspaleis, en met serieuze theaters, zoals de tragedies die werden uitgevoerd bij de Comédie-Française.
Op 5 april 1898 - als Jean 9 jaar oud is - pleegt zijn vader zelfmoord. De reden daarvoor is nooit opgehelderd. Het bleef een duister raadsel dat hem altijd blijft achtervolgen en grote invloed op Cocteau heeft uitgeoefend.
In het voorjaar sterft grootmoeder Lecomte. De grootvader blijft bij zijn dochter wonen. Hij zorgt voor Jean en neemt hem elke zondag mee naar concerten op het conservatorium. Op de Wereldtentoonstelling in Parijs van 1900 is Cocteau vol ontzag voor de dansvoorstellingen.
Na een periode van basisonderwijs - die in alle opzichten onder het gemiddelde lag en vaak werd onderbroken door slechte gezondheid - begint hij zijn eerste jaar op de middelbare school aan de Lycée Condorcet. Hij blinkt uit in slechts drie onderwerpen: tekenen, gymnastiek en Duits. Zijn leraren vinden hem intelligent, maar inconsistent, onoplettend en rusteloos.
Eerste publicaties
De toneelspeler Edouard Max introduceerde de 17-jarige Cocteau in de elitewereld van Parijs. Hij organiseerde een séance rond Cocteaus poëzie, waardoor hij in één keer naam maakte. Zonder hem had Cocteau vast nog een lange weg te gaan gehad door al leurende bij uitgevers aan te kloppen.
Cocteau wordt wel gezien als het product van de jaren onmiddellijk voorafgaand aan de Eerste Wereldoorlog; jaren van verfijnde artistieke smaak, zonder politieke onrust. Er heerste een idealistische en optimistische geest in Europa. Die periode werd ook wel de roaring twenties genoemd.
Zijn echte verkenning van de wereld van het theater begon, toen hij met de Ballets Russes 1) in aanraking kwam, geleid door Sergei Diaghilev. Toen Cocteau de wens uitsprak om balletten te maken, daagde Diaghilev hem uit met: "Etonne-moi" ("Verras me").In 1911 schreef hij het libretto voor Le dieu bleu, een ballet voor de Ballets Russes.
Eerste Wereldoorlog
Toen de Eerste Wereldoorlog bezig was, wilde Cocteau het leger in, maar werd afgekeurd. Hij wist een burgerkonvooi te organiseren om aan de frontlinie gewonden op te halen, waarbij hij als chauffeur fungeerde. Dat hield hij vol tot 1917.
Midden in de oorlog kwam Cocteau met Parade uit, een avant-gardeballet, waarvoor onder anderen Pablo Picasso de decorstukken en de kostuums ontwierp en Erik Satie de muziek componeerde. Cocteau en Picasso sloten zich aan bij de groep Ballets Russes van Sergei Diaghilev in Rome om het ballet voor te bereiden. De première van de Parade vond plaats op 18 mei 1917 in het Théâtre de Châtelet. Het publiek en de critici waren meer overbluft dan geërgerd door de muziek van Satie en de sets en kostuums van Picasso. De moderne muziek, het decor, het verhaal; alles was modern en het publiek wist er nog geen raad mee.
Op 12 juli van dat jaar zijn Jean Cocteau, de dichter en schrijver Guillaume Apollinaire en de dichter, schrijver en schilder Max Jacob, getuigen bij het huwelijk van Pablo Picasso en Olga Koklova.
Kritiek
Op een gegeven moment schetst Cocteau in 1919 zijn eigen specifieke kunstgevoel. Ondanks zijn inspanningen om betrokken te worden bij de publicatie van een belangrijk document daarover, wordt Cocteau buitengesloten. In die tijd ook publiceert de schrijver André Gide - een Nobelprijswinnaar - een open brief aan Jean Cocteau in de Nouvelle Revue française waarin hij de dichtbundel Le Cap de Bonne-Espérance (Kaap de Goede Hoop) en het ballet Parade bekritiseert. In hetzelfde artikel citeert Gide Le Coq et le Arlequin (De haan en de harlekijn) als bewijs dat de dichter geen muzikale vaardigheden bezit. Cocteau reageert hierop fel in het literaire tijdschrift Les Ecrits nouveaux , waarop Gide natuurlijk terugschiet. Voor Cocteau sluit deze vervelende polemiek tijdelijk de deur naar de Nouvelle Revue française , waarvoor hij bijdragen leverde.
Productie
In 1920 ontmoet hij de zestienjarige Raymond Radiguet, wat uitgroeit tot een liefdesverhouding. In datzelfde jaar wordt Cocteau de verdediger en grote inspirator van jonge musici, die al snel bekendheid verwerven als de "Groupe de Six".
Hij brengt juni en het grootste deel van juli door in Londen met Darius Milhaud om de Engelse productie van Le Bœuf sur le toit in het London Coliseum te verfijnen.
In oktober komt Cocteau uit met het boek Thomas l'imposteur (Thomas de bedrieger), waar in 1964 ook een film van is gemaakt.
Op 12 december sterft Radiguet bij gebrek aan onvoldoende medische begeleiding aan tyfus. De totaal ingestorte Cocteau woont de begrafenis niet bij.
Enige tijd later nemen Serge Diaghilev, Auric en Poulenc een radeloze Cocteau mee naar Monte-Carlo. Ze geven hem de raad om troost te zoeken in de opium, wat bij Cocteau tot verslaving leidt. Intussen werkt hij aan plannen voor het ballet Le Train bleu.
In 1925, ondergaat Cocteau - op aandringen van vrienden - een behandeling voor zijn opiumverslaving in de Clinique des Thermes Urbains.
|
|
Een periode van intense creativiteit volgt waarin veel werk van hem wordt gepubliceerd. In het jaar daarna schrijft hij het libretto voor de opera-oratorium Oedipus Rex voor Stravinsky die vanaf half januari aan de muziek werkt. In mei 1927 was de première, waarbij het werk niet onverdeeld gunstig werd ontvangen. In december vond in de Galerie des Quatre Chemins een tentoonstelling van ongewone objecten en tekeningen plaats met de titel Poésie plastique (Gebeeldhouwde poëzie). Het was een eerste pogingen van Cocteau tot creatie van een moderne post-kubistische kunst in Frankrijk Op 16 december 1927 première van de opera Pauvre matelot (The Poor Sailor), met muziek van Darius Milhaud. Cocteau voltooit La voix humaine (The Human Voice) en schrijft Le Livre blanc (The White Book). Op 28 december gaat de opera Antigone in première in het Théâtre de la Monnaie in Brussel met muziek van Arthur Honneger. Eind november 1928 checkt hij in bij een kliniek in Saint-Cloud in voor een nieuwe poging tot afkicken. 1929 Maakt tekeningen, begint aan het boek Opium, journal d'une désintoxication en schrijft in drie weken Les Enfants terribles (Children of the Game), dat zeer gunstig wordt ontvangen. In het boek Opium beschrijft Cocteau's het herstel van zijn verslaving aan opium. Eind augustus 1931 blijkt hij besmet te zijn met tyfus en moet hij veertig dagen in een kliniek doorbrengen. Kort daarop begon hij weer met opium te roken. In 1933 ondergaat hij weer een kuur om daar van af te raken. Terwijl ze audities houden voor Oedipus Rex, merkt Cocteau Jean Marais op, en geeft hem een rol in het koor.
Cineast
Cocteau debuteerde pas op de relatief late leeftijd van 41 jaar als cineast. Cinema was destijds nog relatief jong, maar de regels van het medium leken al vast te liggen. Cocteau ging echter dapper en volstrekt autodidact zijn eigen koers, en heeft vervolgens een klein maar interessant oeuvre bij elkaar gefilmd. Zijn films worden tegenwoordig nog steeds bekeken en gewaardeerd vanwege hun unieke stijl en sfeer. La Belle et la Bête, Orphée en andere films waren succesvol De film Orphée uit 1950 wordt algemeen beschouwd als zijn meesterwerk. Het is een zichzelf mythologiserend portret van de gekwelde kunstenaar, die te kampen heeft met innerlijke demonen, zijn schrijverschap, liefde, dood en de confrontatie met zijn publiek.
Laatste jaren
Tijdens de herfst van zijn leven leidt Cocteau een betrekkelijk rustig bestaan. Hij komt met name in het nieuws door zijn toetreding tot de Académie Francaise in 1955 en de fresco’s die hij schildert in plaatsen aan de Côte d’Azur.
Hoewel hij op hoge leeftijd is, komt zijn dood toch nog vrij onverwacht. In oktober 1963 serft hij in Milly-la-Forêt. Cocteau ligt begraven in het kleine kapelletje van Milly-la-Forêt, een dorpje nabij Fontainebleau. Je reste avec vous staat in guirlande-schrift op zijn graf geschreven.
Bronvermelding
Bronnen, noten en/of referenties:
- 1) De Ballets Russes was een balletgezelschap uit Rusland, gesticht door Sergej Djagilev. Tussen 1909 en 1929 traden de Ballets Russes op in tal van westerse landen.
| Dit is een artikel uit de serie: Bekende melodie, onbekende componist |
|---|
| Dit is een artikel uit de serie: Bekende melodie, onbekende componist |
|---|
| Dit is een artikel uit de serie: Bekende melodie, onbekende componist |
|---|
||i=1 |}
Ψ (x⃗,t)
De stad Montfort-L'Amaury in eerbetoon aan Maurice Ravel die in dit huis van 1921 tot 1937 woonde Ravel se fixa à Montfort-l'Amaury en 1921. Sa maison, le Belvédère, conservée en l'état selon la volonté de son frère, abrite un musée depuis 1971 et fait l’objet d’une inscription auprès des monuments historiques depuis 199459. Français : Maison dite du Belvédère de Maurice Ravel à Montfort-l'Amaury (Yvelines, France) Date 20 November 2006 Source Cliché personnel, own work Author ℍenry Salomé (Jaser !) 08:17, 21 November 2006 (UTC) Object location 48° 46′ 34.28″ N, 1° 48′ 19.4″ E Kartographer map based on OpenStreetMap. View this and other nearby images on: OpenStreetMap - Google Earth info Licensing[edit] The copyright holder of this work, hereby publish it under the following licenses: GNU head Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.
- OPVS FUNDATUM VATICANVM
- Josephvs Ratzinger - Benedictvs XVI
- - Cooperatores Veritatis -
- OPUS FUNDUM VATICANUM
- Josephus Ratzinger - Benedictus XVI
- - Cooperatores Veritatis -
|
|
span>
- Ook in de bioscoop werden antifascistische acties uitgevoerd
|}
Enkele breuken hebben een eigen naam:
- √12
≈12 1 1 = 1
- 2 0 12 = 1
- 2 1 12 = 1,059463094
- 2 2 12 = 1,122462048
x 4
√ L C
|
|
|
|
|
|
|
|
| Op een gegeven moment stelt hij vast,
dat het een verloren zaak is. |
|---|
|
|
- Het schrijven van de Magister Ludi aan de Pedagogische Dienst
|}
|
|
{{Overline| (12)}}om ergens een lijntje boven te trekken{{Overline|24}}
12
24
12
--
24
Breuken
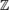
Bestand:Rmath.png

a b⁄c: a b/c (geheel getal, teller en noemer)
a⁄b: a/b (teller en noemer)
1⁄a: 1/a (alleen noemer)
12
--
24
{{Overline|a}}
12
24
a
{{Overline|24}}
12
24
Sjabloon:I =vbreuk
In deze theoretische verhandeling, wordt de vergelijking:
S = A L geïntroduceerd.
Hierbij is:
- S de stroom
- A de spanning
- L de weerstand
Later zijn deze letters vervangen door de huidige notatie: I = U R
sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = sin 32,3122 0 = 0,5345 24
Schrijfwijze
Het hoofdtelwoord geeft de teller van een breuk weer, het rangtelwoord de noemer.
- 1 5 een vijfde, 7 10 zeven tiende, 1 2 6 een twee zesde.
- 11 1 5 elf en een vijfde, elf een vijfde, of elf gehelen en een vijfde.
Enkele breuken hebben een eigen naam:
Een derde lijkt een eigen naam te hebben. Het is als breuk een "gewone" combinatie (derde is het rangtelwoord van drie):
- 1 3 een derde (dus niet eenderde)
- 2 3 twee derde.
sina cosa
- 30-10 5
60 24/60
- Rv = 1 1R1 + R2 +......Rn
1 5
- x(t)
x→(t) = v→ • t + x0→ = dx→ dt • t + x0→
y(p) x(p) = K • G(p) 1 + [K • G(p) • H(p)]
sin α = sin 32 0 + 18 + [ ( 44 ) / 60 ) / 60 ] = 0 = 0,5345 24
sin a = sin 32 + 18 + 44 60/60 = sin 32,3122
Groter
|
Op een gegeven moment meent hij, dat hij de zin van het Spel dicht is genaderd, maar denkt toch dat hij dit niet tot zijn beroep moet maken. |
23 • 60 • 60 = 82.800
128 4/ 7 0 achtenveertig achtenveertig
- P = U • I • cos φ
- P = 3U f • I f • cos φ
waarbij:
- U f = U fase en I f = I fase
- P = 3 U fase• I fase • cos φ
- Moon River, Goodnight Moon, Moon Cloud, Dark of the Moon

- Δ BCD ~ Δ ABC
Franciscus 7 feb 2015 12:31 (CET)
