Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Rekenliniaal: verschil tussen versies
Geen bewerkingssamenvatting |
|||
| (4 tussenliggende versies door 2 gebruikers niet weergegeven) | |||
| Regel 1: | Regel 1: | ||
Een '''rekenliniaal''' is een analoog, [[Wiskunde|wiskundig]] instrument waarmee tot ongeveer 1980 op kleine schaal allerlei berekeningen werden uitgevoerd. Het was hét instrument voor technische en economische toepassingen, voor opleidingen en voor gebruik op ontwerpbureaus. | Een '''rekenliniaal''' is een analoog, [[Wiskunde|wiskundig]] instrument waarmee tot ongeveer 1980 op kleine schaal allerlei berekeningen werden uitgevoerd. Het was hét instrument voor technische en economische toepassingen, voor opleidingen en voor gebruik op ontwerpbureaus. | ||
Toen eenmaal de handzame, elektronische zakrekenmachines op de markt kwamen, was de rekenliniaal – die zo’n 400 jaar geleden zijn intrede deed - tamelijk snel verdwenen. | |||
Toch is er nog steeds belangstelling voor dit instrument. Zo bestaat er bijvoorbeeld '''De Nederlandse Kring van Verzamelaars van Rekenlinialen''', en zijn er meer dan 1000 verzamelaars van rekenlinialen bekend over de hele wereld. | Toch is er nog steeds belangstelling voor dit instrument. Zo bestaat er bijvoorbeeld '''De Nederlandse Kring van Verzamelaars van Rekenlinialen''', en zijn er meer dan 1000 verzamelaars van rekenlinialen bekend over de hele wereld. | ||
[[Afbeelding:Rekenliniaal.jpg|thumb|800px|left|Rekenliniaal van kunststof]] | [[Afbeelding:Rekenliniaal.jpg|thumb|800px|left|Rekenliniaal van kunststof]] | ||
==Principe van de rekenliniaal== | ==Principe van de rekenliniaal== | ||
Het principe van de rekenliniaal is gebaseerd op het logaritmische stelsel van de Engelse wiskundigen | Het principe van de rekenliniaal is gebaseerd op het logaritmische stelsel van de Engelse wiskundigen [[John Napier]] en [[Henry Briggs]], waarbij het getal '''10''' het '''grondtal''' is. | ||
Tussen '''10 <sup> 0</sup>''' en '''10 <sup>1</sup>''' of | Tussen '''10<sup>0</sup>''' en '''10<sup>1</sup>''' of bijvoorbeeld tussen '''10<sup>1</sup>''' en '''10<sup>2</sup>''' liggen namelijk exponenten van '''10''' die een ander getal dan '''1, 10''' of '''100''' opleveren. | ||
<br/>Als bijvoorbeeld de wortel uit '''10''' wordt genomen, dan wordt deze aldus genoteerd: | <br/>Als bijvoorbeeld de wortel uit '''10''' wordt genomen, dan wordt deze aldus genoteerd: | ||
<table width="100%" border="1"> | <table width="100%" border="1"> | ||
<tr> | <tr> | ||
<td align="center" bgcolor=#fff7cb> | <td align="center" bgcolor=#fff7cb> | ||
'''√ 10 = 3,1622'''. | '''√{{overline| 10 }} = 3,1622'''. | ||
<br/> | <br/> | ||
'''Een andere schrijfwijze voor de wortel uit 10 is 10 <sup> | '''Een andere schrijfwijze voor de wortel uit 10 is 10<sup>½</sup> = 10<sup>0,5</sup> wat hetzelfde oplevert, namelijk 3,1622'''. | ||
<br/>'''Op dezelfde manier kan elk getal worden uitgedrukt met het getal 10 met een exponent'''. | <br/>'''Op dezelfde manier kan elk getal worden uitgedrukt met het getal 10 met een exponent'''. | ||
<br/>'''Zo levert de exponent 0,3010 het getal 2 op, aldus 10<sup> 0,30101</sup> = 2, of bijvoorbeeld 10<sup> 0, | <br/>'''Zo levert de exponent 0,3010 het getal 2 op, aldus 10<sup>0,30101</sup> = 2, of bijvoorbeeld 10<sup>0,6990</sup> = 5'''. | ||
<br/>'''De exponent van het grondtal 10 wordt ''mantisse'' genoemd.''' | <br/>'''De exponent van het grondtal 10 wordt ''mantisse'' genoemd.''' | ||
<br/> '''Als een getal > 10 maar < 100 is, dan wordt vóór de mantisse het cijfer 1 geplaatst.''' | <br/> '''Als een getal > 10 maar < 100 is, dan wordt vóór de mantisse het cijfer 1 geplaatst.''' | ||
<br/> '''Als een getal > 100 maar < 1000 is, dan wordt vóór de mantisse het cijfer 2 geplaatst, enz. | <br/> '''Als een getal > 100 maar < 1000 is, dan wordt vóór de mantisse het cijfer 2 geplaatst, enz.''' | ||
''' | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Om elk getal in een exponent uit te kunnen drukken, zijn voor alle getallen tussen '''1''' en '''99''' tabellen opgesteld, die deze notering mogelijk maken. In deze tabellen zijn de exponenten | Om elk getal in een exponent uit te kunnen drukken, zijn voor alle getallen tussen '''1''' en '''99''' tabellen opgesteld, die deze notering mogelijk maken. In deze tabellen zijn de exponenten, die hier '''mantissen van de Briggse logaritmen''' worden genoemd, opgenomen. | ||
{| class=prettytable | |||
!colspan=11 |'''''Tabel van mantissen''''' | |||
|- | |- | ||
! Getal | ! Getal !! 0 !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7 !! 8 !! 9 | ||
! 0 | |||
! 1 | |||
! 2 | |||
! 3 | |||
! 4 | |||
! 5 | |||
! 6 | |||
! 7 | |||
! 8 | |||
! 9 | |||
|- | |- | ||
|''' 0 ''' || | |<center>'''0'''</center>|| <span style="font-size:150%;">− '''∞'''</span> ||'''0000'''||<font color=red>'''3010'''</font>||'''4771'''||'''6021'''||'''6990''' |||<font color=red>'''7782'''</font>||'''8451'''|| '''9031''' ||'''9542''' | ||
<span style="font-size:150%;"> | |||
</span> | |||
||'''0000'''|| | |||
<font color=red> | |||
'''3010''' | |||
</font> | |||
||'''4771'''||'''6021'''||''' | |||
<font color=red> | |||
'''7782''' | |||
</font> | |||
||'''8451'''|| '''9031''' ||''' 9542''' | |||
|- | |- | ||
|''' 1''' ||'''0000''' || '''0414''' || | |<center>'''1'''</center>||'''0000''' || '''0414''' ||<font color=red>'''0792'''</font>|| '''1139''' || '''1461''' || '''1761''' || '''2041''' || '''2304''' ||'''2553''' ||'''2788''' | ||
<font color=red> | |||
'''0792''' | |||
</font> | |||
|| '''1139''' || '''1461''' || '''1761''' || '''2041''' || '''2304''' ||''' 2553''' ||'''2788''' | |||
|- | |- | ||
| '''2''' || '''3010''' ||''' 3222''' || '''3424''' ||''' 3617''' || '''3802''' || '''3979''' || '''4150''' || '''4314''' || '''4472''' ||''' 4624''' | |<center>'''2'''</center>|| '''3010''' ||'''3222''' || '''3424''' ||'''3617''' || '''3802''' || '''3979''' || '''4150''' || '''4314''' || '''4472''' ||'''4624''' | ||
|- | |- | ||
| '''3''' ||''' 4771''' || '''4914''' || '''5051''' || '''5185''' || '''5315''' || '''5441''' || '''5563''' ||''' 5682''' || '''5798''' ||''' 5911''' | |<center>'''3'''</center>||''' 4771''' || '''4914''' || '''5051''' || '''5185''' || '''5315''' || '''5441''' || '''5563''' ||'''5682''' || '''5798''' ||'''5911''' | ||
|- | |- | ||
|''' 4''' || '''6021''' ||'''6128''' ||'''6232'''|| '''6335''' ||'''6435'''||'''6532'''||'''6628'''||'''6721'''||'''6812'''||'''6902''' | |<center>'''4'''</center>|| '''6021''' ||'''6128''' ||'''6232'''|| '''6335''' ||'''6435'''||'''6532'''||'''6628'''||'''6721'''||'''6812'''||'''6902''' | ||
|- | |- | ||
|''' 5''' ||'''6990'''||'''7076'''||'''7160'''||'''7243'''||'''7324'''||'''7404'''||'''7482'''||'''7559'''||'''7634'''||'''7709''' | |<center>'''5'''</center>||'''6990'''||'''7076'''||'''7160'''||'''7243'''||'''7324'''||'''7404'''||'''7482'''||'''7559'''||'''7634'''||'''7709''' | ||
|- | |- | ||
||'''enz → t/m 99''' | ||'''enz → t/m 99''' || || || || || || || || || || | ||
|} | |} | ||
Getallen > '''99''' kunnen door ''interpolatie'' ook uit deze tabellen worden samengesteld. | Getallen > '''99''' kunnen door ''interpolatie'' ook uit deze tabellen worden samengesteld. | ||
==Werkwijze== | ==Werkwijze== | ||
[[Afbeelding:Logaritmische verdeling .jpg|thumb|500px|right|Logaritmische verdeling]] | [[Afbeelding:Logaritmische verdeling .jpg|thumb|500px|right|Logaritmische verdeling]] | ||
Als twee linialen met een identieke logaritmische schaalverdeling langs elkaar worden geschoven, dan kunnen – volgens de [[Logaritmen en exponentiële functies|logaritmische]] principes de gevonden waarden als logaritme worden ''opgeteld'' of worden ''afgetrokken'', wat overeenkomt met ''vermenigvuldigen'' of met ''delen''. Bij het werken met logaritmen geldt namelijk, dat: | Als twee linialen met een identieke logaritmische schaalverdeling langs elkaar worden geschoven, dan kunnen – volgens de [[Logaritmen en exponentiële functies|logaritmische]] principes de gevonden waarden als logaritme worden ''opgeteld'' of worden ''afgetrokken'', wat overeenkomt met ''vermenigvuldigen'' of met ''delen''. Bij het werken met logaritmen geldt namelijk, dat: | ||
<br/> | <br/> | ||
:* '''log a | :* '''log a ⋅ b = log a + log b''' | ||
bij een vermenigvuldiging, en: | bij een vermenigvuldiging, en: | ||
<br/> | <br/> | ||
:* '''log a : b = log a – log b ''' | :* '''log a : b = log a – log b ''' | ||
bij een deling. | bij een deling. | ||
<br/>Op de schalen van de rekenliniaal worden de logaritmen van de getallen lineair afgebeeld: daardoor is het lijnstuk tussen de getallen '''1''' en '''2''' '''( = 0,3010 | <br/>Op de schalen van de rekenliniaal worden de logaritmen van de getallen lineair afgebeeld: daardoor is het lijnstuk tussen de getallen '''1''' en '''2''' '''( = 0,3010 − 0,000 )''' even lang als het lijnstuk tussen '''2''' en '''4''' '''( = 0,6021 − 0,3010 )''', dat op zijn beurt weer even lang is als de afstand tussen '''4''' en '''8 ( = 0,9031 − 0,6021 ).''' | ||
<br/>Als bijvoorbeeld het getal '''2''' wordt vermenigvuldigd met '''6''' | <br/>Als bijvoorbeeld het getal '''2''' wordt vermenigvuldigd met '''6''', ''zoals weergegeven in de eerste afbeelding'', dan gebeurt het volgende: | ||
Op de afbeelding staat het cijfer '''1''' op de schuif tegenover het cijfer '''2''' van het lichaam. Als de | Op de bovenste afbeelding staat het cijfer '''1''' op de schuif tegenover het cijfer '''2''' van het lichaam. Als de loper naar rechts wordt geschoven totdat de zwarte markering op '''6''' staat, dam wordt op de schaal van het lichaam de uitkomst '''12''' afgelezen. | ||
<br/> Hier is dus het volgende gebeurd: | <br/> Hier is dus het volgende gebeurd: | ||
<br/> | <br/> | ||
:* '''log 2 | :* '''log 2 ⋅ 6 = log 2 + log 6 = 0,3010 + 0,7782 = 1,0792 → 10<sup>1,0792</sup> = 12''' | ||
Het getal '''12''' is | Het getal '''12''' is – in logaritmische verhouding – aanwezig op de schaalverdeling van het lichaam. | ||
<br/>Zou het getal '''20''' moeten worden vermenigvuldigd met '''6''', dan wordt dezelfde bewerking uitgevoerd. Aangezien bij het getal''' 20''' een '''1''' voor de mantisse hoort te staan, wordt het getal '''12''' nu dus '''120''' . | <br/>Zou het getal '''20''' moeten worden vermenigvuldigd met '''6''', dan wordt dezelfde bewerking uitgevoerd. Aangezien bij het getal '''20''' een '''1''' voor de mantisse hoort te staan, wordt het getal '''12''' nu dus '''120''' . | ||
<br/>Het is duidelijk, dat bij het werken met de rekenliniaal af en toe geschat moet worden welke orde van grootte kan worden verwacht. | <br/>Het is duidelijk, dat bij het werken met de rekenliniaal af en toe geschat moet worden welke orde van grootte kan worden verwacht. | ||
==Onderverdelingen en uitvoeringen== | ==Onderverdelingen en uitvoeringen== | ||
:* De bovenste schaal loopt meestal van '''10<sup> 0</sup> = 1''' tot '''10<sup> 2</sup> = 100'''. De onderste schaal is wat fijner verdeeld en loopt als regel van ''' 10<sup> 0</sup> = 1''' tot '''10<sup> 1</sup> = 10.''' | :* De bovenste schaal loopt meestal van '''10<sup>0</sup> = 1''' tot '''10<sup>2</sup> = 100'''. De onderste schaal is wat fijner verdeeld en loopt als regel van '''10<sup>0</sup> = 1''' tot '''10<sup>1</sup> = 10.''' | ||
:* De bovenste schaal laat het '''kwadraat''' zien van het tegenoverliggende getal op de onderste schaal. | :* De bovenste schaal laat het '''kwadraat''' zien van het tegenoverliggende getal op de onderste schaal. | ||
:* Bij de meeste rekenlinialen kan de loper er worden uitgenomen en totaal worden omgedraaid, waardoor met ''goniometrische functies'' kan worden gewerkt. | :* Bij de meeste rekenlinialen kan de loper er worden uitgenomen en totaal worden omgedraaid, waardoor met ''goniometrische functies'' kan worden gewerkt. | ||
:* Voor allerlei vakgebieden, als elektrotechniek, werktuigbouw en bouwkunde zijn rekenlinialen ontwikkeld met vaste, veelgebruikte en specifieke kenmerken die bij elk vakgebied horen. | :* Voor allerlei vakgebieden, als elektrotechniek, werktuigbouw en bouwkunde zijn rekenlinialen ontwikkeld met vaste, veelgebruikte en specifieke kenmerken die bij elk vakgebied horen. | ||
:* Aan de bovenzijde van de rekenliniaal wordt | :* Aan de bovenzijde van de rekenliniaal wordt, afhankelijk van de lengte, bijna altijd een verdeling in millimeters aangebracht, zodat het instrument ook als ''gewone liniaal'' kan dienst doen. | ||
:*Er zijn ook rekenlinialen die als '''schijf''' zijn uitgevoerd, en worden dan ''' | :*Er zijn ook rekenlinialen die als '''schijf''' zijn uitgevoerd, en worden dan '''rekenschijf''' genoemd. In principe is de werkwijze gelijk aan die van de gewone rekenliniaal. | ||
:* Die eerste rekenlinialen werden uitgevoerd in hout, maar in de loop der tijd werden diverse andere materialen gebruikt. Later gebruikte men ook metaal. Uitgangspunt was steeds een materiaal te kiezen, dat weinig rek of krimp vertoont. Naast perenhout, beukenhout of mahoniehout, werden ook andere materialen gebruikt, zoals een combinatie van hout of bamboe met bakeliet of andere kunststoffen. De laatste jaren werden rekenlinialen veelal alleen nog maar van kunststof gemaakt. | :* Die eerste rekenlinialen werden uitgevoerd in hout, maar in de loop der tijd werden diverse andere materialen gebruikt. Later gebruikte men ook metaal. Uitgangspunt was steeds een materiaal te kiezen, dat weinig rek of krimp vertoont. Naast perenhout, beukenhout of mahoniehout, werden ook andere materialen gebruikt, zoals een combinatie van hout of bamboe met bakeliet of andere kunststoffen. De laatste jaren werden rekenlinialen veelal alleen nog maar van kunststof gemaakt. | ||
:* De rekenlinialen werden altijd | :* De rekenlinialen werden altijd – zoals dat bij instrumenten hoort – in lederen etuis geleverd. | ||
== Externe links == | == Externe links == | ||
| Regel 111: | Regel 78: | ||
* [http://sliderulemuseum.com International Slide Rule Museum] | * [http://sliderulemuseum.com International Slide Rule Museum] | ||
==Trivia== | ==Trivia== | ||
:* Hoewel het elektronische tijdperk al was aangebroken, werd in 1969 | :* Hoewel het elektronische tijdperk al was aangebroken, werd in 1969, toen de '''Apollo 11''' naar de maan werd gelanceerd, nog met de rekenliniaal gewerkt. In die tijd gebruikte men in vliegtuigen ook nog steeds speciale rekenlinialen. | ||
:* In de televisieserie '''Star Trek Enterprise''' uit de jaren | :* In de televisieserie '''Star Trek Enterprise''' uit de jaren ’70 van de vorige eeuw, gebruikt de wetenschapsofficier Mr. Spock een rekenschijf voor luchtvaartdoeleinden, wat natuurlijk een anachronisme is. Het tegenstrijdige daarvan is namelijk, dat de serie zich afspeelt in de 23e en 24e eeuw, met uiterst geavanceerde technologieën, waarbij blijkbaar nog niet aan een elektronische zakrekenmachine werd gedacht. | ||
::''Op de externe link : [http://sliderulemuseum.com International Slide Rule Museum] is een afbeelding opgenomen | ::''Op de externe link : [http://sliderulemuseum.com International Slide Rule Museum] is een afbeelding opgenomen van Mr. Spock met een rekenschijf''. | ||
:* {{Wikidata|Q190667}} | :* {{Wikidata|Q190667}} | ||
{{Commonscat|Slide rule}} | {{Commonscat|Slide rule}} | ||
[[Categorie: Wiskunde]] | [[Categorie: Wiskunde]] | ||
[[Categorie: Rekenen]] | [[Categorie: Rekenen]] | ||
[[Categorie:Rekenhulpmiddel]] | [[Categorie: Rekenhulpmiddel]] | ||
[[Categorie:Meetinstrument]] | [[Categorie: Meetinstrument]] | ||
[[Categorie:Geschiedenis van de computer]] | [[Categorie: Geschiedenis van de computer]] | ||
{{bloei}} | |||
Huidige versie van 7 nov 2023 om 00:49
Een rekenliniaal is een analoog, wiskundig instrument waarmee tot ongeveer 1980 op kleine schaal allerlei berekeningen werden uitgevoerd. Het was hét instrument voor technische en economische toepassingen, voor opleidingen en voor gebruik op ontwerpbureaus.
Toen eenmaal de handzame, elektronische zakrekenmachines op de markt kwamen, was de rekenliniaal – die zo’n 400 jaar geleden zijn intrede deed - tamelijk snel verdwenen. Toch is er nog steeds belangstelling voor dit instrument. Zo bestaat er bijvoorbeeld De Nederlandse Kring van Verzamelaars van Rekenlinialen, en zijn er meer dan 1000 verzamelaars van rekenlinialen bekend over de hele wereld.

Principe van de rekenliniaal
Het principe van de rekenliniaal is gebaseerd op het logaritmische stelsel van de Engelse wiskundigen John Napier en Henry Briggs, waarbij het getal 10 het grondtal is.
Tussen 100 en 101 of bijvoorbeeld tussen 101 en 102 liggen namelijk exponenten van 10 die een ander getal dan 1, 10 of 100 opleveren.
Als bijvoorbeeld de wortel uit 10 wordt genomen, dan wordt deze aldus genoteerd:
|
√ 10 = 3,1622.
|
Om elk getal in een exponent uit te kunnen drukken, zijn voor alle getallen tussen 1 en 99 tabellen opgesteld, die deze notering mogelijk maken. In deze tabellen zijn de exponenten, die hier mantissen van de Briggse logaritmen worden genoemd, opgenomen.
| Tabel van mantissen | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Getal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| − ∞ | 0000 | 3010 | 4771 | 6021 | 6990 | 7782 | 8451 | 9031 | 9542 | |
| 0000 | 0414 | 0792 | 1139 | 1461 | 1761 | 2041 | 2304 | 2553 | 2788 | |
| 3010 | 3222 | 3424 | 3617 | 3802 | 3979 | 4150 | 4314 | 4472 | 4624 | |
| 4771 | 4914 | 5051 | 5185 | 5315 | 5441 | 5563 | 5682 | 5798 | 5911 | |
| 6021 | 6128 | 6232 | 6335 | 6435 | 6532 | 6628 | 6721 | 6812 | 6902 | |
| 6990 | 7076 | 7160 | 7243 | 7324 | 7404 | 7482 | 7559 | 7634 | 7709 | |
| enz → t/m 99 | ||||||||||
Getallen > 99 kunnen door interpolatie ook uit deze tabellen worden samengesteld.
Werkwijze
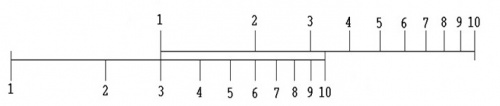
Als twee linialen met een identieke logaritmische schaalverdeling langs elkaar worden geschoven, dan kunnen – volgens de logaritmische principes de gevonden waarden als logaritme worden opgeteld of worden afgetrokken, wat overeenkomt met vermenigvuldigen of met delen. Bij het werken met logaritmen geldt namelijk, dat:
- log a ⋅ b = log a + log b
bij een vermenigvuldiging, en:
- log a : b = log a – log b
bij een deling.
Op de schalen van de rekenliniaal worden de logaritmen van de getallen lineair afgebeeld: daardoor is het lijnstuk tussen de getallen 1 en 2 ( = 0,3010 − 0,000 ) even lang als het lijnstuk tussen 2 en 4 ( = 0,6021 − 0,3010 ), dat op zijn beurt weer even lang is als de afstand tussen 4 en 8 ( = 0,9031 − 0,6021 ).
Als bijvoorbeeld het getal 2 wordt vermenigvuldigd met 6, zoals weergegeven in de eerste afbeelding, dan gebeurt het volgende:
Op de bovenste afbeelding staat het cijfer 1 op de schuif tegenover het cijfer 2 van het lichaam. Als de loper naar rechts wordt geschoven totdat de zwarte markering op 6 staat, dam wordt op de schaal van het lichaam de uitkomst 12 afgelezen.
Hier is dus het volgende gebeurd:
- log 2 ⋅ 6 = log 2 + log 6 = 0,3010 + 0,7782 = 1,0792 → 101,0792 = 12
Het getal 12 is – in logaritmische verhouding – aanwezig op de schaalverdeling van het lichaam.
Zou het getal 20 moeten worden vermenigvuldigd met 6, dan wordt dezelfde bewerking uitgevoerd. Aangezien bij het getal 20 een 1 voor de mantisse hoort te staan, wordt het getal 12 nu dus 120 .
Het is duidelijk, dat bij het werken met de rekenliniaal af en toe geschat moet worden welke orde van grootte kan worden verwacht.
Onderverdelingen en uitvoeringen
- De bovenste schaal loopt meestal van 100 = 1 tot 102 = 100. De onderste schaal is wat fijner verdeeld en loopt als regel van 100 = 1 tot 101 = 10.
- De bovenste schaal laat het kwadraat zien van het tegenoverliggende getal op de onderste schaal.
- Bij de meeste rekenlinialen kan de loper er worden uitgenomen en totaal worden omgedraaid, waardoor met goniometrische functies kan worden gewerkt.
- Voor allerlei vakgebieden, als elektrotechniek, werktuigbouw en bouwkunde zijn rekenlinialen ontwikkeld met vaste, veelgebruikte en specifieke kenmerken die bij elk vakgebied horen.
- Aan de bovenzijde van de rekenliniaal wordt, afhankelijk van de lengte, bijna altijd een verdeling in millimeters aangebracht, zodat het instrument ook als gewone liniaal kan dienst doen.
- Er zijn ook rekenlinialen die als schijf zijn uitgevoerd, en worden dan rekenschijf genoemd. In principe is de werkwijze gelijk aan die van de gewone rekenliniaal.
- Die eerste rekenlinialen werden uitgevoerd in hout, maar in de loop der tijd werden diverse andere materialen gebruikt. Later gebruikte men ook metaal. Uitgangspunt was steeds een materiaal te kiezen, dat weinig rek of krimp vertoont. Naast perenhout, beukenhout of mahoniehout, werden ook andere materialen gebruikt, zoals een combinatie van hout of bamboe met bakeliet of andere kunststoffen. De laatste jaren werden rekenlinialen veelal alleen nog maar van kunststof gemaakt.
- De rekenlinialen werden altijd – zoals dat bij instrumenten hoort – in lederen etuis geleverd.
Externe links
Trivia
- Hoewel het elektronische tijdperk al was aangebroken, werd in 1969, toen de Apollo 11 naar de maan werd gelanceerd, nog met de rekenliniaal gewerkt. In die tijd gebruikte men in vliegtuigen ook nog steeds speciale rekenlinialen.
- In de televisieserie Star Trek Enterprise uit de jaren ’70 van de vorige eeuw, gebruikt de wetenschapsofficier Mr. Spock een rekenschijf voor luchtvaartdoeleinden, wat natuurlijk een anachronisme is. Het tegenstrijdige daarvan is namelijk, dat de serie zich afspeelt in de 23e en 24e eeuw, met uiterst geavanceerde technologieën, waarbij blijkbaar nog niet aan een elektronische zakrekenmachine werd gedacht.
- Op de externe link : International Slide Rule Museum is een afbeelding opgenomen van Mr. Spock met een rekenschijf.
![]()
![]() Zie ook de categorie met mediabestanden in verband met Slide rule op Wikimedia Commons.
Zie ook de categorie met mediabestanden in verband met Slide rule op Wikimedia Commons.

