Wikisage, de vrije encyclopedie van de tweede generatie, is digitaal erfgoed

Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.

  • Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
  • Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
rel=nofollow

Onderscheidend vermogen: verschil tussen versies

Uit Wikisage
Naar navigatie springen Naar zoeken springen
(Het onderscheidend vermogen van een statistische toets is de kans om een nulhypothese terecht te verwerpen. ([http://nl.wikipedia.org/w/index.php?title=Onderscheidend_vermogen&oldid=16726727]))
 
kGeen bewerkingssamenvatting
 
(Een tussenliggende versie door dezelfde gebruiker niet weergegeven)
Regel 6: Regel 6:
Twee [[normale verdeling|normaal verdeelde]] populaties A en B met een verschillende behandeling worden vergeleken op basis van steekproeven ''X'' respectievelijk ''Y'', elk van omvang ''n''. De standaardafwijkingen van beide populaties zijn gelijk, zeg σ, en de hypothesen voor de verwachtingswaarden luiden:
Twee [[normale verdeling|normaal verdeelde]] populaties A en B met een verschillende behandeling worden vergeleken op basis van steekproeven ''X'' respectievelijk ''Y'', elk van omvang ''n''. De standaardafwijkingen van beide populaties zijn gelijk, zeg σ, en de hypothesen voor de verwachtingswaarden luiden:


:<math>H_0:\ \mu_A = \mu_B\, </math>  
<br>
[[Afbeelding:onderscheidend_vermogen_1.jpg|150px|left]] <br><br><br>
tegen  
tegen  


:<math>H_1:\ \mu_A > \mu_B\, </math>
<br>
[[Afbeelding:onderscheidend_vermogen_2.jpg|150px|left]] <br><br><br>


Als toetsingsgrootheid ''T'' komt in aanmerking:
Als toetsingsgrootheid ''T'' komt in aanmerking:


:<math>\bar{X}-\bar{Y}</math>,
<br>
[[Afbeelding:onderscheidend_vermogen_3.jpg|60px|left]] <br><br>


maar om de berekeningen eenvoudiger te maken kiezen we:
maar om de berekeningen eenvoudiger te maken kiezen we:


:<math>T = \frac{\bar{X}-\bar{Y}}{\sigma}\sqrt{\frac n2}</math>,
<br>
[[Afbeelding:onderscheidend_vermogen_4.jpg|150px|left]] <br><br><br><br>


Gezien de alternatieve hypothese wordt ''H''<sub>0</sub> verworpen voor grote waarden van ''T''. De kritieke waarde is ''z''<sub>α</sub>, bepaald door:
Gezien de alternatieve hypothese wordt ''H''<sub>0</sub> verworpen voor grote waarden van ''T''. De kritieke waarde is ''z''<sub>α</sub>, bepaald door:


:<math>P(T\geq z_\alpha|H_0) = \alpha</math>,
<br>
[[Afbeelding:onderscheidend_vermogen_5.jpg|150px|left]] <br><br>


waarin α de verlangde [[onbetrouwbaarheid (statistiek)|onbetrouwbaarheid]] is. Het onderscheidend vermogen van deze toets is nu:
waarin α de verlangde [[onbetrouwbaarheid (statistiek)|onbetrouwbaarheid]] is. Het onderscheidend vermogen van deze toets is nu:


:<math>\gamma(\Delta) = P(T\geq z_\alpha|\mu_A-\mu_B=\Delta)=P\left(T-\frac{\Delta}{\sigma}\sqrt{\frac n2} \geq z_\alpha-\frac{\Delta}{\sigma}\sqrt{\frac n2}|\mu_A-\mu_B=\Delta\right)=P\left(Z>z_\alpha-\frac{\Delta}{\sigma}\sqrt{\frac n2}\right)</math>,
<br>
[[Afbeelding:Verbeterde_versie.jpg.jpg|800px|left]] <br><br>


gedefinieerd voor Δ > 0. Daarin is ''Z'' standaard normaal verdeeld.
gedefinieerd voor Δ > 0. Daarin is ''Z'' standaard normaal verdeeld.

Huidige versie van 15 dec 2010 om 18:02

Zie ook : onderscheidingsvermogen, voor een andere betekenis van "onderscheidingsvermogen".

Het onderscheidend vermogen oftewel onderscheidingsvermogen (Engels : discernment / discrimination) van een statistische toets is de kans om een nulhypothese terecht te verwerpen. Met andere woorden: de kans dat de test geen fout-negatief geeft. Het onderscheidend vermogen is de complementaire kans van de kans op een fout van de tweede soort (type II-fout). Omdat de alternatieve hypothese vaak samengesteld is, zal het onderscheidend vermogen een functie zijn, wel aangegeven door γ, van de mogelijke waarden van de betrokken parameter onder de nulhypthese. Men gaat soms zelfs zover dat men deze functie uitbreidt tot alle waarden van de betrokken parameter, ook die onder de nulhypothese.

Voorbeeld

Twee normaal verdeelde populaties A en B met een verschillende behandeling worden vergeleken op basis van steekproeven X respectievelijk Y, elk van omvang n. De standaardafwijkingen van beide populaties zijn gelijk, zeg σ, en de hypothesen voor de verwachtingswaarden luiden:





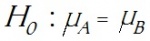
tegen





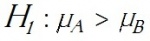
Als toetsingsgrootheid T komt in aanmerking:




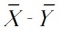
maar om de berekeningen eenvoudiger te maken kiezen we:






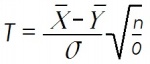
Gezien de alternatieve hypothese wordt H0 verworpen voor grote waarden van T. De kritieke waarde is zα, bepaald door:




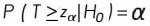
waarin α de verlangde onbetrouwbaarheid is. Het onderscheidend vermogen van deze toets is nu:




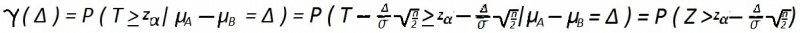
gedefinieerd voor Δ > 0. Daarin is Z standaard normaal verdeeld.

Zie ook

Overgenomen van "https://nl.wikisage.org/w/index.php?title=Onderscheidend_vermogen&oldid=59362"