Over het minimum oppervlak van een cilinder

Dit is een gebruikersessay geschreven door Franciscus 2 november 2016 15:00 (UTC)

In het essay over het minimum oppervlak van een kegel, wordt aangetoond, dat bij het groter of kleiner worden van de straal R – bij een gegeven inhoud V - niet alleen het oppervlak A van de kegel groter of kleiner wordt, maar dat er ook een kleinste oppervlak aanwezig is.
Bij een cilinder blijkt bij een gegeven inhoud V ook een kleinste oppervlak A te bestaan, of met andere woorden:

• Het oppervlak A van een cilinder bereikt - bij een gelijkblijvende inhoud V - een limiet bij wijziging van de straal R en de hoogte h.

Deze stelling zal hierna verder worden onderzocht.

Cilinder

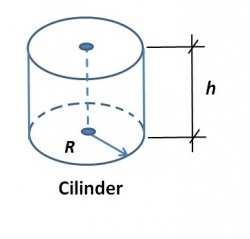
Een Cilinder bestaat uit een gebogen oppervlak of cilindermantel, een grondvlak en een bovenvlak. Het bovenvlak is gelijk aan het grondvlak. Bij de berekening van het oppervlak A en de inhoud V, komt het getal π aan de orde.
De algemeen gebruikte formules voor het oppervlak A en de inhoud V zijn als volgt:

• Voor de uiteenzetting over het minimum oppervlak, worden deze formules iets anders genoteerd, door namelijk uit te gaan van de diameter d = 2R in plaats van de straal R:

Standaardconservenblik

We zullen nu eens gaan onderzoeken bij welke afmetingen van hoogte h en diameter d het minimumoppervlak A_min aanwezig is.
Wiskundig kan dit allemaal op eenvoudige wijze worden uitgevoerd met limieten, maar dan mis je tamelijk snel het inzicht van wat er gaande is. Om die reden zullen we hier dan ook met een rekenvoorbeeld uit de praktijk werken, namelijk met een standaardconservenblik, zoals we die in de vakken van de supermarkt zien staan.
Een conservenblik heeft uitwendig de vorm van een cilinder, waar als het ware een kleinere cilinder is uitgehaald, waardoor er een holle cilinder overblijft.
De meest voorkomende conservenblikken, gevuld met bruine bonen, sperciebonen, erwtensoep, of een ander product, zijn blikken met een diameter van 10 cm en met een hoogte van 11 cm, zodat de inhoud hiervan - rekening houdend met de materiaaldikte van 0,25 mm circa 0,85 liter is. Op de wikkel van veel blikken staat, dat er 0,8 of 0,83 liter inzit, zodat de blikken niet tot de rand gevuld zijn. Dat is ook wel nodig, om het uitzetten van het product op te kunnen vangen. Verder moet er natuurlijk voor worden gezorgd, dat de door de spreiding bij het vulproces niet te weinig in zo’n blik terecht komt. Dat houdt dus in, dat er meestal iets meer van het product in het blik wordt gedaan, om zeker te zijn, dat de afnemer tevreden is.

Minimum en maximum

Het ligt natuurlijk voor de hand, dat de fabrikant - die grote hoeveelheden standaardblikken moet gaan vullen - graag wil, dat de stuksprijs hiervan zo laag mogelijk is. Het standaardblik moet dus liefst een zo klein mogelijk oppervlak hebben, want dan wordt er zo min mogelijk materiaal gebruikt. Ook bij het transport van de gevulde blikken moet natuurlijk zo weinig mogelijk ruimte worden ingenomen, zoals bepaald door de afmetingen van de tray of het pallet waarmee de blikken worden getransporteerd.
Wat betreft het oppervlak van het conservenblik is hier dus sprake van een minimum. Wat betreft de inhoud van het blik is hier sprake van een maximum, namelijk 0,85 liter. Deze twee uitersten zullen in één product verenigd moeten worden.
Rekening houdend met de constante inhoud V = 0,85 liter = 850 cm³, kan bij elke diameter d en de daaruit af te leiden hoogte h het oppervlak A van de holle cilinder worden berekend.

Minimum oppervlak

Als we om te beginnen eens twee uitersten nemen, bijvoorbeeld een cilinder met een diameter d₁ = 20 cm en een cilinder met een diameter d₂ = 5 cm, dan volgt uit de eerder getoonde formules, dat bij het eerste blik de hoogte h₁ = 2,7 cm en bij het andere blik h₂ ≈ 43 cm. Dat zijn nogal uitzonderlijke blikken; een laag, nogal plat blik alleen geschikt voor het opbergen van crêpes, en een hoog, uitermate slank blik, alleen geschikt voor het inblikken van asperges. De oppervlakken van deze twee blikken zijn A₁ = 719 cm² en A₂ = 798 cm².
Ons gevoel zegt, dat we wel ergens halverwege d₁ = 20 cm en d₂ = 5 cm, moeten uitkomen.
Uitgaande van de inhoud V van 850 cm³, kan bij aanname van een aantal diameters in de buurt van de 10 cm steeds het oppervlak A worden berekend. We zien dan vanzelf wel waar we uitkomen. In bijgaande tabel zijn de uitkomsten netjes gerangschikt.

Diameter d ( cm )	Hoogte h ( cm )	Oppervlak A ( cm 2 )
5	43,3	719
6	30	623
7	22,5	563
8	17,2	525
9	13,6	505
10	11	497
10,27	10,27	496
11	9,1	499
12	7,6	509
13	6,5	527
14	5,6	551
15	4,9	580
16	4,3	614
17	3,75	654
18	3,34	698
19	2,99	746
20	2,7	798

Nadere beschouwing

Het kleinste oppervlak A van het conservenblik = 496 cm² - het minimum oppervlak dus – blijkt aanwezig te zijn, als de diameter d gelijk is aan de hoogte h. Dit is het geval als h = d = 10,27 cm, zoals ook bijgaande grafiek laat zien.
In de praktijk blijkt het conservenblik dus iets af te wijken van de ideale afmetingen. De diameter d van een standaardconservenblik is 10 cm en de hoogte h is 11 cm, maar dit heeft - zoals uit de tabel en uit de grafiek blijkt - nauwelijks invloed op het blikoppervlak A, zodat toch volledig wordt voldaan aan de gestelde eisen met betrekking tot het materiaalverbruik en de kosten.

Nawoord

De simpele waarneming van een in elke supermarkt te vinden standaardconservenblik heeft geleid tot een nadere beschouwing van de cilinder, waarbij gebleken is, dat bij een constante inhoud V en bij wijziging van de diameter d, het oppervlak A groter of kleiner wordt. Het blijkt verder dat dit stijgen en dalen van het oppervlak A uitmondt in een minimum oppervlak, en wel als de hoogte h = diameter d, of anders geformuleerd:

• Het oppervlak A van een cilinder bereikt bij een gelijkblijvende inhoud V

een limiet bij wijziging van de straal d en de hoogte h.

Deze limiet wordt bereikt als de straal d en de hoogte h gelijk aan elkaar zijn.