De meter

Dit artikel valt onder beheer van Dorp:Maatdam.

De meter

Wij vinden het doodgewoon om, als er iets gemeten moet worden, dat te doen met een duimstok of een liniaal met de lengtemaat meter als uitgangspunt.
De meter geldt al geruime tijd als standaard voor onze lengtematen.
In de eeuwen vóór ons was dat allemaal niet zo vanzelfsprekend. Pas aan het eind van de 19e eeuw werd in ons land de meter als eenheid van lengte ingevoerd, met de bedoeling een eind te maken aan de grote verscheidenheid aan maat- en gewichteenheden. Vóór die tijd waren in ons kleine landje minstens 55 verschillende maten in gebruik, uitgedrukt in allerlei eenheden. Ook bij de inhoudsmaten en gewichten kon je spreken van een bonte verzameling.
Dit bracht natuurlijk allemaal de nodige verwarring en onenigheid met zich mee, iedere keer weer als er iets verhandeld moest worden, maar vooral als er stads- of provincie-overschrijdende handel werd bedreven, om maar niet te spreken over de problemen die er waren als er voor de handel landsgrenzen moesten worden overschreden.

Orde in de chaos

Om orde in de chaos te scheppen, waren op den duur omrekentabellen en andere hulpmiddelen nodig, aangezien anders geen normale transacties meer konden worden afgesloten. Ook de handel met het buitenland had voortdurend met deze verschillen te kampen, vooral als men meende over dezelfde maten te spreken. Men leidde bijvoorbeeld de lengtematen onder meer af van de gemiddelde duim van drie volwassen mannen. Nog fraaier was de lengtemaat waarbij de voet werd gebruikt. Hiervoor werd

• de gemiddelde voet aangehouden van een twaalftal mannen die ’s zondags uit de kerk kwamen!

Voor de el ( = 67 cm ) werd eerst de lengte van de elleboog tot de top van de middelvinger genomen. Later rekende men van de oksel tot de middenvinger.
Het zal duidelijk zijn, dat dit allemaal niet zo vreselijk nauwkeurig was, en dat er ook nogal wat verschillen ontstonden, die veel problemen opleverden en onenigheid gaf. Verschillen in lengte van 30% waren hierbij geen uitzondering. Dit alles vroeg erom om meer gestandaardiseerd te gaan werken.
In sommige steden was men al zover, dat er een soort standaard werd aangehouden. Zo’n standaard – meestal van ijzer gemaakt – was dan aan het stadhuis bevestigd, zodat iedereen daar gebruik van kon maken en een vast ijkpunt had.

Eerste pogingen

Christiaan Huygens wilde al in 1664 een universele lengtestandaard invoeren, die afgeleid was van

• de lengte van een slinger die in één seconde een volledige slingering uitvoert.

Deze eenheid werd ook in andere landen als een mogelijke optie gezien.
In 1670 stelde de Franse abt Mouton voor om de universele lengtemaat

• af te leiden van de omtrek van de aarde.

Op die manier was men niet meer afhankelijk van een lengtemaat die gebaseerd was op menselijke ledematen als de voet, de duim of de el. Men kon op die manier zonder sentimenten gestandaardiseerde maateenheden gaan voeren die zowel nationaal als internationaal zouden kunnen worden gehanteerd. Dit idee werd lange tijd gekoesterd, maar het zou nog tot de beginjaren van de Franse revolutie duren voordat men overging tot de praktische uitvoering daarvan.

Meting van de aardomtrek

Het idee om de omtrek van de aarde te meten, was al eerder ontwikkeld door de Griekse meetkundige Erastothenes, die van 275 tot 194 voor Christus leefde. Erastothenes, die wist dat de aarde rond was, bepaalde met twee meetstokken van gelijke lengte met behulp van een assistent de hoek die de zon op 21 juni om 12 uur ’s middags op twee plaatsen maakt.
Zijn assistent was hiertoe in Cyrene nabij Aswan in Egypte gereisd en nam plaats op de plek waar om 12 uur de zon loodrecht boven de aarde staat, waardoor de loodrecht geplaatste meetstok dus geen schaduw op de grond wierp. In Alexandrië was er om 12 uur ’s middags wél een schaduw, en mat Eratosthenes de lengte van de kleinste schaduw die de zon met de meetstok maakte. Met behulp van eenvoudige meetkunde – die toen al bekend was – bepaalde hij de hoek die de stok met de aarde maakte. Die bleek 7 ⁰ en 12′ te bedragen, dus 7,2 graden.
De afstand van Alexandrië tot Cyrene was bekend, namelijk 5000 stadiën, wat ongeveer overeenkomt met 783,72 km. Aangezien een cirkel 360 ⁰ omvat, kon met dezelfde eenvoudige meetkunde worden vastgesteld, dat de omtrek van de aarde 5000 ∙ 360 ⁰ ∕ 7,2 ⁰ = 250.000 stadiën bleek te zijn, wat in de buurt ligt van 39.186 km. Het is namelijk zó, dat men niet geheel zeker is van de juiste lengte van de stadiën, zodat dus de berekende afstand groter of kleiner kan zijn dan 39.186 km.
Maar hoe dan ook, het blijft een een opmerkelijk resultaat!

Definitie van de meter

In 1791 werd door de Académie des Sciences het oude idee van de abt Mouton weer opgepakt en besloten een deel van de omtrek van de aarde tot eenheid van lengte verklaren, met de van het Griekse woord metrum ( = μετρητής ) afgeleide naam: meter.
In hun rapport werd deze eenheid van lengte omschreven als

• het tienmiljoenste deel van de afstand rond het aardoppervlak ( meridiaanboog ), vanaf de noordpool tot aan de evenaar, langs de meridiaan van Parijs.

Anders gezegd:

• het veertigmiljoenste deel van de gehele aardomtrek, gemeten langs de toen nog geldende nulmeridiaan van Parijs.

Ook te omschrijven als: De letter Q stelde 1 ∕ 4 van de nulmeridiaan voor, zodat de lengte van de meter kon worden geformuleerd als:

• 1 meter = 10 ⁻⁷ Q.

Besloten werd om het gedeelte van de meridiaan tussen Duinkerken en Barcelona te meten, en dan de gemeten lengte te extrapoleren tot 10 ⁻⁷ Q. De meridiaan werd daartoe in twee ongelijke delen verdeeld. Het eerste deel liep van Duinkerken tot Rodez en het tweede deel van Rodez tot Barcelona. De Franse geleerden hadden het hart van Parijs als plek uitgekozen waar een meridiaan via Duinkerken naar Barcelona en verder liep. Voor het gemak hadden zij deze meridiaan maar de Nulmeridiaan genoemd.

Nulmeridiaan

Kaart uit 1972 van Michelin met nulneridiaan over Parijs en andere steden als Doullens. Doullens ligt halverwege Duinkerken/Parijs

Een meridiaan is in de aardrijkskunde een halve cirkel op het aardoppervlak tussen de noordpool en de zuidpool.

• De keuze van de nulmeridiaan is lange tijd omstreden geweest. In het verleden zijn er dan ook nogal wat meridianen als nulmeridiaan aangenomen, waaronder die door belangrijke steden als Parijs, Rome, Kopenhagen, Jeruzalem en Sint Petersburg. Uiteindelijk is in oktober 1884 de meridiaan die door het Koninklijk Observatorium Greenwich loopt, als dé internationaal geldende Nulmeridiaan gekozen op de Internationale Meridiaanconferentie. Van de aanwezige landen stemden alleen Brazilië en Frankrijk tegen.
• Frankrijk heeft zijn eigen nulmeridiaan nooit echt willen opgeven. Na eeuwen van Frans-Britse oorlogen werd de komst van de nulmeridiaan van Greenwich beschouwd als een onverdedigbare en onomkeerbare Britse cartografische invasie van het eigen grondgebied. Maar onder grote druk van de andere landen zag Frankrijk zich toch gedwongen met de rest van de wereld de Greenwich-meridiaan als universele nulmeridiaan te aanvaarden. Frankrijk accepteerde de nulmeridiaan van Greenwich echter pas officieel in 1911.
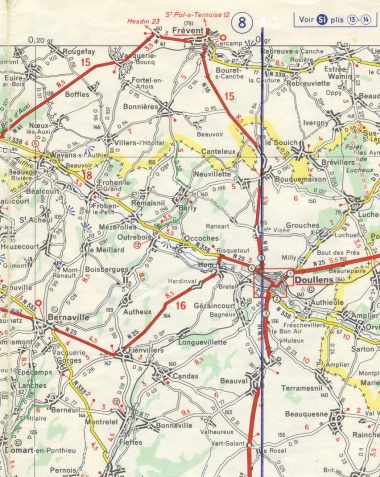
• Op de landkaarten van Michelin, is de nulmediaan die over Parijs en andere steden als Amiens en Doullens liep tot ongeveer 1980 nog steeds aanwezig. Pas later is dit herzien, waardoor Parijs nu op 2 ^o 20 ^, oosterlengte ligt ten opzichte van de nulmeridiaan van Greenwich.

Meetopdracht

Jean-Baptiste-Joseph Delambre ( 1749 – 1822 )

Pierre-François-André-Méchain ( 1744 – 1804 )

Het enige wat na het besluit van de Académie des Sciences nu nog moest gebeuren, was de gekozen afstand nauwkeurig te gaan meten.
Op 5 mei 1792 werd de meetopdracht toevertrouwd aan Jean-Baptiste-Joseph Delambre en Pierre-François-André Méchain; twee vooraanstaande Franse astronomen die allebei al een flinke staat van verdienste hadden opgebouwd.
Mechain had als taak het zuidelijke deel te meten, van Rodez tot Barcelona en Delambre moest het noordelijke deel van Duinkerken tot Rodez voor zijn rekening nemen. Hij zou vervolgens ook in zuidelijke richting afdalen om met zijn collega Mechain verder alles af te ronden.
Met flinke onderbrekingen trokken beide wetenschappers zeven jaar lang, vergezeld door hun assistenten, elk in een eigen richting langs de Nulmeridiaan van Parijs. Zij hielden contact met elkaar door middel van briefwisseling, wat in die dagen niet altijd even florissant verliep.
Deze hele operatie gebeurde in een land dat nogal onrustig was maar waar ook de bevolking op het platteland en in de kleine steden uitermate argwanend tot vijandig tegenover de metingen stond. Door dit alles werd hun het meten zeer moeilijk gemaakt, werden ze lastig gevallen of zelfs gevangen gezet en konden ze soms tijden lang niet verder met hun opdracht. De uitvoering van het project ondervond hierdoor nogal wat moeilijkheden, onderbrekingen en problemen, niet het minst omdat ondertussen niet alleen de Franse revolutie, maar ook een oorlog met Spanje was uitgebroken.
Intussen ging natuurlijk ook de nodige tijd zitten in het meten zelf.

Begin van de metingen

Na wat voorbereidingen werd in juni 1792 begonnen met de afstand tussen Duinkerken en Barcelona te meten. Vooral in die tijd natuurlijk een gigantisch karwei. De bedoeling hiervan was de verkregen meetgegevens om te zetten in bruikbare tabellen, waarna een commissie alle gegevens zou narekenen om tenslotte hieruit het veertigmiljoenste deel van de aardomtrek vast te stellen, gemeten langs de nulmeridiaan van Parijs. Het enige wat er tenslotte nog gedaan moest worden, was het samenvatten van deze gegevens en de resultaten hiervan in één enkel getal uit te drukken: de meter.

Meetmethode

Het precieze meten werd uitgevoerd met behulp van voor die tijd zeer nauwkeurige meetinstrumenten en met de nu nog steeds in gebruik zijnde methode van driehoeksmetingen.
Een driehoeksmeting of triangulatie is een meting waarbij men gebruik maakt van de eigenschap van een driehoek, namelijk dat een driehoek volledig is bepaald als we één zijde (de basis) en de aanliggende hoeken kennen. Bij de driehoeksmeting wordt gebruik gemaakt van formules uit de goniometrie, met name de sinusregel.
Om nog nauwkeuriger te werken, werden bij deze landmetingen ketens van driehoeken gehanteerd, waardoor een volkomen sluitend resultaat kon worden bereikt. Om de metingen praktisch te kunnen uitvoeren, werd vanuit goed herkenbare plaatsen in het landschap gemeten, zoals kerktorens of forten. Als die ontbraken, moesten ze zelf bakens bouwen om de metingen te kunnen voltooien.
Om het geheel te kunnen controleren, werd ook gebruik gemaakt van boldriehoeksmeting of sferische trigonometrie, die toen al behoorlijk goed ontwikkeld was. Deze wetenschap wordt toegepast bij afstandsberekeningen tussen twee punten op het aardoppervlak als hun geografische coördinaten gegeven zijn, uitgedrukt in lengte- en breedtegraden.
Lengte- en breedtegraden zijn denkbeeldige lijnen die over de wereldbol zijn getrokken. Van Noord naar Zuid noemt men die lijnen een lengtegraad. Een lijn van Oost naar West heet een breedtegraad. De oorsprong van de breedtegraden ligt bij de vroegere scheepsvaarders.
Bij de berekeningen van afstanden tussen twee punten op het aardoppervlak, veronderstelt men de aarde als zuiver bolvormig.

Van een meter die geen meter is

Uiteindelijk werden alle meetgegevens, na een verzamelperiode die zeven jaar in beslag nam, voorgelegd aan een team van geleerden die in een conferentie te Parijs bijeen waren gekomen om gezamenlijk de juiste lengte van de meter vast te stellen. De meetresultaten werden overigens wat betreft de lengtematen nog uitgedrukt in lignes, overeenkomend met ongeveer 2,255 mm.
De commissieleden onderwierpen de meetresultaten aan een nauwgezet onderzoek, waarbij alle gegevens en alle hoeken van elk meetpunt werden geverifieerd. Het enige wat nu nog moest gebeuren, was de meetgegevens samen te vatten tot het ene getal waar alles om begonnen was:

• de lengte van de meter.

Toen de geleerden hun geodetische berekeningen voltooiden, werd het echter steeds duidelijker, dat er iets niet helemaal in orde was. De resultaten van de landmetingen waren schokkend en in eerste instantie onverklaarbaar. Uit de gegevens van Delambre en Méchain kwam namelijk naar voren, dat de aarde onronder was dan men tot dan toe had aangenomen. Praktisch gezien kwam het er op neer, dat het door de grillige vorm van de kleine sector tussen Duinkerken en Barcelona onjuist was om hieruit zonder correcties de gehele meridiaanlengte af te leiden, waardoor ook het uitgangspunt onhoudbaar werd, namelijk dat de gemeten meridiaan model zou kunnen staan voor de lengte van alle meredianen.
De vraag was natuurlijk welke consequenties dit alles had voor de bepaling van de meter. De commissie stond nu voor een dilemma. Na lange discussies werden de nieuwe inzichten in de afwijking van de bolvorm gelaten voor wat ze waren en werd uitgegaan van bestaande gegevens. Door deze beslissing werd de uiteindelijke lengte van de meter iets korter dan bij aanhouden van gecorrigeerde meetgegevens het geval zou zijn geweest. De definitieve meter kreeg een lengte van 443,296 lignes = 10 ⁻⁷ Q = 0,999771 m. Deze maat wijkt enigszins af van de uit de omtrek van de aarde berekende lengte zoals deze nu bij ons bekend is, en die met moderne middelen is vastgesteld.
Later wilde Méchain – vermoedelijk om zichzelf gerust te stellen – nog aanvullende metingen uitvoeren aan de Frans-Spaanse grens.
Dit is hem noodlottig geworden. Ten eerste had hij veel tegenslag tijdens deze missie, en er heerste malaria in het moerasachtige gebied waar hij met zijn team de metingen verrichte. Ook Méchain werd getroffen door de ziekte en overleed daaraan op 18 september 1804, kort na zijn 60 ^ste verjaardag.

Standaardmeter

Het enige wat na de definitie van de meter nog moest gebeuren, was de vastgestelde lengte van de meter in een standaard uit te drukken.
Men koos voor het metaal platina. Platina was in die dagen nog niet zolang bekend, was zeer duur en viel uitermate moeilijk te bewerken. Door de gunstige eigenschappen van platina, als onverwoestbaarheid en een geringe uitzettingscoëfficiënt was het echter uitermate geschikt als standaard van de meter.
De vermaarde instrumentmaker Etienne Lenoir kreeg in 1799 de opdracht de definitieve meter in platina te gieten. Hiervoor kreeg hij vier staven zuiver platina, met het doel van de vier, met 10% iridium gelegeerde staven, één ervan na het gieten tot standaardmeter te verklaren. De nauwkeurigste staaf – die de definitieve lengte tot 0,0001 procent benaderde – werd uiteindelijk als dè meetstandaard ( Mètre des Archives ) gekozen en werd bewaard in het Archive National.
Toen enkele jaren later bleek wat de werkelijke afwijking van de bolvorm was, kwam men erachter, dat de standaardmeter 0,229 millimeter te kort was. Gelukkig was men zo verstandig om de opgeborgen standaardmeter ongewijzigd te laten en deze te blijven beschouwen als dé eenheid van lengte.
In 1875 werd na nauwkeurig opmeten van de bestaande standaardmeter een nieuwe standaard van platina gegoten, met een x-vormige doorsnede en opgeborgen in het Bureau International des Poids et Mesures. Kopieën hiervan zijn in vele landen aanwezig.
De eenheid van massa, het kilogram, werd vervolgens afgeleid van de meter. Eerst nam men water als standaard, door een kubieke meter water als basis te nemen, wat dus 1000 kg is. Later ging men over tot de in de praktijk onpraktische gram en weer later werd het kilogram gekozen. Deze standaard werd uiteindelijk ook in platina uitgevoerd en geldt nu als eenheid van massa. Deze standaard is eveneens veilig opgeborgen in het Bureau International des Poids et Mesures in Parijs.

Rapportage

Na de dood van Méchain in 1804 stond Delambre alleen voor de taak de metingen en alle bijbehorende gegevens in een rapport neer te leggen. Dit rapport werd voltooid in 1806 en draagt als titel:

wat dus betekent: Uitgangspunt van het metrisch decimaal systeem of de meting van de booglengte van de meridiaan tussen Duinkerken en Barcelona, uitgevoerd in 1792 en de jaren daarna.

Op de titelpagina van het rapport, dat nu veilig opgeborgen ligt in de kluis van Karpeles Manuscript Museum in Santa Barbara in Californië, heeft Delambre de historische woorden geschreven die Napoleon Bonaparte uitsprak bij het aanvaarden van de meter als standaard:

• Les conquêtes passent et des operations restent,

wat dus betekent:

• Veroveringen zullen komen en gaan, maar dit werk zal blijvend zijn.

In het eerste deel van dit ongeveer 1000 bladzijden bevattende rapport, zijn – naast de geschiedenis van het project – ook de triangulatiegegevens opgenomen. Het tweede deel van 1807 bevat de gegevens van de nauwkeurige breedtegraadmetingen van Duinkerken en Barcelona en het derde deel, dat in 1810 verscheen, behandelt de foutcorrecties en excentriciteit van de aarde.

Invoeren van de meter

Het invoeren van de meter als lengte-eenheid ging, zoals te begrijpen valt, allemaal niet zo erg gemakkelijk. Er werden natuurlijk veel traditionele en aan het vak gebonden maateenheden gehanteerd, die je niet zomaar van de ene dag op de andere dag kon afschaffen.
Als we denken aan de invoering van de euro, dan wordt natuurlijk al snel duidelijk, dat er problemen moesten ontstaan. Ook nu betrappen we ons er af en toe nog steeds op, dat we – vooral als het grote bedragen zijn – toch nog even naar guldens omrekenen. Ongeveer zo moet het zijn gegaan het bij de invoering van de meter en het kilogram.
In Frankrijk ging men over op de meter in 1840, waarbij men de landen die onder het eerste keizerrijk vielen ook gelijk maar dwingend oplegde de meter als standaard te aanvaarden. Nederland en België hadden de meter echter al eerder omarmd. Duitsland had veel moeite met het aanvaarden van het metrieke stelsel, maar gaf zich uiteindelijk toch gewonnen. Ook in Rusland werd pas onder het bewind van de Sovjet-Unie de meter als verplichte eenheid aanvaard.
En Engeland dan? Dat is een geval apart.
Pas in 1965 kondigde de Britse regering een overgangsperiode van 10 jaar aan om te wennen een het metrieke stelsel, waarin gelijk de landen van het Gemenebest werden meegenomen.

Decimale stelsel

Zoals in het rapport van Delambre was aangegeven, hoorde bij de invoering van de meter ook gelijk een invoering van een Decimaal Stelsel. Vóór die tijd kregen grotere of kleinere afmetingen dan bijvoorbeeld de el of de voet andere benamingen. Bij de komst van de meter werden vóór de afkorting m ( = meter ) decimale aanduidingen geplaatst als er grotere of kleinere afmetingen dan de meter moesten worden aangeduid.
In de tabel zijn de meest gangbare aanduidingen opgenomen.

Factor	Naam	Symbool
10 − 12	picometer	pm
10 − 9	nanometer	nm
10 − 6	micrometer	µm
10 − 3	millimeter	mm
10 − 2	centimeter	cm
10 − 1	decimeter	dm
10 0	meter	m
10 1	decameter	dam
10 2	hectometer	hm
10 3	kilometer	km
10 4	Myriameter; miriameter	mam

Bronnen

• Ken Adler, The measure of All Things, Time Warner Books UK.
• (Nederlandse vertaling van bovenstaand boek:)
  De maat van alle dingen. De zevenjarige zoektocht naar de universele meter, Ambo|Anthos uitgevers, Amsterdam, ISBN 90 414 0569 0