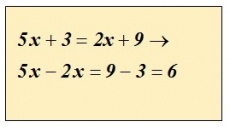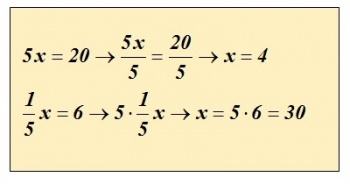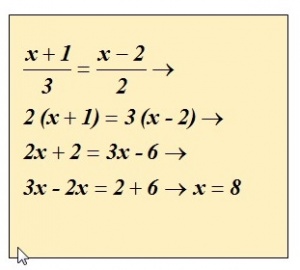Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Algebra ( Vergelijkingen )
In Algebra ( 4 ) werden de onderwerpen Machtsverheffen en Worteltrekken behandeld. In Algebra ( 5 ) komen Vergelijkingen aan de orde.
Bij vergelijkingen wordt meestal de letter x gebruikt, en soms ook de y en de z.
Eenvoudige vergelijkingen
Er is sprake van een vergelijking, als twee vormen worden gescheiden door het = teken, zoals in het voorbeeld is gegeven.
De oplossing van de onbekende x gebeurt in het algemeen door het toepassen van de geldende regels voor het rekenen.
Lineaire vergelijkingen met één onbekende
In het volgende voorbeeld wordt aangegeven hoe de oplossing van zogenaamde vergelijkingen van de eerste graad met één onbekende tot stand komen. Bij de oplossing hiervan geldt:
Nog een voorbeeld:
Vergelijkingen met breuken worden aldus opgelost:
Vergelijkingen als evenredigheden
Een vergelijking in de vorm van een evenredigheid kan worden opgelost door kruislings vermenigvuldigen, dus :
Vergelijkingen van de tweede graad met twee onbekenden
Bij twee lineaire vergelijkingen met twee onbekenden wordt of x óf y als onbekende opgelost, waardoor dan de andere onbekende term bekend wordt. Dit gebeurt, door één vergelijking dusdanig te bewerken, dat of x óf y tegenover elkaar wegvallen, aldus:
Vergelijking van de tweede graad met één onbekende
De kwadratische vergelijking van de tweede graad, die ook wel vierkantsvergelijking wordt genoemd, kan soms vrij gecompliceerd worden.
Een vierkantsvergelijking is een vergelijking, die deze vorm heeft:
In deze vergelijking zijn a , b en c constante getallen, waarbij a nooit 0 zal zijn. Verder zal het duidelijk zijn, dat er twee oplossingen ( x1 en x2 ) zullen zijn, aangezien de wortelvorm zowel een positieve als een negatieve uitkomst heeft. Dit is in ( Algebra 4 ) al behandeld.
( De herkomst en de bijzondere voorwaarden die aan deze vergelijking zijn verbonden, worden hier achterwege gelaten.)
Met een rekenvoorbeeld zal deze vergelijking worden toegelicht.
Van de rechthoek zijn de volgende gegevens bekend:
- De omtrek O = 26 cm = 2 (x + y)
- Het oppervlak A = 36 cm 2 = x • y
Gevraagd wordt de lengte en de breedte van de rechthoek te berekenen.
( In de uitwerking van de formule wordt voor de eenvoud bijna alleen met getalwaarden gewerkt en niet met lengtematen.)
:

De twee uitkomsten x1 = 9 en x2 = 4 komen op hetzelfde neer, namelijk:
- breedte x1 = 9 geeft een lengte y1 = 13 – 9 = 4 cm
- breedte x2 = 4 geeft een lengte y2 = 13 – 4 = 9 cm
De rechthoek heeft dus – zoals was gegeven – een omtrek: O = 2 (4 + 9) = 26 cm, en een oppervlak A = 4 • 9 = 36 cm 2.