Essay:Over kwadraten

Dit is een gebruikersessay geschreven door Franciscus 1 augustus 2009 16:00 (UTC)

Het woord kwadraat stamt af van het Latijnse woord quadratus, dat weer afkomstig is van quadrus. Quadrus betekent zoveel als vierkantig maken.
In onze beleving heeft het woord kwadraat de betekenis gekregen van een getal, dat met zichzelf wordt vermenigvuldigd. Dit zou geschreven kunnen worden als:

• n . n

waarbij n het getal voorstelt, dat wordt gekwadrateerd. Men heeft er echter voor gekozen het kwadraat van n weer te geven, als:

• n ²

Kwadraten

De kwadraten 1 ², 2 ², 3 ² en zo voorts, kunnen op een eenvoudige wijze grafisch worden weergegeven, zoals op de afbeeldingen is te zien. Over 1 ² valt niet veel te vertellen, aangezien 1 . 1 = 1. Bij 2 ²,
3 ² en zo voorts, wordt dit anders. De twee groene stippen stellen het getal 2 voor. Aangezien 2 ² = 2 . 2 = 4, komt er dus een rij met groene stippen bij, en ontstaat er een vierkant.
We komen hiermee weer uit bij quadrus, dus het vierkantig maken van een getal.
Bij het getal 3 gaat het precies zo. Het getal 3 wordt hier weergegeven door drie groene stippen. Aangezien 3 ² = 3 . 3 = 9, komen er dus twee rijen met groene stippen bij. Hetzelfde verhaal gaat op voor elk ander getal, ook voor halve getallen of breuken.
In principe kan elk getal grafisch worden weergegeven, al is dit bij halve getallen of breuken wat gecompliceerder dan bij hele getallen.
In het verdere betoog zal vanwege de eenvoud, daarom steeds met hele getallen worden gewerkt.

Het verband tussen de kwadraten

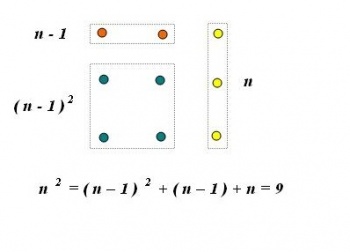
Het blijkt, dat bij de reeks kwadraten, gerekend vanaf 1 ², 2 ², 3 ² en zo voorts, tussen twee opvolgende kwadraten een samenhang bestaat. Tussen twee opvolgende kwadraten blijkt namelijk de volgende betrekking aanwezig te zijn:

• n ² = ( n – 1 ) ² + ( n – 1 ) + n

Voor bijvoorbeeld 3 ² ( dus n = 3 ) in betrekking tot n - 1 = 2, geldt dus:

• 3 ² = ( 3 – 1 ) ² + ( 3 – 1 ) + 3 = 4 + 2 + 3 = 9

In bijgaande afbeelding is dit verband op een grafische manier weergegeven.
De term ( n – 1 ) ² - weergegeven in groen - is gelijk aan ( 3 – 1 ) ² = 4.
De term ( n – 1 ) - weergegeven in rood – is gelijk aan ( 3 – 1 ) = 2 en tenslotte is de term n = 3 weergegeven in geel. Het geheel levert de som = 9 op.
Ook voor bijvoorbeeld 4 ² in betrekking tot n - 1 = 3, gaat de vergelijking op, zoals blijkt uit het volgende. Voor 4 ² ( dus n = 4 ) geldt dus:

• 4 ² = ( 4 – 1 ) ² + ( 4– 1 ) + 4 = 9 + 3 + 4 = 16

De term ( n – 1 ) ² is gelijk aan ( 4 – 1 ) ² = 9. De term ( n – 1 ) is gelijk aan ( 4 – 1 ) = 3 en tenslotte de term n = 4.
Het geheel levert de som = 16 op.
Ook als de reeks kwadraten tegengesteld loopt, kan na verandering van - in + in een vergelijking het verband tussen twee opvolgende kwadraten worden weergegeven, namelijk:

• n ² = ( n + 1 ) ² - ( n + 1 ) - n

Toegepast op de getallen 3 en 4 volgt hieruit:

• 3 ² = ( 3 + 1 ) ² - ( 3 + 1 ) - 3 = 16 – 4 – 3 = 9.

Overal verder in de reeks kwadraten blijkt de relatie met het voorgaande getal aanwezig te zijn. Neem als willekeurig voorbeeld : 21 ².

• 21 ² = ( 21 – 1 ) ² + ( 21– 1 ) + 21 = 400 + 20 + 21 = 441

en neergaand:

• 20 ² = ( 1 + 20 ) ² – ( 1 + 20 ) – 20 = 441 – 21 – 20 = 400

Tussenliggende kwadraten

Er blijken nog meer verbanden te bestaan. Als bijvoorbeeld de reeks kwadraten met een interval van twee getallen - gerekend vanaf 1 ², 3 ² , 5 ² enz., of 2 ², 4 ², 6 ² enz. - wordt bestudeerd, dan blijkt ook hier een onderlinge betrekking te bestaan.
Deze betrekking voor de reeks in de stijgende lijn wordt als volgt uitgedrukt:

• n ² = ( n – 2 ) ² + 2 ( n – 2 ) + 2 n

Als dit wordt toegepast op bijvoorbeeld het getal 5 in betrekking tot 5 - 2 = 3, dan wordt dit:

• 5 ² = ( 5 – 2 )² + 2 ( 5 – 2 ) + 2 . 5

wat dus oplevert:

• 5 ² = 3 ² + 2 . 3 + 2 . 5 = 25

Ook in afbeelding 3 is dit verband op een grafische manier weergegeven. De term ( n – 2 ) ² - weergegeven in groen - is gelijk aan ( 5 – 2 ) ² = 9. De term 2 ( n – 1 ) - weergegeven in rood – is gelijk aan 2 ( 5 – 2 ) = 6 en tenslotte is de term 2 n = 10. Het geheel levert de som = 25 op.
Als het getal 6 wordt genomen, dan levert dat op:

• 6 ² = ( 6 – 2 ) ² + 2 ( 6– 2 ) + 2 . 6

wat dus oplevert:

• 6 ² = 4 ² + 2 . 4 + 2 . 6 = 36

Voor de teruggaande reeks kwadraten wordt na aanpassing de formule aldus:

• n ² = ( n + 2 ) ² - 2 ( n + 2 ) - 2 n

Voor het kwadraat van 4 levert dit op:

• 4 ² = ( 4 + 2 ) ² - 2 ( 4 + 2 ) - 2 . 4 = 36 - 12 – 8 = 16

Algemene regel

Bij verder bestuderen van het verband tussen de kwadraten in stijgende lijn, kan een algemene formule worden opgesteld, en wel deze :

• n ² = ( n – n’ ) ² + n’ ( n – n’ ) + n . n’

waarbij n’ het vergelijkende getal is.
Bij kwadraten in neergaande lijn geldt dan de afgeleide van deze formule, namelijk:

• n ² = ( n + n’ ) ² - n’ ( n + n’ ) - n . n’

Toegepast op de opeenvolgende kwadraten met de kwadraten van 5 en 6 wordt dit:

• 6 ² = ( 6 - 5 ) ² + 5 ( 6 – 5 ) + 5 . 6 = 36

of :

• 5 ² = ( 5 + 6 ) ² - 6 ( 5 + 6 ) - 6 . 5 = 25

Toegepast op de tussenliggende kwadraten 8 ² en 10 ², levert dit op:

• 10 ² = ( 10 – 8 ) ² + 8 ( 10 – 8 ) + 10 . 8 = 100

of :

• 8 ² = ( 8 + 10 ) ² - 10 ( 8 + 10 ) - 8 . 10 = 64

Ook voor grotere intervallen geldt de algemene regel, zoals bij 7 ² en 10 ² of bijvoorbeeld 7 ² en 20 ², namelijk:

• 10 ² = ( 10 – 7 ) ² + 7 ( 10 – 7 ) + 7 . 10 = 100

en neergaand:

• 7 ² = ( 7 + 10 ) ² – 10 ( 7 + 10 ) – 7 . 10 = 49

Bij 7 ² en 20 ² wordt dit:

• 20 ² = ( 20 – 7 ) ² + ( 20 – 7 ) + 20 . 7 = 400

en neergaand:

• 7 ² = ( 7 + 20 ) ² – 20 ( 7 + 20 ) – 7 . 20 = 49

Conclusies

Het blijkt, dat er tussen twee kwadraten een onderlinge betrekking bestaat, die in formulevorm is uit te drukken.

Het onderzoek naar zo'n direct verband werd zuiver door veronderstellingen en door nieuwsgierigheid ingegeven,

en had geen functie als oplossing voor een bestaand probleem.

Door een dergelijke beschouwing blijkt er echter een proces in werking te zijn gezet, dat na uitwerking van de basisgedachte

tot verassende uitkomsten heeft geleid. Als bijkomend voordeel van dit soort overpeinzingen geldt,

dat weer eens duidelijk wordt, dat getallen niet op zichzelf staan, maar onderling met elkaar zijn verbonden.