Magisch vierkant

Een magisch vierkant of tovervierkant is een is een ordening van getallen in een vierkant waarin getallen zodanig zijn ingevuld, dat de kolommen, de rijen en de diagonalen alle dezelfde som opleveren.

Diezelfde som – een constant getal dus – wordt ook wel de magische constante genoemd..
Magische vierkanten zijn een fascinerende manier om getallen te rangschikken, en zijn zeer in populariteit gegroeid, zeker sinds de opkomst van op wiskunde gebaseerde spelletjes als Sudoku.

Oorsprong

Magische vierkanten behoren tot de oudst bekende wiskundige objecten. Als voorbeeld dient het beroemde 3 x 3 magische vierkant, wat volgens legenden uit 2800 voor Christus stamt. Het Lo Shu vierkant - zoals het magische vierkant in China wordt genoemd - is het unieke magische vierkant, waarbij het cijfer 1 aan de onderkant en 2 aan de rechterbovenhoek werd geplaatst.
De magische constante van dit vierkant = 15. De som van alle getallen in het vierkant = 45.
Het Lo Shu vierkant wordt in astrologische kringen ook wel het Saturnesvierkant genoemd.

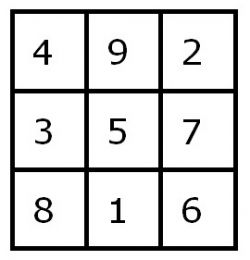
Dit vierkant heeft nog een hogere magische eigenschap, namelijk: 4² + 9² + 2 ² = 8²+ 1² + 6² =101, en
4² + 3² + 8² = 2² + 7² + 6² = 89.

Variaties

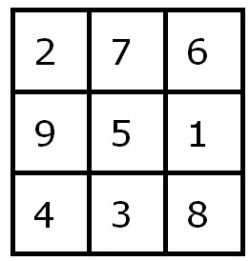
Elk magisch vierkant met drie velden kan worden verkregen uit het Lo Shu vierkant door rotatie of spiegeling. Er zijn namelijk op het Lo Shu vierkant enkele variaties mogelijk. Door kanteling van de rijen verschuiven deze, maar blijft de magische constante = 15 gelijk.

Middeleeuwen

Magische vierkanten waren in de Middeleeuwen geliefkoosde onderwerpen van de rekenkunstenaars en wiskundigen. Gesteld werd, dat een magisch vierkant een vierkant is, dat als een dambord verdeeld is in n² velden. In die n² velden zet men de getallen 1, 2,... n² zodanig, dat zij zowel horizontaal als verticaal, maar ook in de diagonalen steeds dezelfde som geven. Als klassiek voorbeeld uit die tijd werd n = 4 gekozen. Het constante getal van dit vierkant is volgens de geldende rekenkundige reeks:

• 1/2n( n² + 1 )

waarbij n = aantal velden

Ingevuld wordt dit voor n = 4:

• 2( n² + 1 ) = 34

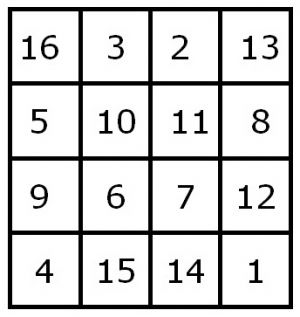
Op de afbeelding is het magische vierkant uit de berekening te zien. Duidelijk is, dat de magische constanten van de rijen en de kolommen en van de twee diagonalen allemaal = 34 zijn, en dat de som van het gehele vierkant volgens de hiervoor geldende rekenkundige reeks:

• ½ a( n² + 1 ) = 136

waarbij a = alle vierkantjes van het magisch vierkant zijn.

Extra eigenschappen

Ook bij dit vierkant zijn enkele variaties mogelijk. Door kanteling van de rijen verschuiven deze, maar blijft de magische constante gelijk = 34.

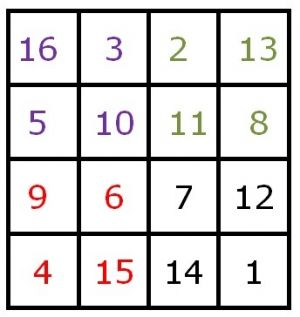
Er zijn nog meer bijzonderheden in het magisch vierkant aanwezig. Als namelijk het vierkant wordt verdeeld in vier vakken, dan is de som van die vier getallen ook steeds 34.

( 16 + 3 + 10 + 5 = 34, enz )

Verdere mogelijkheden

De gegeven vierkanten zijn het begin van een reeks magische vierkanten, die steeds ingewikkelder worden. Zo is het eerstvolgende magische vierkant een vierkant met n = 5² velden.

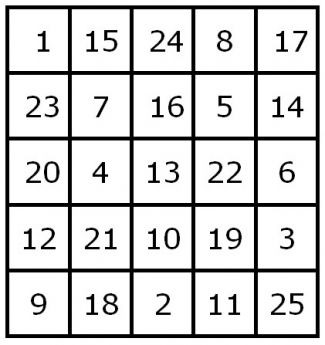
Hierbij is de magische constante:

• 1/2 n( n² + 1 ) = 2,5( 26 )= 65,

en de som van alle getallen:

• ½ a( n² + 1 ) = 12,5( 26 )= 325

Ook bij dit magische vierkant zijn allerlei variaties mogelijk. Naarmate het aantal velden n toeneemt, wordt namelijk ook het aantal variaties groter. Er zijn zelfs magische vierkanten, die driedimensionaal zijn.
Het voert te ver om hier nader op in te gaan.

Bronvermelding

Bronnen, noten en/of referenties:

• Geraadpleegde literatuur: Diverse bronnen en Quadrivium, Rekenkunde, Meetkunde, Muziek en Astronomie voor iedereen. Librero, ISBN:978-90-8998-303-9