Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Gebruiker:Franciscus/kladblok
Voorlopig neem ik deze pagina om nieuwe artikelen even op te bergen en te bewerken, vóórdat ik ze als bijdrage op Wikisage zet.
Franciscus 4 feb 2009 14:55 (UTC)
Deze afbeelding van Johan Wolfgang von Goethe is afkomstig van Wikipedia en dient als illustratie bij een artikel over Goethe. 13 feb 2009 13:26 (UTC)wil deze afbeelding gebruiken in zijn artikel: De Tovernaarsleerling. A1)

| Sjabloon:Galerijbestand | Sjabloon:Galerijbestand | Sjabloon:Galerijbestand
 Rondom de cirkelDante Alighieri heeft ooit geschreven: Lo cerchio è perfettisima figura, ofwel: De cirkel is de meest volmaakte figuur.
Benadering van de constante πOm enig inzicht in het getal π te krijgen, is een klein uitstapje naar de eenvoudige wiskunde nodig. Op de eerste afbeelding is een willekeurige cirkel weergegeven met de straal r. 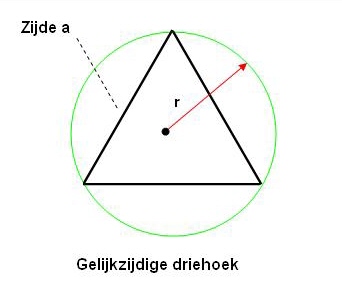 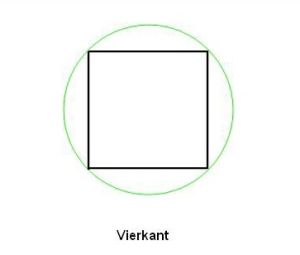 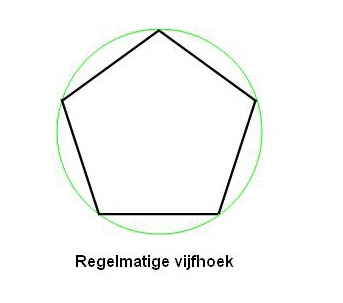 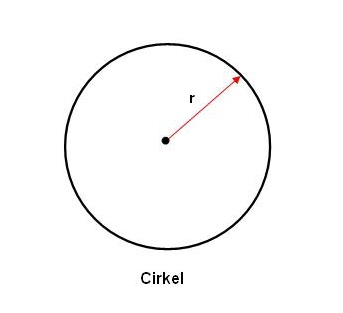 Eén zijde a van een gelijkzijdige driehoek die precies in een cirkel past, heeft een lengte van r√3, zodat dus de drie zijden van de driehoek samen 3√3r groot zijn ofwel dat de omtrek = 5,196r. Je zou ook voor het gemak kunnen schrijven dat de omtrek = 5,196r/2 = 2,598d, aangezien d ( =2r ) de middellijn van de cirkel is. Dit rekent wat eenvoudiger.
br/>Als je een vierkant neemt en deze in een cirkel plaatst, dan geldt, dat één zijde ervan = r√2, zodat de vier zijden van het vierkant samen 4r√2r zijn of in d uitgedrukt: 2,828d. Bij een regelmatige vijfhoek blijkt de omtrek hiervan 2,94d te zijn. Ga je nog verder met regelmatige veelhoeken als een zeshoek, een achthoek, een tienhoek, een twaalfhoek, een vierentwintighoek, een zesendertighoek, een tweeënzeventighoek, een driehonderdzestighoek, een zevenhondertwintighoek, tot een zesendertighonderdhoek, dan blijkt, dat naarmate het aantal hoeken groter wordt, de constante nadert naar het getal 3,14159..Voor het gemak is men deze wiskundige constante maar π gaan noemen.
Uit deze eenvoudige benadering blijkt, dat in het begin de constante vrij snel stijgt, maar dat na een 72-hoek de stijging nog maar gering is. Het constante getal 3,14….. gaat hierna langzaam naderen tot het ons bekende getal π, waarbij er steeds meer decimalen bijkomen. Vergelijking met de cirkelboogUit de tabel blijkt al, dat naarmate het aantal hoeken van de veelhoek groter wordt, het constante getal π steeds meer in zicht komt. Dit houdt ook in, dat elk rechte lijnstukje van de veelhoek dat op de cirkel ligt, steeds meer op een cirkelboogje gaat lijken, waardoor
uiteindelijk de zijden van de veelhoek samenvallen met de cirkelbogen.
Bij een tweeënzeventighoek is, zoals de tabel laat zien, de constante al aardig op weg naar de wiskundige constante π.
Het irrationale getal πIn wiskundige termen uitgedrukt, is de wiskundige constante π is een irrationaal getal , dat zelfs transcendent is. Dit houdt in dat π niet als een verhouding van twee hele getallen te schrijven is en dat in de decimale voorstelling geen zich herhalend patroon voorkomt. De waarde van π kan daarom in decimale notatie alleen benaderd worden, want de reeks cijfers achter de komma is oneindig lang.
|
