Karakteristiek

In de abstracte algebra is de karakteristiek van een ring R het kleinste aantal keren dat men in een som gebruik moet maken van het multiplicatieve identiteitselement (1) om het additieve identiteitselement (0) te verkrijgen; van de ring zegt men dat deze karakteristiek nul heeft, indien deze herhaalde som nooit de additieve identiteit bereikt.

Formele definitie

Zij R een ring (niet noodzakelijk commutatief) met neutraal element 1_R voor de vermenigvuldiging. De karakteristiek van R, genoteerd char(R), is het kleinste natuurlijke getal getal n zodanig dat:

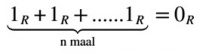
als een dergelijk getal n bestaat, en anders 0.

Voorbeelden

hebben in de klassieke getallenverzamelingen de karakteristiek 0. Zo ook de p-adische getallen.

Als R een integriteitsgebied is - dat wil zeggen dat er geen elementen a,b ϵ R \ {0} bestaan met a • b = 0 – dan is de karakteristiek 0 of een priemgetal. Dit geldt in het bijzonder als R een lichaam (in België: veld) is, - dat wil zeggen dat er geen elementen a,b ϵ R \ {0} bestaan met a . b = 0 – dan is de karakteristiek 0 of een priemgetal.
De gehele restklassen modulo n (n = 2,3,4,…) vormen een commutatieve ring met eenheid met karakteristiek n, genoteerd: / n . Dit is een lichaam, als en slechts als n een priemgetal is.
Als R₁ en R₂ ringen met eenheid zijn, en R₁ is een deelring van R₂ ( met het zelfde eenheidselement ), dan hebben R₁ en R₂ dezelfde karakteristiek. Omgekeerd: elke ring met karakteristiek O bevat als deelring, en elke ring met karakteristiek n >1 bevat /n als deelring.
De enige ring met karakteristiek 1 is het singleton { 0 = 1 }.

Alternatieve definities

De karakteristiek is gelijk aan de exponent van de additieve groep van de ring, dat wil zeggen, de kleinste positieve n zodanig dat:

voor elk element a van de ring (nogmaals, als n bestaat, anders nul). Dit volgt uit de distributiviteit van de vermenigvuldiging ten opzichte van de optelling. Andere equivalente definities nemen de karakteristiek als het natuurlijk getal n zodanig dat n de kern van een ringhomomorfisme van naar R is, zodanig, dat R een deelring isomorf met de factorring /n bevat, die de afbeelding van dat homomorfisme zou worden. De eisen van ringhomomorfismen zijn zodanig, dat er slechts een homomorfisme van de ring van de gehele getallen naar enig andere ring kan zijn. In de taal van categorietheorie is het initiële object van de categorie van ringen. Ook hier volgt men de conventie, dat een ring een multiplicatief identiteitselement heeft, en dat ring-homoformismen het eenheidselement respecteren.