Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Gebruiker:Franciscus/kladblok 2: verschil tussen versies
Geen bewerkingssamenvatting |
Geen bewerkingssamenvatting |
||
| Regel 1: | Regel 1: | ||
=Over het minimum en maximum van een kegel= | =Over het minimum en het maximum van een kegel= | ||
Wat merk je op, als je op een veld in Zeeland - vlakbij de Oosterschelde - een aantal kegelvormige, stroachtige gewassen aantreft, afgedekt met zeildoek? | Wat merk je op, als je op een veld in Zeeland - vlakbij de Oosterschelde - een aantal kegelvormige, stroachtige gewassen aantreft, afgedekt met zeildoek? | ||
De een zal er even naar kijken, en daarna gewoon verder lopen. De ander zal wat meer belangstelling tonen en wat meer daar van willen weten. | De een zal er even naar kijken, en daarna gewoon verder lopen. De ander zal wat meer belangstelling tonen en wat meer daar van willen weten. | ||
Versie van 8 okt 2016 11:49
Over het minimum en het maximum van een kegel
Wat merk je op, als je op een veld in Zeeland - vlakbij de Oosterschelde - een aantal kegelvormige, stroachtige gewassen aantreft, afgedekt met zeildoek? De een zal er even naar kijken, en daarna gewoon verder lopen. De ander zal wat meer belangstelling tonen en wat meer daar van willen weten.


De gewassen bleken bloemzaden te zijn, die aan de lucht worden gedroogd. Het is een oude, maar nog steeds efficiënte manier van drogen.
Al kijkend naar deze opstellingen, kwam de herinnering aan een onderwerp naar boven, waar de schrijver van dit essay ooit een artikel over maakte, namelijk dat een kegel een zeer bijzondere eigenschap bezit.
Het blijkt namelijk, dat bij het groter of kleiner worden van de straal R – bij een gegeven inhoud V - niet alleen het oppervlak A groter of kleiner wordt, maar dat ook een kleinste oppervlak aanwezig is, of met andere woorden:
Het oppervlak bereikt een limiet bij wijziging van de straal en de hoogte.
Deze stelling vraag natuurlijk om een nadere toelichting.
Oppervlak en inhoud van de kegel

Een Kegel is een ruimtelijke figuur, en bestaat uit een plat en een gekromd vlak. Het platte vlak is de bodem in de vorm van een cirkel. Het gekromde vlak is de mantel van de kegel.
Voor de berekening van de inhoud V en het oppervlak A zijn de hoogte h en de straal 'R' nodig.
De afmetingen van kegelvormige opstellingen op het veld waren ongeveer als volgt:
R = 0,5 m en h = 0,9 m.
( Om het rekenen met al te grote of te kleine getallen te vermijden, worden de meters vervangen door decimeters:
1 dm = 0,1 m = 10 -1 m
br/>De inhoud V en het oppervlak A van een kegel worden uitgedrukt in de volgende formules:
Minimum en maximum
Zoals in de inleiding al werd opgemerkt, blijkt bij een kegel bij een constant blijvende inhoud V en variëren van de straal R een kleinste oppervlak A tevoorschijn te komen. Hier gebeurt dit, door de oorspronkelijke straal R = 5 dm van de kegel te variëren, waardoor steeds andere oppervlakken ontstaan, waaronder een minimum oppervlak. Dat leidt tot het inzicht, dat van alle kegels met inhoud V = 235,6 dm 3 er maar één kegel voldoet aan deze eigenschap.
Voor het berekenen van het wisselende oppervlak A is het noodzakelijk de daarbij behorende hoogte h te weten. Deze kan worden berekend uit de inhoud V , namelijk:
In bijgaande tabel zijn de resultaten van de bijbehorende berekeningen opgenomen.
| Straal R ( dm ) | Hoogte h ( dm ) | Oppervlak A ( dm 2 ) |
|---|---|---|
| 1 | 225 | 710 |
| 1,5 | 100 | 491 |
| 2 | 56,24 | 366 |
| 2,5 | 36,3 | 305 |
| 3 | 25,0 | 265,6 |
| 3,5 | 18,36 | 243,98 |
| 4 | 14,06 | 234,0 |
| 4,5 | 11,11 | 233 |
| 5 | 9,03 | 240,6 |
| 5,5 | 7,437 | 254,8 |
| 6 | 6,27 | 276,7 |
| 6,5 | 5,325 | 304 |
| 7 | 4,61 | 338,2 |
| 7,5 | 4,0 | 377 |
| 8 | 3,53 | 420,83 |
| 8,5 | 3,1139 | 468,7 |
| 9 | 2,7775 | 521 |
| 9,5 | 2,493 | 577 |
| 10 | 2,2498 | 636 |
| 10,5 | 2,04 | 700 |
Kijkend naar de resultaten van de berekeningen, wordt het al snel duidelijk, dat het kleinste oppervlak A aanwezig is bij een straal R = 4,5 dm.
, zoals uit de tabel blijkt.
In de grafische voorstelling komt dit fenomeen nog duidelijker naar voren.
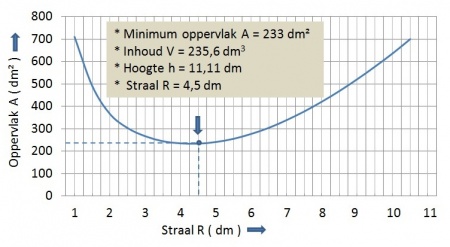
Uit de grafiek en uit de tabel blijkt duidelijk, dat:
- naarmate R groter wordt dan de gegeven afmeting, zal de kegel steeds meer naar een platte schijf naderen
- naarmate h groter wordt dan de gegeven afmeting, zal de kegel steeds meer naar een slanke cilinder naderen.
Nadere beschouwing
Uit de berekeningen van de kegelvormige opstellingen op het land, kan worden vastgesteld, dat bij deze ongeveer het minimum oppervlak aanwezig is. Voor het drogen van het gewas lijkt dit minder geschikt te zijn. Aan de andere kant is het ook niet eenvoudig hier van af te wijken, hoewel met een redelijk eenvoudige wijziging al een redelijke verbetering zal optreden. Als bijvoorbeeld van een straal R = 5 dm wordt overgegaan op een straal R = 7 dm, dan neemt het oppervlak A al met ca 40% toe en bij R = 9 dm leidt dit al tot meer dan een verdubbeling. Hetzelfde geldt voor verkleining van de straal R tot bijvoorbeeld 2,5 dm. Dit levert een bijna 30% groter oppervlak A op. Deze optie heeft bovendien nog het voordeel, dat bij regen het gewas wat minder nat zal worden.
Nawoord
De simpele waarneming van een aantal kegelvormige, stroachtige gewassen heeft geleid tot een nadere beschouwing, waarbij gebleken is, dat een kegel bij een constante inhoud V en bij wijziging van de straal R, het oppervlak A groter of kleiner wordt. Het blijkt verder dat dit stijgen en dalen van het oppervlak A uitmondt in een minimum oppervlak, of anders geformuleerd:
- Het oppervlak A van een kegel nadert een limiet bij wijziging van de straal R en de hoogte h.
Over het minimum en maximum van een kegel
Wat merk je op, als je op een veld in Zeeland - vlakbij de Oosterschelde - een aantal kegelvormige, stroachtige gewassen aantreft, afgedekt met zeildoek? De een zal er even naar kijken, en daarna gewoon verder lopen. De ander zal wat meer belangstelling tonen en wat meer daar van willen weten.


De gewassen bleken bloemzaden te zijn, die aan de lucht worden gedroogd. Het is een oude, maar nog steeds efficiënte manier van drogen.
Al kijkend naar deze opstellingen, kwam de herinnering aan een onderwerp naar boven, waar de schrijver van dit essay ooit een artikel over maakte, namelijk dat een kegel een zeer bijzondere eigenschap bezit.
Het blijkt namelijk, dat bij het groter of kleiner worden van de straal R – bij een gegeven inhoud V - niet alleen het oppervlak A groter of kleiner wordt, maar dat ook een kleinste oppervlak aanwezig is, of met andere woorden:
Het oppervlak bereikt een limiet bij wijziging van de straal en de hoogte.
Deze stelling vraag natuurlijk om een nadere toelichting.
Oppervlak en inhoud van de kegel

Een Kegel is een ruimtelijke figuur, en bestaat uit een plat en een gekromd vlak. Het platte vlak is de bodem in de vorm van een cirkel. Het gekromde vlak is de mantel van de kegel.
Voor de berekening van de inhoud V en het oppervlak A zijn de hoogte h en de straal 'R' nodig.
De afmetingen van kegelvormige opstellingen op het veld waren ongeveer als volgt:
R = 0,5 m en h = 0,9 m.
( Om het rekenen met al te grote of te kleine getallen te vermijden, worden de meters vervangen door decimeters:
1 dm = 0,1 m = 10 -1 m
br/>De inhoud V en het oppervlak A van een kegel worden uitgedrukt in de volgende formules:
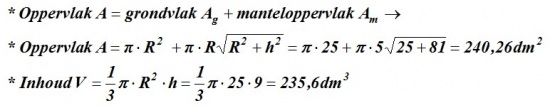
Minima en maxima
Zoals in de inleiding al werd opgemerkt, blijkt bij een kegel bij een constant blijvende inhoud V en variëren van de straal R een kleinste oppervlak A tevoorschijn te komen. Hier gebeurt dit, door de oorspronkelijke straal R = 5 dm van de kegel te variëren, waardoor steeds andere oppervlakken ontstaan, waaronder een minimum oppervlak. Dat leidt tot het inzicht, dat van alle kegels met inhoud V = 235,6 dm 3 er maar één kegel voldoet aan deze eigenschap.
Voor het berekenen van het wisselende oppervlak A is het noodzakelijk de daarbij behorende hoogte h te weten. Deze kan worden berekend uit de inhoud V , namelijk:

In bijgaande tabel zijn de resultaten van de bijbehorende berekeningen opgenomen.
| Straal R ( dm ) | Hoogte h ( dm ) | Oppervlak A ( dm 2 ) |
|---|---|---|
| 1 | 225 | 710 |
| 1,5 | 100 | 491 |
| 2 | 56,24 | 366 |
| 2,5 | 36,3 | 305 |
| 3 | 25,0 | 265,6 |
| 3,5 | 18,36 | 243,98 |
| 4 | 14,06 | 234,0 |
| 4,5 | 11,11 | 233 |
| 5 | 9,03 | 240,6 |
| 5,5 | 7,437 | 254,8 |
| 6 | 6,27 | 276,7 |
| 6,5 | 5,325 | 304 |
| 7 | 4,61 | 338,2 |
| 7,5 | 4,0 | 377 |
| 8 | 3,53 | 420,83 |
| 8,5 | 3,1139 | 468,7 |
| 9 | 2,7775 | 521 |
| 9,5 | 2,493 | 577 |
| 10 | 2,2498 | 636 |
| 10,5 | 2,04 | 700 |
Kijkend naar de resultaten van de berekeningen, wordt het al snel duidelijk, dat het kleinste oppervlak A aanwezig is bij een straal R = 4,5 dm.
, zoals uit de tabel blijkt.
In de grafische voorstelling komt dit fenomeen nog duidelijker naar voren.

Uit de grafiek en uit de tabel blijkt duidelijk, dat:
- naarmate R groter wordt dan de gegeven afmeting, zal de kegel steeds meer naar een platte schijf naderen
- naarmate h groter wordt dan de gegeven afmeting, zal de kegel steeds meer naar een slanke cilinder naderen.
Nadere beschouwing
Uit de berekeningen van de kegelvormige opstellingen op het land, kan worden vastgesteld, dat bij deze ongeveer het minimum oppervlak aanwezig is. Voor het drogen van het gewas lijkt dit minder geschikt te zijn. Aan de andere kant is het ook niet eenvoudig hier van af te wijken, hoewel met een redelijk eenvoudige wijziging al een redelijke verbetering zal optreden. Als bijvoorbeeld van een straal R = 5 dm wordt overgegaan op een straal R = 7 dm, dan neemt het oppervlak A al met ca 40% toe en bij R = 9 dm leidt dit al tot meer dan een verdubbeling. Hetzelfde geldt voor verkleining van de straal R tot bijvoorbeeld 2,5 dm. Dit levert een bijna 30% groter oppervlak A op. Deze optie heeft bovendien nog het voordeel, dat bij regen het gewas wat minder nat zal worden.
Nawoord
De simpele waarneming van een aantal kegelvormige, stroachtige gewassen heeft geleid tot een nadere beschouwing, waarbij gebleken is, dat een kegel bij een constante inhoud V en bij wijziging van de straal R, het oppervlak A groter of kleiner wordt. Het blijkt verder dat dit stijgen en dalen van het oppervlak A uitmondt in een minimum oppervlak, of anders geformuleerd:
- Het oppervlak A van een kegel nadert een limiet bij wijziging van de straal R en de hoogte h.
