Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Verlichting van binnenruimten: verschil tussen versies
Geen bewerkingssamenvatting |
(balast naar sjabloon) |
||
| Regel 89: | Regel 89: | ||
[[Bestand:Verlichtingssterkte in een punt p.jpg|right|275px|Verlichtingssterkte in punt p]] | [[Bestand:Verlichtingssterkte in een punt p.jpg|right|275px|Verlichtingssterkte in punt p]] | ||
Met het gegeven armatuur en het bijbehorende lichtsterktediagram, kan de verlichtingssterkte ''E<sub>p</sub>'' in elk punt ''p'' van een vlak in een constructiewerkplaats worden berekend. Aangezien het lichtsterktediagram voor de aanwezige lichtstroom ''Φ'' is gegeven voor 1000 lumen, moet bij een afwijkende waarde eerst een correctie worden uitgevoerd, aldus: | Met het gegeven armatuur en het bijbehorende lichtsterktediagram, kan de verlichtingssterkte ''E<sub>p</sub>'' in elk punt ''p'' van een vlak in een constructiewerkplaats worden berekend. Aangezien het lichtsterktediagram voor de aanwezige lichtstroom ''Φ'' is gegeven voor 1000 lumen, moet bij een afwijkende waarde eerst een correctie worden uitgevoerd, aldus: | ||
:{|style | :{|{{math style}} | ||
|rowspan="2"|I<sub>p</sub> = | |rowspan="2"|I<sub>p</sub> = | ||
| I · Φ | | I · Φ | ||
| Regel 99: | Regel 99: | ||
Volgens de eerder genoemde formule is: | Volgens de eerder genoemde formule is: | ||
:{|style | :{|{{math style}} | ||
|rowspan="2"|E<sub>p</sub> = | |rowspan="2"|E<sub>p</sub> = | ||
|style="border-bottom: 1px solid black;"|I | |style="border-bottom: 1px solid black;"|I | ||
| Regel 117: | Regel 117: | ||
Als het armatuur ''1 m'' boven het vlak hangt, wordt, aangezien de lichtsterkte bij ''0<sup>o</sup> = 240 cd,'' de verlichtingssterkte: | Als het armatuur ''1 m'' boven het vlak hangt, wordt, aangezien de lichtsterkte bij ''0<sup>o</sup> = 240 cd,'' de verlichtingssterkte: | ||
:{|style | :{|{{math style}} | ||
|rowspan="2"|E<sub>p</sub> = | |rowspan="2"|E<sub>p</sub> = | ||
|style="border-bottom: 1px solid black;"| 1,38 · 240 | |style="border-bottom: 1px solid black;"| 1,38 · 240 | ||
| Regel 127: | Regel 127: | ||
''331 lux'', aangezien de lichtbundel onder een hoek ''α = 30<sup>o</sup>'' uit het armatuur komt, waarbij ''I<sub>p'</sub>'' gedaald is tot 210 cd. Verder wordt bij een hoek α de afstand r tot het vlak vergroot, en wel als volgt: | ''331 lux'', aangezien de lichtbundel onder een hoek ''α = 30<sup>o</sup>'' uit het armatuur komt, waarbij ''I<sub>p'</sub>'' gedaald is tot 210 cd. Verder wordt bij een hoek α de afstand r tot het vlak vergroot, en wel als volgt: | ||
:{|style | :{|{{math style}} | ||
|rowspan="2"|rˊ = | |rowspan="2"|rˊ = | ||
|style="border-bottom: 1px solid black;"|r | |style="border-bottom: 1px solid black;"|r | ||
| Regel 136: | Regel 136: | ||
Aangezien de lichtbundel niet loodrecht op het vlak valt, moet nog een keer met de cosinus van hoek ''α'' worden gerekend, waardoor de verlichtingssterkte in ''p’'' dan wordt: | Aangezien de lichtbundel niet loodrecht op het vlak valt, moet nog een keer met de cosinus van hoek ''α'' worden gerekend, waardoor de verlichtingssterkte in ''p’'' dan wordt: | ||
:{|style | :{|{{math style}} | ||
|rowspan="2"|E<sub>p</sub> = | |rowspan="2"|E<sub>p</sub> = | ||
|style="border-bottom: 1px solid black;"| 1,38 · 210 · cos(30<sup>0</sup>)<sup>3</sup> | |style="border-bottom: 1px solid black;"| 1,38 · 210 · cos(30<sup>0</sup>)<sup>3</sup> | ||
| Regel 145: | Regel 145: | ||
Als algemene formule dus: | Als algemene formule dus: | ||
:{|style | :{|{{math style}} | ||
|rowspan="2"|E<sub>p</sub> = | |rowspan="2"|E<sub>p</sub> = | ||
|style="border-bottom: 1px solid black;"| I<sub>p</sub> · 210 · (cos α)<sup>3</sup> | |style="border-bottom: 1px solid black;"| I<sub>p</sub> · 210 · (cos α)<sup>3</sup> | ||
| Regel 226: | Regel 226: | ||
De vormindex van de ruimte is gelijk aan: | De vormindex van de ruimte is gelijk aan: | ||
:{|style | :{|{{math style}} | ||
|rowspan="2"|k = | |rowspan="2"|k = | ||
|style="border-bottom: 1px solid black;"|l · b | |style="border-bottom: 1px solid black;"|l · b | ||
| Regel 234: | Regel 234: | ||
In ons rekenvoorbeeld is ''k'' dus: | In ons rekenvoorbeeld is ''k'' dus: | ||
:{|style | :{|{{math style}} | ||
|rowspan="2"|k = | |rowspan="2"|k = | ||
|style="border-bottom: 1px solid black;"|7,5 · 4 | |style="border-bottom: 1px solid black;"|7,5 · 4 | ||
| Regel 243: | Regel 243: | ||
In een tabel – behorend bij het gekozen armatuur – kan het verlichtingsrendement (''v'') worden opgezocht, in dit geval 0,41. Er wordt rekening gehouden met een geringe vervuiling en een jaarlijkse reiniging van de armaturen, waardoor een depreciatiefactor ''d'' = 0,9 mag worden aangehouden. Met deze gegevens kan nu het aantal armaturen worden berekend: | In een tabel – behorend bij het gekozen armatuur – kan het verlichtingsrendement (''v'') worden opgezocht, in dit geval 0,41. Er wordt rekening gehouden met een geringe vervuiling en een jaarlijkse reiniging van de armaturen, waardoor een depreciatiefactor ''d'' = 0,9 mag worden aangehouden. Met deze gegevens kan nu het aantal armaturen worden berekend: | ||
:{|style | :{|{{math style}} | ||
|rowspan="2"|E<sub>gem</sub> = | |rowspan="2"|E<sub>gem</sub> = | ||
|style="border-bottom: 1px solid black;"|φ | |style="border-bottom: 1px solid black;"|φ | ||
| Regel 252: | Regel 252: | ||
Hieruit is af te leiden, dat het aantal armaturen ''n'' wordt: | Hieruit is af te leiden, dat het aantal armaturen ''n'' wordt: | ||
:{|style | :{|{{math style}} | ||
|rowspan="2"|n = | |rowspan="2"|n = | ||
|style="border-bottom: 1px solid black;"|E<sub>gem</sub> · A | |style="border-bottom: 1px solid black;"|E<sub>gem</sub> · A | ||
| Regel 260: | Regel 260: | ||
In het rekenvoorbeeld is dit dus: | In het rekenvoorbeeld is dit dus: | ||
:{|style | :{|{{math style}} | ||
|rowspan="2"|n = | |rowspan="2"|n = | ||
|style="border-bottom: 1px solid black;"|500 · 7,5 · 4 | |style="border-bottom: 1px solid black;"|500 · 7,5 · 4 | ||
| Regel 269: | Regel 269: | ||
Dit aantal wordt naar boven afgerond tot 6 armaturen. In nieuwe toestand is de verlichtingssterkte ''E'<sub>gem</sub>'' dan: | Dit aantal wordt naar boven afgerond tot 6 armaturen. In nieuwe toestand is de verlichtingssterkte ''E'<sub>gem</sub>'' dan: | ||
:{|style | :{|{{math style}} | ||
|rowspan="2"|E'<sub>gem</sub> = | |rowspan="2"|E'<sub>gem</sub> = | ||
|style="border-bottom: 1px solid black;"|E<sub>gem</sub> | |style="border-bottom: 1px solid black;"|E<sub>gem</sub> | ||
Versie van 11 mei 2016 16:24
Een goede verlichting moet de zekerheid geven, dat mensen onder alle omstandigheden naar behoren kunnen functioneren en moet bijdragen aan het welzijn van mensen. Verder moet een goede verlichting de veiligheid op de werkplek bevorderen. Voor dat doel is een bepaalde verlichtingssterkte nodig.
Richtwaarden voor een goede verlichting
Om enig inzicht te krijgen hoe groot de verlichtingssterkte ongeveer dient te zijn, geeft bijgaande tabel een indicatie welke verlichtingssterkten voor de diverse werkzaamheden en ruimten gelden.
In de verlichtingsnorm NEN – EN 12464-1 worden de nadere eisen genoemd die bij het ontwerp van een verlichtingsinstallatie in acht genomen moeten worden.
| Aard van de verlichting | Soort ruimte | Standaard- verlichtingssterkte (lux) |
|---|---|---|
| Oriëntatieverlichting | Opslagruimten, parkeergarages, hotelingangen Gangen, trappenhuizen, liften, badkamers, kerkruimten, zalen, foyers |
50 à 100 100 à 200 |
| Werkverlichting | Grof constructiewerk, magazijnen, huiskamers, beurzen, tentoonstellingen Kantoren, leslokalen, montagewerk, keukens, supermarkten Tekenkamers, fijn montagewerk |
200 à 375 400 à 750 800 à 1500 |
| Speciale werkverlichting | Precisiewerk met fijne details Inspectiewerk, operatietafels |
1600 à 3000 3200 à 6000 |
Nederlandse verlichtingsnorm
De nieuwe verlichtingsnorm NEN – EN 12464-1 gaat, zoals gezegd, uitvoeriger in op de verlichting van werkplekken. De norm geeft verlichtingseisen voor werkplekken binnenshuis, die tegemoetkomen aan de behoeften aan visueel comfort en visuele prestatie. Alle gebruikelijke visuele taken zijn in de norm in aanmerking genomen, ook het werken met beeldschermen.
Eenheden en formules
Voor de verlichtingssterkte geldt de volgende definitie:
- De verlichtingssterkte E is de hoeveelheid licht die op een bepaald oppervlak terechtkomt, en wordt uitgedrukt in de eenheid lux. Deze eenheid wordt als volgt gedefinieerd: 1 lux is de lichtsterkte voortgebracht door 1 candela op een oppervlak loodrecht op de lichtstralen op een afstand van 1 meter van de bron.
Naast de grootheden verlichtingssterkte en lichtsterkte, komen ook de lichtstroom Φ en de ruimtehoek ω aan de orde.
In de tabel zijn de diverse grootheden, eenheden en formules overzichtelijk gerangschikt.
| Grootheid | Eenheid | Symbool | Formule |
|---|---|---|---|
| Lichtstroom Lichtsterkte Ruimtehoek |
lumen (lm) candela (cd) steradiaal (sr) |
Φk I ω |
|
| Verlichtingssterkte in een punt
Afstand tot het te verlichten vlak |
lux
m |
Ep
r |
|
| Gemiddelde verlichtingssterkte
Oppervlak |
lux
m2 |
Egem
A |
Polair lichtsterktediagram
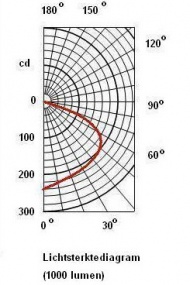
Een armatuur dat een lichtbron bevat, heeft als voornaamste functie het verspreiden of het richten van een lichtbundel naar het te verlichten vlak. De plaats van de lichtbron in dat armatuur, en de vorm en de afwerking bepalen verder de manier waarop een lichtbundel wordt uitgestraald.
De vorm van de lichtbundel is vastgelegd in een zogenaamd polair lichtsterktediagram, dat karakteristiek is voor elk armatuur. Een lichtsterktediagram geeft weer, hoe in een ruimte de lichtsterkteverdeling is onder een bepaalde hoek. De ruimtelijkheid hiervan kan worden voorgesteld, door het diagram langs de verticale as te wentelen over een hoek van 360o, waardoor een tolvormig, ruimtelijk lichaam ontstaat.
Opgemerkt dient te worden, dat een polair diagram geldt voor 1000 lumen. Als een lichtbron meer of minder dan 1000 lumen uitstraalt, dan moet daarvoor een correctie worden uitgevoerd.
Van het afgebeelde gloeilamparmatuur is het bijbehorende polaire diagram gegeven. In een rekenvoorbeeld zal worden ingegaan op de berekening van de verlichtingssterkte volgens de lichtpuntmethode. Bij deze methode wordt uitgegaan van een lichtbundel die op een zeer klein vlak terechtkomt.
Berekening volgens de puntmethode
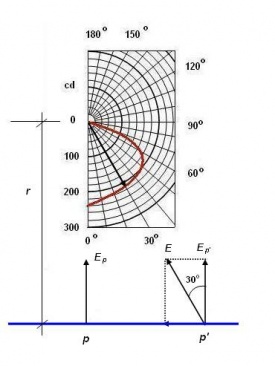
Met het gegeven armatuur en het bijbehorende lichtsterktediagram, kan de verlichtingssterkte Ep in elk punt p van een vlak in een constructiewerkplaats worden berekend. Aangezien het lichtsterktediagram voor de aanwezige lichtstroom Φ is gegeven voor 1000 lumen, moet bij een afwijkende waarde eerst een correctie worden uitgevoerd, aldus:
Ip = I · Φ cd 1000
Als in dit geval een gloeilamp van 100 watt is toegepast, dan moet - aangezien hiervan de lichtstroom Φ bij 230 V = 1380 lumen is - in dit geval de uitkomst worden gecorrigeerd met een factor 1380/1000 = 1,38. Volgens de eerder genoemde formule is:
Ep = I lux r2
Wegens de eerder genoemde correctie wordt dit:
Ep = 1,38 · I lux r2
Als het armatuur 1 m boven het vlak hangt, wordt, aangezien de lichtsterkte bij 0o = 240 cd, de verlichtingssterkte:
Ep = 1,38 · 240 331 lux 12
De verlichtingssterkte in bijvoorbeeld punt p’, wordt kleiner dan 331 lux, aangezien de lichtbundel onder een hoek α = 30o uit het armatuur komt, waarbij Ip' gedaald is tot 210 cd. Verder wordt bij een hoek α de afstand r tot het vlak vergroot, en wel als volgt:
rˊ = r cos α
Aangezien de lichtbundel niet loodrecht op het vlak valt, moet nog een keer met de cosinus van hoek α worden gerekend, waardoor de verlichtingssterkte in p’ dan wordt:
Ep = 1,38 · 210 · cos(300)3 188 lux r2
Als algemene formule dus:
Ep = Ip · 210 · (cos α)3 lux r2
| Hoek α (graden) |
Lichtsterkte I (candela) |
Verlichtings- sterkte Ep (lux) |
|---|---|---|
| 0 | 240 | 331 |
| 10 | 220 | 290 |
| 20 | 218 | 250 |
| 30 | 210 | 188 |
| 40 | 205 | 127 |
| 50 | 200 | 73 |
| 60 | 180 | 31 |
| 70 | 100 | 6 |
Bij een tophoek van 70o, waar de lichtstroom I in het polaire diagram naar 0 nadert, blijkt de verlichtingssterkte Ep’’ nog maar 6 lux te bedragen. Voorts zijn de verlichtingssterkten bij 80o en 90o zo klein, dat ze verwaarloosd kunnen worden.
De berekende verlichtingssterkten Ep van 0o tot 70o kunnen nu overzichtelijk in een tabel worden geplaatst. (Zie rechts.)
Het berekenen van de verlichtingssterkte op de verschillende plaatsen vraagt in de praktijk tamelijk veel rekenwerk. Sommige leveranciers van armaturen verstrekken daarom soms tabellen met verlichtingssterkten voor diverse lichtbronnen met de daarbij behorende hoogten. Met deze tabellen kan op eenvoudige wijze de verlichtingssterkte in elk punt p worden afgelezen.
Gelijkmatigheid
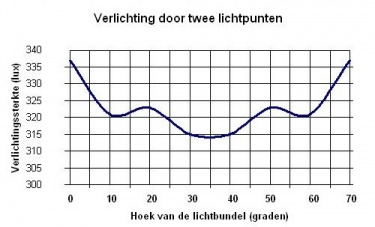 | |||||||||||||||||||||||||||
|
Het zal duidelijk zijn, dat een dergelijke, uiteenliggende verlichtingssterkte op een vlak niet bijdraagt aan het algemene comfort. Alleen direct onder de lamp onder een hoek van 0o blijkt de verlichtingssterkte aan de gestelde eisen te voldoen.
Er wordt nu nog eenzelfde armatuur geplaatst, precies op de plek waar E minimaal is, dus bij α = 70o, wat overeenkomt met een afstand van 2,75 m vanaf het eerste armatuur. De nu aanwezige twee verlichtingssterkten kunnen dan worden opgeteld, wat als bijzonder resultaat oplevert, dat over de gehele afstand de verlichtingssterkte bijna constant is.
In de praktijk lukt het niet altijd zo’n hoge gelijkmatigheid te bereiken. Een gelijkmatigheid van 70% wordt meestal nog als acceptabel beschouwd.
De manier van opstellen van armaturen die elkaar aanvullen, wordt ook vaak toegepast bij de openbare verlichting van bijvoorbeeld autowegen, waarbij meestal een verlichtingssterkte van 20 tot 40 lux wordt aangehouden.
Lichtstroommethode
Voor de verlichting van kantoren, woonhuizen, fabrieken en andere gebouwen, maakt men gebruik van berekeningen volgens de zogenaamde lichtstroommethode. Bij het berekenen volgens deze methode bepaalt de gemiddelde verlichtingssterkte Egem het aantal en de soort armaturen die nodig zijn in een bepaalde ruimte. Daarnaast zijn er nog enkele factoren die moeten worden meegenomen in de berekening, als armatuurrendement η, de verhouding van lengte, breedte en hoogte van de ruimte, uitgedrukt in de vormindex k, de reflectiefactor r van plafond, wanden en vloer, aangezien een deel van het licht wordt geabsorbeerd. Verder is er ook nog de zogenaamde depriciatiefactor d. Er zijn namelijk invloeden die het rendement van een armatuur na een bepaalde tijd omlaag brengen, zoals veroudering van de lichtbron en vervuiling van de lichtbron en de wanden.
Berekeningen volgens de lichtstroommethode
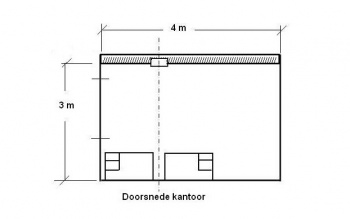
Als voorbeeld van een berekening volgens de lichtstroommethode, is een kantoor gekozen, waarbij de gewenste verlichtingssterkte Egem 500 lux moet zijn. Als armaturen zijn gekozen: direct met lichtrooster TL 36 W, kleur 830 met twee lampen. De lichtstroom Ø van één lamp blijkt 3850 lumen te bedragen.
De armaturen die in een systeemplafond worden opgenomen, moeten evenwijdig aan de raamgevel lopen. De acht bureaus worden met de lengteas loodrecht op deze raamgevel geplaatst.
De afmetingen van het kantoor bedragen: lengte (l) = 7,5 m en breedte (b) = 4 m. De afstand tussen vloer en plafond is 3 m. Het werkvlak ligt op 0,8 m boven de vloer, waardoor de afstand tussen werkvlak en plafond (h) op 2,2 m uitkomt. De reflectiefactor r van het plafond wordt op 0,7 gesteld en van de wanden op 0,5.
De vormindex van de ruimte is gelijk aan:
k = l · b h · (l + b)
In ons rekenvoorbeeld is k dus:
k = 7,5 · 4 2,2 · (7,5 + 4)
In een tabel – behorend bij het gekozen armatuur – kan het verlichtingsrendement (v) worden opgezocht, in dit geval 0,41. Er wordt rekening gehouden met een geringe vervuiling en een jaarlijkse reiniging van de armaturen, waardoor een depreciatiefactor d = 0,9 mag worden aangehouden. Met deze gegevens kan nu het aantal armaturen worden berekend:
Egem = φ A
Hieruit is af te leiden, dat het aantal armaturen n wordt:
n = Egem · A φ · v · d
In het rekenvoorbeeld is dit dus:
n = 500 · 7,5 · 4 = 5,28 armaturen 7700 · 0,41 · 0,9
Dit aantal wordt naar boven afgerond tot 6 armaturen. In nieuwe toestand is de verlichtingssterkte E'gem dan:
E'gem = Egem · 6 = 631 lux d 5,28
De lengte van één armatuur = 1,2 m. De gekozen 6 armaturen passen dus goed in de ruimte, namelijk 6 × 1,2 = 7,2 m.
Bij controleren op eventuele verblindingshinder door een te grote lichtintensiteit (luminantie), blijkt dat deze opstelling aan de vereisten voldoet. De gelijkmatigheid van deze verlichtingsinstallatie ligt op 78%, zodat dit ook binnen de gestelde eisen ligt.
De verlichtingssterkte zal lager zijn op het looppad naast de bureaus dan op de werkvlakken, maar dit levert geen problemen op.
