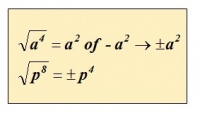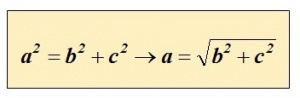Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Algebra ( Machtsverheffen en Worteltrekken ): verschil tussen versies
(Wikificatie) |
|||
| Regel 1: | Regel 1: | ||
Na Algebra ( Vermenigvuldigen en Delen ) komen - zoals in de Rekenkunde - de begrippen '''Machtsverheffen''' en '''Worteltrekken''' aan de orde. | Na Algebra ( Vermenigvuldigen en Delen ) komen - zoals in de Rekenkunde - de begrippen '''Machtsverheffen''' en '''Worteltrekken''' aan de orde. | ||
==Machtsverheffen== | |||
Machtsverheffen gaat op dezelfde manier als bij het rekenen, namelijk: | Machtsverheffen gaat op dezelfde manier als bij het rekenen, namelijk: | ||
:*De cijfers worden vermenigvuldigd | :*De cijfers worden vermenigvuldigd | ||
| Regel 31: | Regel 31: | ||
<br/> | <br/> | ||
<br/> | <br/> | ||
==Worteltrekken== | |||
In Algebra ( 3 ) werd al aangegeven, dat bij het vermenigvuldigen van positieve en negatieve getallen er twee mogelijkheden zijn, namelijk: | In Algebra ( 3 ) werd al aangegeven, dat bij het vermenigvuldigen van positieve en negatieve getallen er twee mogelijkheden zijn, namelijk: | ||
:* Bij ''gelijke'' tekens is de uitkomst '''positief''' | :* Bij ''gelijke'' tekens is de uitkomst '''positief''' | ||
| Regel 54: | Regel 55: | ||
<br/> | <br/> | ||
==Algebra in formules== | |||
Als voorbeeld, hoe Algebra in formules wordt toegepast, geldt de volgende - door bijna iedereen herkende - uitspraak. Een zeer bekende stelling in de wiskunde is namelijk de ''Stelling van Pythagoras''. | Als voorbeeld, hoe Algebra in formules wordt toegepast, geldt de volgende - door bijna iedereen herkende - uitspraak. Een zeer bekende stelling in de wiskunde is namelijk de ''Stelling van Pythagoras''. | ||
<br/>Deze luidt: | <br/>Deze luidt: | ||
| Regel 70: | Regel 71: | ||
==Links== | ==Links== | ||
[[ Algebra ( Algemene regels )]] | * [[ Algebra ( Algemene regels )]] | ||
* [[Algebra ( Optellen en Aftrekken )]] | |||
* [[Algebra ( Vermenigvuldigen en Delen )]] | |||
* [[Algebra ( Vergelijkingen )]] | |||
* [[Algebra ( Merkwaardige producten )]] | |||
[[Categorie:Algebra]] | [[Categorie:Algebra]] | ||
[[Categorie:Wiskunde]] | [[Categorie:Wiskunde]] | ||
Huidige versie van 10 nov 2019 om 19:09
Na Algebra ( Vermenigvuldigen en Delen ) komen - zoals in de Rekenkunde - de begrippen Machtsverheffen en Worteltrekken aan de orde.
Machtsverheffen
Machtsverheffen gaat op dezelfde manier als bij het rekenen, namelijk:
Als het grondtal positief is, dan is het product ook positief:
Als het grondtal negatief is, dan is het product:
- Negatief als de exponent buiten de haakjes oneven is
- Positief als de exponent buiten de haakjes even is

Worteltrekken
In Algebra ( 3 ) werd al aangegeven, dat bij het vermenigvuldigen van positieve en negatieve getallen er twee mogelijkheden zijn, namelijk:
- Bij gelijke tekens is de uitkomst positief
- Bij ongelijke tekens is de uitkomst negatief
Dat houdt dus in, dat als bijvoorbeeld de wortel uit 64 wordt getrokken, de uitkomst twee mogelijkheden heeft, namelijk: 8 of - 8.
Dit wordt als volgt aangegeven: ± 8.
.
Bij algebraïsche bewerkingen gaat dit op precies dezelfde manier:
Algebra in formules
Als voorbeeld, hoe Algebra in formules wordt toegepast, geldt de volgende - door bijna iedereen herkende - uitspraak. Een zeer bekende stelling in de wiskunde is namelijk de Stelling van Pythagoras.
Deze luidt:
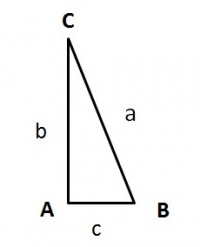
In een rechthoekige driehoek is de som van de kwadraten van de rechthoekszijden gelijk aan het kwadraat van de schuine zijde.
Dit houdt in, dat als van een rechthoekige driehoek twee zijden bekend zijn, met behulp van de stelling van Pythagoras de derde zijde kan worden berekend.
De stelling kan met de rechthoekige driehoek ABC en de bijbehorende rechthoekszijden a,b en c in de vorm van een formule worden uitgedrukt, namelijk: