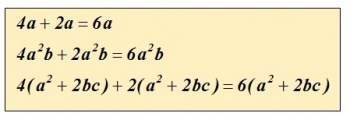Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Algebra ( Optellen en Aftrekken ): verschil tussen versies
Geen bewerkingssamenvatting |
Geen bewerkingssamenvatting |
||
| Regel 1: | Regel 1: | ||
==Optellen en aftrekken== | |||
In [[Algebra ( Algemene regels )]] werden de regels behandeld, die algemeen gelden in de Algebra. In de volgende alinea's komen '''Optellen''' en '''Aftrekken''' aan de orde. | In [[Algebra ( Algemene regels )]] werden de regels behandeld, die algemeen gelden in de Algebra. In de volgende alinea's komen '''Optellen''' en '''Aftrekken''' aan de orde. | ||
Het optellen en aftrekken in de Algebra gaat bijna op dezelfde manier als in de Rekenkunde. Het enige verschil is, dat de uitkomst steeds in letters blijft, tenzij men de letters door cijfers vervangt. | Het optellen en aftrekken in de Algebra gaat bijna op dezelfde manier als in de Rekenkunde. Het enige verschil is, dat de uitkomst steeds in letters blijft, tenzij men de letters door cijfers vervangt. | ||
<br/>In het eerste voorbeeld zijn enkele termen opgeteld. | <br/>In het eerste voorbeeld zijn enkele termen opgeteld. | ||
Versie van 12 mrt 2014 18:48
Optellen en aftrekken
In Algebra ( Algemene regels ) werden de regels behandeld, die algemeen gelden in de Algebra. In de volgende alinea's komen Optellen en Aftrekken aan de orde.
Het optellen en aftrekken in de Algebra gaat bijna op dezelfde manier als in de Rekenkunde. Het enige verschil is, dat de uitkomst steeds in letters blijft, tenzij men de letters door cijfers vervangt.
In het eerste voorbeeld zijn enkele termen opgeteld.
Het aftrekken gaat ongeveer op dezelfde manier als het optellen, zoals het voorbeeld laat zien.
Bij breuken wordt op een soortgelijke manier gehandeld, alleen moeten de noemers – als deze niet gelijk zijn – worden aangepast. Dit aanpassen gebeurt door kruislings te vermenigvuldigen, aldus :
- de eerste teller met de tweede noemer, daarna delen door de eerste en de tweede noemer
- de tweede teller met de eerste noemer, daarna delen door de eerste en de tweede noemer

Getallen kleiner dan 0
Behalve met letters wordt in de Algebra ook met getallen < 0 gewerkt.
Om bij bewerkingen het onderscheid tussen positieve en negatieve getallen aan te geven, wordt bij de positieve getallen soms een + vóór het getal geplaatst. Meestal is dit echter niet nodig. Bij de negatieve getallen wordt wel altijd een – vóór het getal geplaatst.
Links
Algebra ( Algemene regels )
Algebra ( Vermenigvuldigen en Delen )
Algebra ( Machtsverheffen en Worteltrekken )
Algebra ( Vergelijkingen )
Algebra ( Merkwaardige producten )