Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Magisch vierkant: verschil tussen versies
(Opsommingstekens vervangen door inspringing, omdat een bolletje teveel op een vermenigvuldigingsteken lijkt) |
|||
| Regel 1: | Regel 1: | ||
::''Een magisch vierkant of tovervierkant is een is een ordening van getallen in een vierkant waarin getallen zodanig zijn ingevuld, dat de kolommen, de rijen en de diagonalen alle dezelfde som opleveren.'' | ::''Een magisch vierkant of tovervierkant is een is een ordening van getallen in een vierkant waarin getallen zodanig zijn ingevuld, dat de kolommen, de rijen en de diagonalen alle dezelfde som opleveren.'' | ||
Diezelfde som – een constant getal dus – wordt ook wel de ''magische constante'' genoemd.. | Diezelfde som – een constant getal dus – wordt ook wel de ''magische constante'' genoemd.. | ||
<br/>Magische vierkanten zijn een fascinerende manier om getallen te rangschikken, en zijn zeer in populariteit gegroeid, zeker sinds de opkomst van op wiskunde gebaseerde spelletjes als [[Sudoku]]. | <br/>Magische vierkanten zijn een fascinerende manier om getallen te rangschikken, en zijn zeer in populariteit gegroeid, zeker sinds de opkomst van op wiskunde gebaseerde spelletjes als [[Sudoku]]. | ||
==Oorsprong== | ==Oorsprong== | ||
Magische vierkanten behoren tot de oudst bekende wiskundige objecten. Als voorbeeld dient het beroemde 3 x 3 magische vierkant, wat volgens Chinese legenden uit 2800 voor Christus stamt. Volgens deze legenden, stroomde de rivier Lo geregeld over. Men geloofde dat er offers aan de riviergod gebracht moesten | Magische vierkanten behoren tot de oudst bekende wiskundige objecten. Als voorbeeld dient het beroemde 3 x 3 magische vierkant, wat volgens Chinese legenden uit 2800 voor Christus stamt. Volgens deze legenden, stroomde de rivier Lo geregeld over. Men geloofde dat er offers aan de riviergod gebracht moesten worden om de rivier te kalmeren, maar ieder offer was echter tevergeefs. | ||
worden om de rivier te kalmeren, maar ieder offer was echter tevergeefs. | <br/>Na weer zo’n overstroming merkte een kind op, dat er een schildpad op het land aanspoelde, met negen opmerkelijke tekens op haar schild, in een drie bij drie raster. Op het allereerste gezicht zag men niet echt iets opvallends aan dat vierkant. | ||
<br/>Na weer zo’n overstroming merkte een kind op, dat er een schildpad op het land | |||
aanspoelde, met negen opmerkelijke tekens op haar schild, in | |||
een drie bij drie raster. Op het allereerste gezicht zag men niet echt iets opvallends aan dat vierkant. | |||
<br/>Bij nadere beschouwing bleek echter, dat er '''getallen''' op het schild stonden, en dat de kolommen, de rijen en de diagonalen in het vierkante patroon alle dezelfde som opleverden, namelijk 15. Dit werd als een duidelijke opdracht beschouwd en leidde uiteindelijk tot het brengen van 15 offers aan de riviergod, om de rivier te kalmeren. Het getal '''15''' had nu een zeer speciale betekenis gekregen. | <br/>Bij nadere beschouwing bleek echter, dat er '''getallen''' op het schild stonden, en dat de kolommen, de rijen en de diagonalen in het vierkante patroon alle dezelfde som opleverden, namelijk 15. Dit werd als een duidelijke opdracht beschouwd en leidde uiteindelijk tot het brengen van 15 offers aan de riviergod, om de rivier te kalmeren. Het getal '''15''' had nu een zeer speciale betekenis gekregen. | ||
Dit vierkant werd voortaan '''Lo Shu''' genoemd, wat betekent: '''Boek van de rivier Lo'''. | Dit vierkant werd voortaan '''Lo Shu''' genoemd, wat betekent: '''Boek van de rivier Lo'''. | ||
| Regel 18: | Regel 16: | ||
==Variaties== | ==Variaties== | ||
[[Afbeelding:Lo 2.jpg|250px|centre]] | [[Afbeelding:Lo 2.jpg|250px|centre]] | ||
Elk magisch vierkant met drie velden kan worden verkregen uit het Lo Shu vierkant door rotatie of spiegeling. Er zijn namelijk op het Lo Shu vierkant enkele variaties mogelijk. Door kanteling van de rijen verschuiven deze, maar blijft de magische constante = 15 gelijk. | Elk magisch vierkant met drie velden kan worden verkregen uit het Lo Shu vierkant door rotatie of spiegeling. Er zijn namelijk op het Lo Shu vierkant enkele variaties mogelijk. Door kanteling van de rijen verschuiven deze, maar blijft de magische constante = 15 gelijk. | ||
==Middeleeuwen== | ==Middeleeuwen== | ||
Ook de Europeanen raakten geïnteresseerd in de magische vierkanten uit het Oosten. Tot de zestiende eeuw werden de magische vierkanen hier nog beschouwd als figuren met toverkracht. Ze werden gebruikt voor het bezweren van geesten. | Ook de Europeanen raakten geïnteresseerd in de magische vierkanten uit het Oosten. Tot de zestiende eeuw werden de magische vierkanen hier nog beschouwd als figuren met toverkracht. Ze werden gebruikt voor het bezweren van geesten. | ||
<br/>In de eeuw van de verlichting werden magische vierkanten de geliefkoosde onderwerpen van de rekenkunstenaars en wiskundigen. Een uit die tijd bekend magisch vierkant komt voor op de gravure Melencolia I (melancholie) van Albrecht Dürer <sup>1)</sup> uit 1514. | <br/>In de eeuw van de verlichting werden magische vierkanten de geliefkoosde onderwerpen van de rekenkunstenaars en wiskundigen. Een uit die tijd bekend magisch vierkant komt voor op de gravure Melencolia I (melancholie) van Albrecht Dürer <sup>1)</sup> uit 1514. | ||
[[Afbeelding: Dürer Melancholia.jpg|450px|left]] | [[Afbeelding: Dürer Melancholia.jpg|450px|left]] | ||
[[Afbeelding:Vierkant Albrecht Dürer.jpg|350px|right]] | [[Afbeelding:Vierkant Albrecht Dürer.jpg|350px|right]] | ||
| Regel 51: | Regel 50: | ||
Als klassiek voorbeeld uit die tijd werd ''n'' = 4 gekozen. Het constante getal van dit vierkant is volgens de geldende rekenkundige reeks: | Als klassiek voorbeeld uit die tijd werd ''n'' = 4 gekozen. Het constante getal van dit vierkant is volgens de geldende rekenkundige reeks: | ||
::''<big>1/2n( n<sup>2</sup> + 1 )</big>'' | |||
waarbij ''n'' = aantal velden | waarbij ''n'' = aantal velden | ||
| Regel 57: | Regel 56: | ||
Ingevuld wordt dit voor ''n'' = 4: | Ingevuld wordt dit voor ''n'' = 4: | ||
::''<big>2( n<sup>2</sup> + 1 ) = 34 | |||
</big>'' | </big>'' | ||
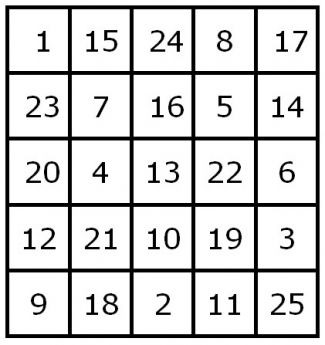
[[Afbeelding:4 x 4.jpg|300px|centre]] | [[Afbeelding:4 x 4.jpg|300px|centre]] | ||
Op de afbeelding is het magische vierkant uit de berekening te zien. Duidelijk is, dat de magische constanten van de rijen en de kolommen en van de twee diagonalen allemaal = 34 zijn, en dat de som van het gehele vierkant volgens de hiervoor geldende rekenkundige reeks: | Op de afbeelding is het magische vierkant uit de berekening te zien. Duidelijk is, dat de magische constanten van de rijen en de kolommen en van de twee diagonalen allemaal = 34 zijn, en dat de som van het gehele vierkant volgens de hiervoor geldende rekenkundige reeks: | ||
::''<big> ½ a( n<sup>2</sup> + 1 ) = 136</big>'' | |||
waarbij ''a'' = alle vierkantjes van het magisch vierkant zijn. | waarbij ''a'' = alle vierkantjes van het magisch vierkant zijn. | ||
| Regel 71: | Regel 70: | ||
Er zijn nog meer bijzonderheden in het magisch vierkant aanwezig. Als namelijk het vierkant wordt verdeeld in vier vakken, dan is de som van die vier getallen ook steeds 34. | Er zijn nog meer bijzonderheden in het magisch vierkant aanwezig. Als namelijk het vierkant wordt verdeeld in vier vakken, dan is de som van die vier getallen ook steeds 34. | ||
:::::::::''( 16 + 3 + 10 + 5 = 34,'' enz ) | :::::::::''( 16 + 3 + 10 + 5 = 34,'' enz.) | ||
==Verdere mogelijkheden== | ==Verdere mogelijkheden== | ||
| Regel 77: | Regel 76: | ||
Hierbij is de magische constante: | Hierbij is de magische constante: | ||
::''<big>1/2 n( n<sup>2</sup> + 1 )</big>'' = ''<big>2,5( 26 ) = 65, | |||
</big>'' | </big>'' | ||
en de som van alle getallen: | en de som van alle getallen: | ||
::''<big>½ a( n<sup>2</sup> + 1 ) = 12,5( 26 ) = 325 | |||
</big>'' | </big>'' | ||
Ook bij dit magische vierkant zijn allerlei variaties mogelijk. | Ook bij dit magische vierkant zijn allerlei variaties mogelijk. | ||
Naarmate het aantal velden ''n'' toeneemt, wordt namelijk ook het aantal variaties groter. Er zijn zelfs | Naarmate het aantal velden ''n'' toeneemt, wordt namelijk ook het aantal variaties groter. Er zijn zelfs magische vierkanten, die driedimensionaal zijn. | ||
<br/>Het voert te ver om hier nader op in te gaan. | <br/>Het voert te ver om hier nader op in te gaan. | ||
{{Bron|bronvermelding= | {{Bron|bronvermelding= | ||
:*Geraadpleegde literatuur: Diverse bronnen en '''Quadrivium''', Rekenkunde, Meetkunde, Muziek en Astronomie voor iedereen. Librero, ISBN | :*Geraadpleegde literatuur: Diverse bronnen en '''Quadrivium''', Rekenkunde, Meetkunde, Muziek en Astronomie voor iedereen. Librero, ISBN 978-90-8998-303-9 | ||
:*Zie ook: [[Magische ring]] | :*Zie ook: [[Magische ring]] | ||
:* <sup>1)</sup> Albrecht Dürer (21 mei 1471 | :* <sup>1)</sup> Albrecht Dürer (21 mei 1471 – 6 april 1528), was een Duits kunstschilder, tekenaar, maker van houtsneden en kopergravures, kunsttheoreticus en humanist uit de Noordelijke renaissance, en had kennis van de wiskunde. | ||
}} | }} | ||
[[Categorie: Rekenkunde]] | [[Categorie: Rekenkunde]] | ||
Versie van 18 mrt 2019 07:36
- Een magisch vierkant of tovervierkant is een is een ordening van getallen in een vierkant waarin getallen zodanig zijn ingevuld, dat de kolommen, de rijen en de diagonalen alle dezelfde som opleveren.
Diezelfde som – een constant getal dus – wordt ook wel de magische constante genoemd..
Magische vierkanten zijn een fascinerende manier om getallen te rangschikken, en zijn zeer in populariteit gegroeid, zeker sinds de opkomst van op wiskunde gebaseerde spelletjes als Sudoku.
Oorsprong
Magische vierkanten behoren tot de oudst bekende wiskundige objecten. Als voorbeeld dient het beroemde 3 x 3 magische vierkant, wat volgens Chinese legenden uit 2800 voor Christus stamt. Volgens deze legenden, stroomde de rivier Lo geregeld over. Men geloofde dat er offers aan de riviergod gebracht moesten worden om de rivier te kalmeren, maar ieder offer was echter tevergeefs.
Na weer zo’n overstroming merkte een kind op, dat er een schildpad op het land aanspoelde, met negen opmerkelijke tekens op haar schild, in een drie bij drie raster. Op het allereerste gezicht zag men niet echt iets opvallends aan dat vierkant.
Bij nadere beschouwing bleek echter, dat er getallen op het schild stonden, en dat de kolommen, de rijen en de diagonalen in het vierkante patroon alle dezelfde som opleverden, namelijk 15. Dit werd als een duidelijke opdracht beschouwd en leidde uiteindelijk tot het brengen van 15 offers aan de riviergod, om de rivier te kalmeren. Het getal 15 had nu een zeer speciale betekenis gekregen.
Dit vierkant werd voortaan Lo Shu genoemd, wat betekent: Boek van de rivier Lo.
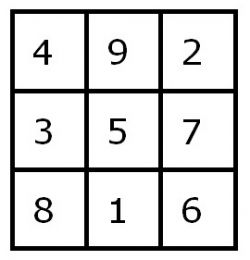
De magische constante van dit Lo Shu vierkant = 15, waarbij het cijfer 1 aan de onderkant en de 2 in de rechterbovenhoek aanwezig is. De som van alle getallen in het vierkant = 45.
Het Lo Shu vierkant wordt in astrologische kringen ook wel het Saturnesvierkant genoemd.
Dit vierkant heeft nog een hogere magische eigenschap, namelijk: 42 + 92 + 2 2 = 82+ 12 + 62 =101, en
42 + 32 + 82 = 22 + 72 + 62 = 89.
Variaties
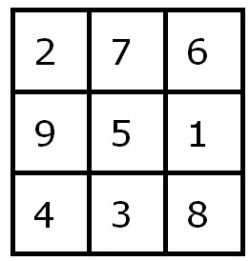
Elk magisch vierkant met drie velden kan worden verkregen uit het Lo Shu vierkant door rotatie of spiegeling. Er zijn namelijk op het Lo Shu vierkant enkele variaties mogelijk. Door kanteling van de rijen verschuiven deze, maar blijft de magische constante = 15 gelijk.
Middeleeuwen
Ook de Europeanen raakten geïnteresseerd in de magische vierkanten uit het Oosten. Tot de zestiende eeuw werden de magische vierkanen hier nog beschouwd als figuren met toverkracht. Ze werden gebruikt voor het bezweren van geesten.
In de eeuw van de verlichting werden magische vierkanten de geliefkoosde onderwerpen van de rekenkunstenaars en wiskundigen. Een uit die tijd bekend magisch vierkant komt voor op de gravure Melencolia I (melancholie) van Albrecht Dürer 1) uit 1514.


- Merk op, dat het jaartal van de gravure verwerkt zit in de onderste rij van het vierkant.
Door de wiskundigen werd gesteld, dat een magisch vierkant een vierkant is, dat als een dambord verdeeld is in n2 velden. In die n2 velden zet men de getallen 1, 2,... n2 zodanig, dat zij zowel horizontaal als verticaal, maar ook in de diagonalen steeds dezelfde som geven.
Als klassiek voorbeeld uit die tijd werd n = 4 gekozen. Het constante getal van dit vierkant is volgens de geldende rekenkundige reeks:
- 1/2n( n2 + 1 )
waarbij n = aantal velden
Ingevuld wordt dit voor n = 4:
- 2( n2 + 1 ) = 34
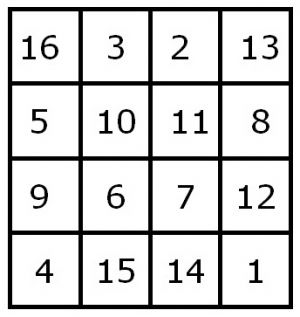
Op de afbeelding is het magische vierkant uit de berekening te zien. Duidelijk is, dat de magische constanten van de rijen en de kolommen en van de twee diagonalen allemaal = 34 zijn, en dat de som van het gehele vierkant volgens de hiervoor geldende rekenkundige reeks:
- ½ a( n2 + 1 ) = 136
waarbij a = alle vierkantjes van het magisch vierkant zijn.
Extra eigenschappen
Ook bij dit vierkant zijn enkele variaties mogelijk. Door kanteling van de rijen verschuiven deze, maar blijft de magische constante gelijk = 34.
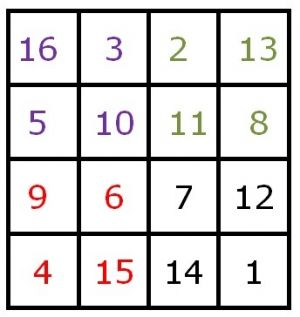
Er zijn nog meer bijzonderheden in het magisch vierkant aanwezig. Als namelijk het vierkant wordt verdeeld in vier vakken, dan is de som van die vier getallen ook steeds 34.
- ( 16 + 3 + 10 + 5 = 34, enz.)
Verdere mogelijkheden
De gegeven vierkanten zijn het begin van een reeks magische vierkanten, die steeds ingewikkelder worden. Zo is het eerstvolgende magische vierkant een vierkant met n = 52 velden.
Hierbij is de magische constante:
- 1/2 n( n2 + 1 ) = 2,5( 26 ) = 65,
en de som van alle getallen:
- ½ a( n2 + 1 ) = 12,5( 26 ) = 325
Ook bij dit magische vierkant zijn allerlei variaties mogelijk.
Naarmate het aantal velden n toeneemt, wordt namelijk ook het aantal variaties groter. Er zijn zelfs magische vierkanten, die driedimensionaal zijn.
Het voert te ver om hier nader op in te gaan.
Bronvermelding
Bronnen, noten en/of referenties:
- Geraadpleegde literatuur: Diverse bronnen en Quadrivium, Rekenkunde, Meetkunde, Muziek en Astronomie voor iedereen. Librero, ISBN 978-90-8998-303-9
- Zie ook: Magische ring
- 1) Albrecht Dürer (21 mei 1471 – 6 april 1528), was een Duits kunstschilder, tekenaar, maker van houtsneden en kopergravures, kunsttheoreticus en humanist uit de Noordelijke renaissance, en had kennis van de wiskunde.
