Wikisage is op 1 na de grootste internet-encyclopedie in het Nederlands. Iedereen kan de hier verzamelde kennis gratis gebruiken, zonder storende advertenties. De Koninklijke Bibliotheek van Nederland heeft Wikisage in 2018 aangemerkt als digitaal erfgoed.
- Wilt u meehelpen om Wikisage te laten groeien? Maak dan een account aan. U bent van harte welkom. Zie: Portaal:Gebruikers.
- Bent u blij met Wikisage, of wilt u juist meer? Dan stellen we een bescheiden donatie om de kosten te bestrijden zeer op prijs. Zie: Portaal:Donaties.
Algebra ( Merkwaardige producten ): verschil tussen versies
Geen bewerkingssamenvatting |
Geen bewerkingssamenvatting |
||
| Regel 1: | Regel 1: | ||
==Merkwaardige producten== | |||
Na Algebra ( Vergelijkingen ) komen in dit laatste lemma over Algebra enkele belangrijke '''Merkwaardige Producten''' aan de orde. | Na Algebra ( Vergelijkingen ) komen in dit laatste lemma over Algebra enkele belangrijke '''Merkwaardige Producten''' aan de orde. | ||
<br/>Merkwaardige producten worden soms toegepast om diverse bewerkingen ''gemakkelijk'' en ''snel'' te kunnen uitvoeren. | |||
Merkwaardige producten worden | |||
<br/>De vorm bestaat uit twee delen, namelijk: | <br/>De vorm bestaat uit twee delen, namelijk: | ||
:* het ''merkwaardige product'' en de'' uitwerking'' daarvan. | :* het ''merkwaardige product'' en de'' uitwerking'' daarvan. | ||
Versie van 12 mrt 2014 18:51
Merkwaardige producten
Na Algebra ( Vergelijkingen ) komen in dit laatste lemma over Algebra enkele belangrijke Merkwaardige Producten aan de orde.
Merkwaardige producten worden soms toegepast om diverse bewerkingen gemakkelijk en snel te kunnen uitvoeren.
De vorm bestaat uit twee delen, namelijk:
- het merkwaardige product en de uitwerking daarvan.
Enkele veel gebruikte merkwaardige producten zijn:
Er zijn nog enkele andere merkwaardige producten, en zelfs Merkwaardige Quotiënten, maar deze worden minder toegepast.
Een voorbeeld van hoe met een merkwaardig product een schijnbaar moeilijke vermenigvuldiging op een eenvoudige manier uit het hoofd kan worden opgelost, is deze:
Een andere, directe toepassing van merkwaardige producten is de volgende.
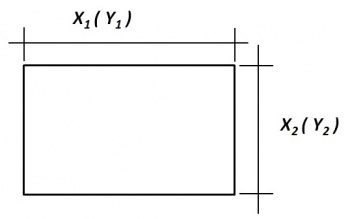
In Algebra ( Vergelijkingen ) werden met behulp van de vierkantsvergelijking de twee zijden van een rechthoek berekend.
Het oplossen van dit vraagstuk, kan ook met behulp van een merkwaardig product.
Door omzetting kan worden bepaald, dat:
Afsluiting
Met de behandeling van de Merkwaardige Producten wordt het vak Algebra afgesloten.
Zoals in Algebra ( Algemene regels ) in het begin al werd opgemerkt, wordt het vak Algebra vaak toegepast bij technische vraagstukken die ingewikkelde beredeneringen met zich meebrengen en daardoor vaak tot lange becijferingen met grote getallen leiden. Met Algebra wordt vaak het gecompliceerde karakter van deze berekeningen weggehaald.
Getracht is het vak Algebra voor geïnteresseerden toegankelijk te maken, door de stof stapsgewijs te behandelen en met veel voorbeelden te werken
Links
Algebra ( Algemene regels )
Algebra ( Optellen en Aftrekken )
Algebra ( Vermenigvuldigen en Delen )
Algebra ( Machtsverheffen en Worteltrekken )
Algebra ( Vergelijkingen )